Основное уравнение гидростатики

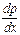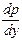Из уравнений (II, 15) следует, что давление в покоящейся жидкости изменяется только по вертикали (вдоль оси z, рис. II-2), оставаясь одина­ковым во всех точках любой горизонтальной плоскости, так как изменения давлений вдоль осей х и у равны нулю. В связи с тем, что в этой системе уравнений частные производные и равны нулю, частная произ­водная 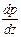может быть заменена на 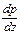и, следовательно

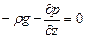
Отсюда

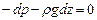(II,16)

Разделив левую и правую части последнего выражения на pg и пере­менив знаки, представим это уравнение в виде

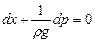
Для несжимаемой однородной жидкости плотность постоянна и, сле­довательно

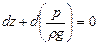
или

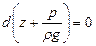
откуда после интегрирования получим

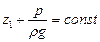(II,17)

Для двух произвольных горизонтальных плоскостей 1 и 2 уравне­ние (II,17) выражают в форме

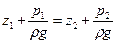(II,18)

Уравнение (II,17) пли (II,18) является основным уравне­нием гидростатики.

В уравнении (II,18): z₁ и z₂ — высоты расположения двух точек внутри покоящейся однородной капельной жидкости над произвольно выбранной горизонтальной плоскостью отсчета (плоскостью сравнения), а р₁ и p₂ — гидростатические давления в этих точках.

Рассмотрим, например, две частицы жидкости, из которых одна рас­положена в точке 1 внутри объема жидкости (рис. II-3) — на высоте z от произвольно выбранной плоскости сравнения 0-0, а другая находится в точ­ке 2 на поверхности жидкости — на вы­соте x_o от той же плоскости. Пусть р и p_o — давления в точках 1 и 2 соответст­венно.

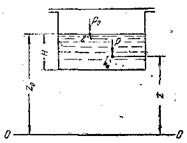
Рис. II-3. К основному уравнению гидростатики

При этих обозначениях, согласно уравнению (II,18)

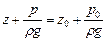(II,18а)

или

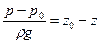(II,18б)

Член z в уравнении гидростатики [уравнение (II,17)], представляющий собой высоту расположения данной точки над произвольно выбранной плоскостью сравнения, называется нивелирной высотой. Она, как и другой член этого уравнения, выражается в единицах длины

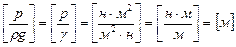
Величину 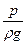называют напором давления, или пьезо­метрическим напором.

Следовательно, согласно основному уравнению гидростатики, для каждой точки покоящейся жидкости сумма нивелирной высоты и пьезометрического напора есть величина постоянная.

Члены основного уравнения гидростатики имеют определенный энергетический смысл. Так, выражение члена 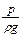до сокращения 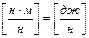характеризует удельную энергию, т.е. энергию, приходящуюся на единицу веса жидкости 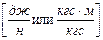. Аналогичный энергетический смысл получает и нивелирная высота, если ее выраже­ние [м] умножить и затем разделить на единицу веса жидкости.

Таким образом, нивелирная высота z, называемая также геометри­ческим (высотным) напором, характеризует удельную потенциальную энергию положения данной точки над выбранной плоскостью сравнения (см. рис. II-3), а пьезометрический на­пор — удельную потенциальную энергию давле­ния в этой точке. Сумма указанных энергий, называемая полным гидростатическим напором, или просто статическим напором, равна общей потенциальной энергии, приходящейся на единицу веса жидкости.

Следовательно, основное уравнение гидростатики представляет собой частный случай закона сохранения энергии: удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.

Уравнение (II,18а) можно записать и в форме

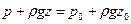(II,18в)

или

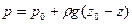(II,18г)

Последнее уравнение является выражением закона Паскаля, согласно которому давление, создаваемое в любой точке покоящейся несжи­маемой жидкости, передается одинаково всем точкам ее объема. Действи­тельно, в соответствии с уравнением (II,18г), при любом изменении дав­ления р₀ в точке z₀ давление р во всякой другой точке жидкости изменится настолько же.