Некоторые физические свойства жидкостей

Рассмотрим некоторые физические свойства жидкостей и параметры, используемые при расчете процессов химической технологии, протекаю­щих в покоящейся или движущейся жидкости.

Плотность и удельный вес. Масса единицы объема жидкости назы­вается плотностью и обозначается через r:

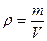(II,1)

где m — масса жидкости; V — объем жидкости.

В единицах СИ плотность измеряется в кг/м², а в системе МКГСС, где масса выражается в кгс×сек²/м, единица плотности будет кгс×сек²/м⁴.

Вес единицы объема жидкости называется удельным весом и обозначается через g, т. е.

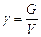(II,2)

В единицах СИ удельный вес измеряется в н/м³, а в системе МКГСС, где единицей веса является кгс, — кгс/м³.

Масса и вес связаны между собой соотношением

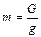
где g — ускорение свободного падения, м/сек².

Подставив это значение m в зависимость (II,1), с учетом выраже­ния (II,2) получим соотношение между удельным весом и плотностью:

g=rg (II,3)

Плотность и удельный вес капельных жидкостей значительно выше, чем соответствующие характеристики упругих жидкостей (газов) и сравни­тельно мало изменяются под действием давления или при изменении тем­пературы. Плотность газов с большей или меньшей степенью точности может быть рассчитана на основе уравнения состояния для идеальных газов:

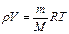(II,4)

где при использовании единиц СИ и соответствующем выражении давления r в н/м², тем­пературы Т в °К и массы 1 кмоль (мольной массы) газа М в кг/кмоль универсальная газовая постоянная равна R = 8314 дж/(кмоль×град).

Из уравнения (II,4) следует, что

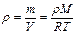(II,5)

Объем, занимаемый единицей массы газа, или величина, обратная плотности, называется удельным объемом и обозначается через n:

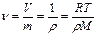(II,6)

Давление. Жидкость оказывает давление на дно и стенки сосуда, в ко­тором она находится, и на поверхность любого погруженного в нее тела. Рассмотрим некоторую элементарную площадку F внутри объема покоя­щейся жидкости. Независимо от положения площадки в данной точке объема жидкость будет давить на нее с некоторой силой, равной Р и направленной по нормали к площадке, на которую она действует. Ее на­зывают силой гидростатического давления. Отноше­ние P/F представляет собой среднее гидростатическое давление, а предел этого отношения при F®0 носит название гид­ростатического давления в точке, или просто давления:

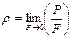(II,7)

Через каждую точку внутри жидкости может проходить бесконечно большое число элементарных площадок. При этом сила Р в любой точке направлена по нормали к каждой такой площадке, на которую она действует. Иначе эту силу можно было бы разложить на нормальную и параллельную плоскости площадки составляющие, и параллельная со­ставляющая вызвала бы перемещение слоев жидкости, что невозможно, так как по условию жидкость находится в покое. Давление в любой точке жидкости одинаково по всем направлениям, поскольку в противном случае также происходило бы перемещение жидкости внутри занимаемого ею объема.

Из определения давления следует, что его единица в СИ выражается в н/м², а в системе единиц МКГСС— в кгс/м².

В расчетах давление часто выражают также в физических и техниче­ских атмосферах или в единицах высоты Н столба манометрической жид­кости (воды, ртути и др.).

Между давлением, выраженным в н/м² (или в кгс/м²) и в единицах вы­соты столба жидкости, существует простая связь:

r = gH = rgH (II,8)

В соответствии с этим можно установить следующие соотношения между различными единицами давления:

1 атмосфера физическая (1 атм) = 760 мм рт. ст. = 10,33 м вод. ст. = 1,033 кгс/см² = 10 330 кгс/м² = 101 300 н/м²;

1 атмосфера техническая (1 ат) = 735,6 мм рт. ст. = 10 м вод. ст. = 1 кгс/см² = 10 000 кгс/м² = 98 100 н/м².

Приборы для измерения давления (манометры или вакуумметры) по­казывают не абсолютное давление р_абс внутри замкнутого объема, а разность между абсолютным и атмосферным, или барометрическим, дав­лением р_атм. Эту разность называют избыточным давлением р_изб, если давление в объеме превышает атмосферное, и разрежением р_разр, если оно ниже атмосферного (в системе вакуум). Таким образом

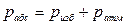(II,9)

и

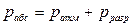(II,10)

Вязкость. При движении реальной жидкости в ней возникают силы внутреннего трения, оказывающие сопротивление движению. Эти силы действуют между соседними слоями жидкости, перемещающимися друг относительно друга. Свойство жидкости оказывать сопротивление усилиям, вызывающим относительное перемещение ее частиц, называется вяз­костью.

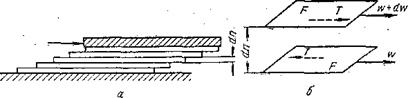
Рис. II-1. К характеристике вязкости.

Представим себе слой жидкости, находящийся между двумя параллель­ными горизонтальными пластинами (рис. II-1, а). Для того чтобы пере­мещать верхнюю пластину относительно нижней в горизонтальной пло­скости с постоянной скоростью, нужно прилагать некоторую постоянную касательную силу, т.к. вязкая жидкость оказывает сопротивление такому перемещению. Соответственно в жидкости при наличии указанного перемещения возникнут, и будут существовать касательные напряжения между отдельными ее слоями. Весь слой жидкости, расположенной между пластинами, при этом можно представить состоящим из бесконечно боль­шого числа элементарных слоев толщиной dn каждый. Очевидно, напря­жения сдвига будут возникать, между любыми соседними элементарными слоями вследствие трения между ними вдоль поверхности соприкоснове­ния слоев. На рис. II-1, б представлены два таких параллельных слоя площадью F каждый, причем расположенный выше слой движется со скоростью (w + dw), большей, чем скорость расположенного ниже слоя, на бесконечно малую величину dw.

Опыт показывает, что касательная сила Т, которую надо прилагать к верхнему слою для его равномерного сдвига относительно нижнего (или противоположно направленная сила трения Т, с которой нижний слой сопротивляется перемещению верхнего), тем больше, чем больше градиент скорости 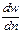, характеризующий изменение скорости, при­ходящееся на единицу расстояния по нормали между слоями. Кроме того, каждая из сил Т пропорциональна площади соприкосновения F слоев. Следовательно

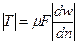(II, 11)

где m — коэффициент пропорциональности, характерный для данной жидкости.

Отношение величины |T| к поверхности соприкосновения слоев обо­значают через t и называют напряжением внутреннего трения, а также напряжением сдвига, или касатель­ным напряжением. Соответственно уравнение (II,11) принимает вид

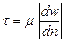(II, 12)

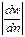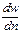Так как величина t всегда положительна, то знак перед правой частью уравнения, включающего не , а , зависит от знака градиента скорости. Условимся во всех случаях проводить нормаль я к поверхности F соприкосновения перемещающихся относительно друг друга слоев жид­кости в направлении уменьшения скорости (рис, II,1). Тогда градиент скорости всегда будет отрицательным, и уравнение (II, 12) преобразуется к виду

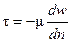(II, 12a)

Уравнение (II, 12), или (II, 12а), выражает закон внутрен­него трения Ньютона, согласно которому напряжение внутрен­него трения, возникающее между слоями жидкости при ее течении, прямо пропорционально градиенту скорости.

Знак минус в правой части уравнения (II, 12а) в соответствии с выше­изложенным, указывает на то, что касательное напряжение тормозит слой, движущийся с относительно большей скоростью (или разгоняет относи­тельно медленно движущийся слой). Другое обоснование выражения закона Ньютона уравнением (II, 12а) дано несколько ниже при рассмотрении еще одного физического смысла этого закона.

Коэффициент пропорциональности m в уравнениях (II, 11), или (II,12), называется динамическим коэффициентом вязкости, динамической вязкостью, или просто вязкостью.

Вязкость в СИ выражается следующим образом:

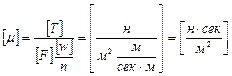
а в системе СГС

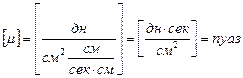
В справочной литературе значения вязкости часто приводятся не в пуа­зах (пз), а в сантипуазах (спз), равных 0,01 пз.

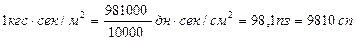
Соотношение между единицами вязкости в системах единиц СИ и СГС:

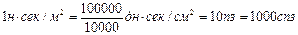
Соотношение между технической единицей вязкости и единицами вяз­кости в системе СГС:

Иногда вязкость жидкостей характеризуют кинематическим коэффициентом вязкости, или кинематической вязкостью:

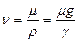(II,13)

Единицей кинематической вязкости в системе СГС является стокс (cm), равный 1 см²/сек, или 100 сантистоксам (сст), В системах СИ и МКГСС единица кинематической вязкости равна 1 м²/сек = 10⁴ ст.

Вязкость капельных жидкостей колеблется в широких пределах. Так, при комнатной температуре вязкость воды составляет ~1 спз, а вязкость глицерина — около 1500 спз. Вязкость газов значительно ниже: например, вязкость воздуха приблизительно в 50 раз меньше вязкости воды.

Вязкость капельных жидкостей значительно снижается с возрастанием температуры. Вязкость газов, наоборот, увеличивается с ее повышением. При умеренном давлении вязкость газов практически от него не зависит, однако, начиная с некоторого давления, возрастает при его увеличении.

Причины различного влияния температуры на вязкость капельных жидкостей и газов, а также отмеченного характера влияния давления на вязкость последних обусловлены тем, что вязкость газов имеет молекулярно-кинетическую природу, а вязкость капельных жидкостей в основном зависит от сил сцепления между молекулами.

Значения вязкостей капельных жидкостей и газов приводятся в спра­вочной литературе, но могут быть определены также для чистых веществ и их смесей расчетным путем.

Уравнению (II, 12а) можно придать и другой физический смысл. Слой жидкости массой т, примыкающий к перемещаемой верхней пластине (рис. II, 1), приобретает некоторую скорость и, следовательно, коли­чество движения, или импульс (mw), в направлении перемещения. Этот слой приводит в движение следующий, передавая ему некоторую часть импульса, и т.д. — от слоя к слою. Следовательно, при течении жидкости происходит перенос количества движения (импульса) в направлении, перпендикулярном направлению скорости жидкости. Соответственно касательное напряжение t (н/м²) может рассматриваться как удельный поток импульса, или количество движения, передаваемое через единицу площади в единицу времени:

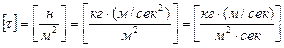
Таким образом, согласно уравнению (II, 12а), удельный поток количества движения прямо пропорционален градиенту скорости,

Знак минус в данном уравнении указывает на то, что перенос коли­чества движения осуществляется в направлении уменьшения скорости (направления потока импульса и возрастания скорости противоположны). Градиент скорости при этом можно считать движущей силой переноса импульса.

Такая интерпретация уравнения (II,12а) позволяет выявить аналогию между переносом механического движения (трения), тепла и массы. Кроме того, она отвечает физическому меха­низму, лежащему в основе закона внутреннего трения. Так, при движении в потоке газа двух соседних элементарных слоев с несколько отличными скоростями (между ними имеется градиент 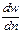), вследствие хаотического движения молекул во всех направлениях, часть их из более быстро дви­жущегося, слоя, попадая в более медленный слой и сталкиваясь с его молекулами, будет ускорять последний. Наоборот, молекулы из более медленного слоя, попадая в более быстрый соседний слой, будут его затормаживать. Обмен молекулами между слоями и вызывает перенос количества движения поперечно скорости слоев, причем для преодоления силы сопротивления между слоями требуется прилагать определенную силу.

Жидкости чаще всего подчиняются закону внутреннего трения Нью­тона. Такие жидкости называют нормальными, или ньютонов­скими. Однако в промышленной практике приходится иметь дело и с неньютоновскими жидкостями, обладающими аномальными свойствами. Не следуют закону Ньютона растворы многих полимеров, коллоидные растворы, густые суспензии, пасты и др.

Вязкость оказывает существенное влияние на режимы течения жидко­стей и на сопротивления, возникающие при их движении. Поэтому интен­сификация многих гидродинамических, а также тепловых и массообменных процессов часто достигается при уменьшении вязкости среды, например путем повышения температуры капельных жидкостей.

Поверхностное натяжение. В ряде процессов химической технологии капельная жидкость при движении соприкасается с газом (или паром) или с другой капельной жидкостью, практически не смешивающейся с первой. Поверхность раздела между фазами стремится к минимуму под действием поверхностных сил. Соответственно капли, взвешенные в газе (паре) или в другой жидкости, и пузырьки газа в жидкости принимают форму, более или менее близкую к шарообразной. Это объясняется тем, что молекулы жидкости внутри ее объема испытывают примерно одинаковое воздействие соседних молекул, в то время как молекулы, находя­щиеся непосредственно у поверхности раздела фаз, притягиваются моле­кулами внутренних слоев жидкости сильнее, чем молекулами окружаю­щей среды. В результате на поверхности жидкости возникает давление, направленное внутрь жидкости по нормали к ее поверхности, которое и стремится уменьшить эту поверхность до минимума.

Следовательно, для увеличения поверхности, т.е. для создания новой поверхности, необходима некоторая затрата энергии. Работу, требуемую для образования единицы новой поверхности, называют межфазным, или поверхностным натяжением и обозначают через s.

Поверхностное натяжение выражается в следующих единицах:

в системе СИ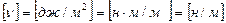

в системе СГС [s] = [эрг/см²] = [дин/см²]

в системе МКГСС [s] = [кгс·м/м²] = [кгс/м]

Из приведенных выражений s следует, что поверхностное натяжение можно рассматривать также как силу, действующую на единицу длины поверхности раздела жидкости и соприкасающейся с ней среды.

Поверхностное натяжение уменьшается с увеличением температуры. С величиной s связаны характеристики смачивания капельными жидко­стями твердых материалов; смачивание оказывает существенное влияние на гидродинамические условия протекания процессов в абсорбционных и ректификационных аппаратах, конденсаторах паров и др.

В справочной литературе обычно приводятся значения поверхностного натяжения на границе жидкость — воздух. Натяжение же, возникающее при соприкосновении несмешивающихся (или частично смешивающихся) капельных жидкостей, называют также граничным натяже­нием. Последнее, как правило, значительно меньше натяжения на гра­нице жидкость-газ. Так, на границе вода-воздух s = 73 дин/см (при 20 °С), а на границе вода-бензол s » 35 дин/см.

Граничное натяжение значительно влияет на диспергирование одной жидкости в другой, с ней не смешивающейся, и поэтому существенно ска­зывается на гидродинамических условиях проведения процессов жидкост­ной экстракции.