Дифференциальные уравнения равновесия Эйлера

В объеме жидкости, находящейся в покое, выделим элементарный параллелепипед объемом dV с ребрами dx, dy и dz, расположенными парал­лельно осям координат х, у и z (рис. II-2). Сила тяжести, действующая на параллелепипед, выражается произведением его массы dm на ускорение свободного падения g, т.е. равна gdm. Сила гидростатического давления на лю­бую из граней параллелепипеда равна произведению гидростатического давления р на площадь этой грани. Будем считать, что давление р является функцией всех трех координат; р = f (x, у, z). Выясне­ние вида этой функции, т.е. закона распределения гидростатического давле­ния по объему жидкости, и является на­шей задачей.

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. В противном случае происходило бы перемещение жидкости.

Рассмотрим сумму проекций сил на ось z. Сила тяжести направлена вниз, параллельно оси z. Поэтому при выбранном положительном направ­лении оси z (см. рис. II-2) сила тяжести будет проектироваться на эту ось со знаком минус:

-gdm = -grdV = - rgdxdydz

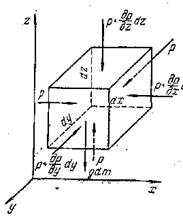
Рис. II-2. К выводу дифференциальных уравнений равновесия Эйлера.

Сила гидростатического давления действует на нижнюю грань парал­лелепипеда по нормали к ней, и ее проекция на ось z равна p dx dy. Если изменение гидростатического давления в данной точке в направлении оси z равно 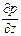, то по всей длине ребра dz оно составит 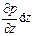. Тогда гидростати­ческое давление на противоположную (верхнюю) грань равно 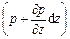и проекция силы гидростатического давления на ось z

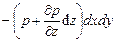
Проекция равнодействующей силы давления на ось z

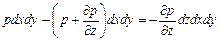
Сумма проекций сил на ось z равна нулю, т.е.

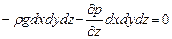(II,14)

или, учитывая, что объем параллелепипеда dxdydz = dV ¹ 0 (величина, заведомо не равная нулю), получим

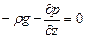
Проекции сил тяжести на оси х и у равны нулю. Поэтому сумма проек­ций сил на ось х

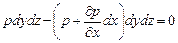
откуда после раскрытия скобок и сокращения находим

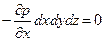(II,14a)

или

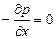
Соответственно для оси у

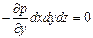
или

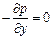
Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:

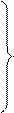
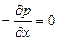
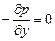(II,15)

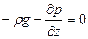
Уравнения (II, 15) представляют собой дифференциальные уравнения равновесия Эйлера.

Для получения закона распределения давления во всем объеме покоя­щейся жидкости следует проинтегрировать систему уравнений (II, 15), Интегралом этих уравнений является основное уравнение гидростатики, широко используемое в инженерной практике.