Общие принципы анализа и расчета процессов и аппаратов

Расчеты процессов и аппаратов обычно имеют следующие основные цели:

а) определение условий предельного, или равновесного, состояния системы;

б) вычисление расходов исходных материалов и количеств полу­чаемых продуктов, а также количеств потребной энергии (тепла) и расхода теплоносителей;

в) определение оптимальных режимов работы и соответствующей им рабочей поверхности или рабочего объема аппаратов;

г) вычисление основных размеров аппаратов.

Эти задачи определяют содержание и последовательность расчетов. Исходным этапом являются расчет и анализ статики процесса, т.е. рассмотрение данных о равновесии, на основе которых определяют направление и возможные пределы осуществления процесса. Пользуясь этими данными, находят предельные значения параметров про­цесса, необходимые для вычисления его движущей силы. Затем составляют материальные и энергетические балансы, исходя из законов сохранения массы и энергии. Последующий этап представляет собой расчет кинетики процесса, определяющей его скорость. По данным о скорости и движущей силе при выбранном оптимальном режиме работы аппарата находят его рабочую поверхность или объем. Зная поверхность или объем, определяют основные размеры аппарата.

Материальный баланс. По закону сохранения массы масса поступаю­щих веществ 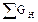должна быть ра₅вна массе веществ 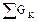, получаемых в результате проведения процесса, т.е. без учета потерь + .

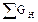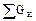Однако в практических условиях неизбежны необратимые потери веществ, обозначая которые через 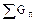находим следующее общее выра­жение материального баланса:

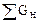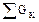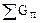= + (I,1)

Материальный баланс составляют для процесса в целом или для отдель­ных его стадий. Баланс может быть составлен для системы в целом или по одному из входящих в нее компонентов. Так, материальный баланс процесса сушки составляют как по всему влажному материалу, поступаю­щему на сушку, так и по одному из его компонентов — массе абсолютно сухого вещества или массе влаги, содержащейся в высушиваемом мате­риале. Баланс составляют либо за единицу времени, например за 1 ч, за сутки (или за одну операцию в периодическом процессе) либо в расчете на единицу массы исходных или конечных продуктов.

На основе материального баланса определяют выход продукта, под которым понимают выраженное в процентах отношение полученного ко­личества (массы) продукта к максимальному, т.е. теоретически возмож­ному.

Иногда понятию выход придают иной смысл, рассчитывая условно выход как массу продукта, отнесенную к единице массы затраченного сырья. При этом в случае использования нескольких видов сырья выход выражают по отношению к какому-либо одному из них. Практический расход исходных материалов обычно превышает теоретический вслед­ствие того, что химические реакции не протекают до конца, происходят потери реагирующих веществ (через неплотности аппаратуры и т.д.).

Энергетический баланс. Этот баланс составляют на основе закона сохра­нения энергии, согласно которому количество энергии, введенной в про­цесс, равно количеству выделившейся энергии, т.е. приход энергии равен ее расходу. Проведение химико-технологических процессов обычно свя­зано с затратой различных видов энергии — механической, электрической и др. Эти процессы часто сопровождаются изменением энтальпии системы, в частности, вследствие изменения агрегатного состояния веществ (испа­рения, конденсации, плавления и т.д.). В химических процессах очень большое значение может иметь тепловой эффект протекающих реакций.

Частью энергетического баланса является тепловой баланс, который в общем виде выражается уравнением

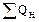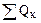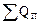= + (I,2)

При этом вводимое тепло

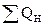= Q₁ + Q₂ + Q₃

где Q₁ — тепло, вводимое с исходными веществами; Q₂ — тепло, подводимое извне, напри­мер с теплоносителем, обогревающим аппарат; Q₃ — тепловой эффект физических или хими­ческих превращений (если тепло в ходе процесса поглощается, то этот член входит с отри­цательным знаком).

Отводимое тепло SQ_к складывается из тепла, удаляющегося с конеч­ными продуктами и отводимого с теплоносителем (например, с охла­ждающим агентом).

В энергетическом балансе, кроме тепла, учитываются приход и расход всех видов энергии, например затраты механической энергии на переме­щение жидкостей или сжатие и транспортирование газов.

На основании теплового баланса находят расход водяного пара, воды и других теплоносителей, а по данным энергетического баланса — общий расход энергии на осуществление процесса.

Интенсивность процессов и аппаратов. Для анализа и расчета процес­сов химической технологии. Необходимо, кроме данных материального и энергетического балансов, знать интенсивность процессов и аппаратов.

Все указанные выше основные процессы (гидродинамические, тепло­вые, массообменные и др.) могут протекать только под действием некоторой движущей силы, которая для гидромеханических процессов определяется разностью давлений, для теплообменных – разностью тем­ператур, для массообменных – разностью концентраций вещества и т.д. Выражения движущей силы для различных видов процессов будут рас­смотрены в соответствующих главах курса.

В первом приближении можно считать, что результат процесса, харак­теризуемый, например, массой М. перенесенного вещества или количеством переданного тепла, пропорционален движущей силе (обозначаемой в общем виде через D), времени t и некоторой величине A, к которой относят интенсивность процесса. Такой величиной может быть рабочая поверхность, через которую происходит перенос энергии или массы, рабочий объем, в котором осуществляется процесс, и т.п. Следовательно, уравнение любого процесса может быть представлено в общем виде:

M = KAtD (I,3)

Коэффициент пропорциональности К в уравнении характеризует скорость процесса и, таким образом, представляет собой кинетический коэффициент, или коэффициент скорости процесса (коэффициент теплопередачи, коэффициент массопередачи и т.д.). Коэффициент К отражает влияние всех факторов, не учтенных величинами, входящими в правую часть уравнения (I,3), а также все отклонения реального процесса от этой упрощенной зависимости.

Под интенсивностью процесса понимают результат его, отнесенный к единице времени и единице величины А, т.е. величину М/Аt, например энергию или массу, перешедшую в единицу времени через единицу рабочей поверхности (либо перенесенной из одной фаз в единице рабочего объема). Из уравнения следует, что

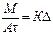(I,4)

Соответственно величину К можно рассматривать как меру интенсив­ности процесса — интенсивность, отнесенную к единице движущей силы.

Интенсивность процесса всегда пропорциональна движу­щей силе D и обратно пропорциональна сопро­тивлению R, которое является величиной, обратной кинетическому коэффициенту (например, гидравлическое сопротивление, термическое сопротивление, сопротивление массопередаче и т.д.). Таким образом, уравнение (I,3) может быть выражено также в форме

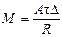(I,5)

Из уравнения (I,3) или (I,5) находят необходимую рабочую поверх­ность или рабочий объем аппарата по известным значениям остальных величин, входящих в уравнение, или определяют результат процесса при заданной поверхности (объеме).

От интенсивности процесса следует отличать объемную интен­сивность аппарата — интенсивность, отнесенную к единице его общего объема. С увеличением объемной интенсивности уменьшаются размеры аппарата, и снижается расход материалов на его изготовление. Однако объемная интенсивность может лишь до определенной степени служить мерой совершенства аппарата. Это объясняется тем, что объем­ная интенсивность аппарата связана с интенсивностью процесса, но с уве­личением коэффициента скорости процесса его интенсивность обычно воз­растает лишь до известного предела.

При оценке конструкции аппарата или режима его работы решающее значение должны иметь технико-экономические харак­теристики данного аппарата. Оптимальным будет такой аппарат (или такой режим его работы), который обеспечит заданный результат с наименьшими затратами.

Определение основных размеров аппаратов. Пользуясь уравнением (I,3), вычисляют основные размеры непрерывно действующего аппарата. Если известен объем Q среды, протекающей через аппарат в единицу вре­мени, и задана или принята ее линейная скорость w, то площадь по­перечного сечения S аппарата находят из следующего соотношения:

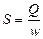(I,6)

По величине S определяют один из основных размеров аппарата, на­пример для аппарата цилиндрической формы — его диаметр D.

Другим основным размером является рабочая высота (или длина) Н аппарата. Из уравнения (I,3) находят рабочий объем аппарата (если А = V) или поверхность F, требуемую для проведения процесса. Зная F и пользуясь зависимостью F = aV, где а — поверхность, приходящаяся на единицу объема аппарата (удельная поверхность), рассчитывают его рабочий объем. По величине V определяют высоту Н, применяя соотно­шение V = SH. Рабочий объем V периодически действующего аппарата определяют как произведение заданной производительности (например, Q м⁸/сек) и периода процесса t сек, включающего продолжительность самого процесса, а также время, затрачиваемое на загрузку, выгрузку и другие вспомогательные операции:

V=Qt (I,7)

Моделирование и оптимизация процессов и аппаратов. Исследование процессов и аппаратов в масштабах и условиях промышленного производ­ства является, как правило, сложным, длительным и дорогостоящим. В связи с этим большое значение имеет моделирование — изуче­ние закономерностей процессов на моделях при условиях, допускающих распространение полученных результатов на все процессы, подобные изученному, независимо от масштаба аппарата.

Общие принципы моделирования вытекают из теории подобия. Согласно требованиям этой теории, должны соблюдаться следующие правила моделирования:

1) необходимо, чтобы процессы в модели и аппарате натурального раз­мера (оригинале) описывались одинаковыми дифференциальными уравнениями;

2) модель должна быть геометрически подобна оригиналу;

3) численные значения начальных и граничных условий, выражен­ных в безразмерной форме, для модели и оригинала должны быть равны;

4) необходимо, чтобы все безразмерные комплексы физических и гео­метрических величин, влияющих на процесс (критерии подобия), были равны во всех сходственных точках модели и оригинала.

Если последнее требование невыполнимо и протекание процесса прак­тически мало зависит от тех или иных критериев подобия, то равенством их в модели и оригинале пренебрегают, проводя приближенное моделирование.

Моделирование процессов можно также осуществлять на основе мате­матической аналогии — одинаковой формы уравнений, описывающих фи­зически различные явления. При использовании электронных вы­числительных машин математическое моделирование позволяет значи­тельно ускорить исследование наиболее сложных процессов химической технологии.

Заключительным этапом моделирования процессов является их оптимизация — выбор наилучших, или оптимальных, условий проведения процесса. Определение этих условий связано с выбором критерия оптимизации, который может зависеть от оптимальных значений ряда параметров (например, температуры, давления, степени извлече­ния и др.). Между указанными параметрами обычно существует сложная взаимосвязь, что сильно затрудняет выбор единого критерия, всесторонне характеризующего эффективность процесса. Задача сводится к поиску экстремального значения (минимума или максимума) целевой функции, выражающей зависимость величины выбранного критерия оптимизации от влияющих на него факторов.

Основные характеристики процесса, как правило, связаны между собой так, что возрастание его эффективности по одной из них снижает в той или иной степени эффективность данного процесса по другим харак­теристикам. Так, например, в любых процессах разделения смесей (ректи­фикация, экстракция, грохочение и др.) полное разделение недостижимо. Качество же конечного продукта, определяемое со­держанием в нем целевого компонента (или нескольких компонентов), улучшается с увеличением полноты разделения. Однако при этом процесс удорожается, а производительность аппара­туры уменьшается. В связи с этим задача оптимизации сводится, по су­ществу, к нахождению наиболее выгодного компромисса между значениями параметров, антагонистически влияющих на процесс.

Наиболее универсальны экономические критерии оптими­зации, интегрально отражающие (в стоимостном выражении) не только основные технические характеристики, подобные указанным выше, но и затраты на энергию, рабочую силу и т.д. Принцип нахождения экономического оптимума для отдельных основных процессов изло­жен в соответствующих главах курса. Однако необходимо отметить, что оптимизация на основе экономических критериев связана с наличием гибкой системы цен, оперативно отражающих изменение стоимости про­дуктов (в том числе промежуточных) с развитием науки и технического прогресса.

В зависимости от конкретных условий применяют также технологи­ческие, термодинамические, статистические и другие критерии оптими­зации.

Для оптимизации процессов широко используют кибернетические ме­тоды и при экспериментальном изучении — статистические методы пла­нирования экспериментов, позволяющие на основе предваритель­ного математического анализа сократить число опытов до минимально необходимого.

Основные математические методы оптимизации (классический матема­тический анализ, вариационное исчисление, линейное и динамическое программирование, принцип максимума и др.) описываются в специальной литературе.