Основные характеристики движения жидкостей
Скорость и расход жидкости. Рассмотрим движение жидкости по трубе постоянного сечения.
Количество жидкости, протекающей через поперечное сечение потока (его «живое» сечение, т.е. затопленное сечение трубопровода) в единицу времени, называют расходом жидкости. Различают объемный расход, измеряемый, например, в м3/сек или м3/ч, и массовый расход, измеряемый в кг/сек, кг/ч, и т.д.
В разных точках живого сечения потока скорость частиц жидкости неодинакова. Как будет показано, около оси трубы скорость максимальна, а по мере приближения к стенкам она уменьшается. Однако во многих случаях закон распределения скоростей в поперечном сечении потока неизвестен или его трудно учесть. Поэтому в расчетах обычно используют не истинные (локальные) скорости, а фиктивную среднюю скорость. Эта скорость w (м/сек) выражается отношением объемного расхода жидкости Q (м3/сек) к площади живого сечения S (м2) потока:
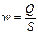
откуда объемный расход
Q = wS (II, 25)
Массовый расход М (кг/сек) определяется произведением
M =rwS (II,25а)
где r — плотность жидкости, кг/м3.
Величина rw представляет собой массовую скорость жидкости [в кг/(м3× сек)]:
W=rw (II,25б)
Выбор скоростей капельных жидкостей, газов и паров при расчетах трубопроводов рассмотрен позже.
Отметим, что приведенные основные характеристики движения жидкостей относятся к их перемещению в каналах с сечением любой формы.
Гидравлический радиус и эквивалентный диаметр. При движении жидкости через сечение любой формы, отличной от круглой, в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр.
Под гидравлическим радиусом rг (м) понимают отношение площади затопленного сечения трубопровода или канала, через которое протекает жидкость, т.е. живого сечения потока, к смоченному периметру:
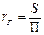 (II,26)
(II,26)
где S – площадь сечения потока жидкости, м2; П – смоченный периметр, м.
Для круглой трубы с внутренним диаметром d и, значит, площадью свободного сечения S = pd2/4 при сплошном заполнении его жидкостью П = pd, откуда гидравлический радиус
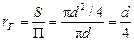
Диаметр, выраженный через гидравлический радиус, представляет собой эквивалентный диаметр:
d = dэ = 4rг (II,27)
Следовательно, согласно уравнению (II,26)
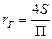 (II,27a)
(II,27a)
Эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади S к смоченному периметру П то же, что и для данного трубопровода некруглого сечения.
Для канала прямоугольного сечения со сторонами а и b, полностью заполненного жидкостью, гидравлический радиус
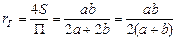
а эквивалентный диаметр
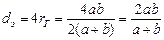
Для канала кольцевого поперечного сечения, в котором жидкость ограничена внутренней и наружной окружностями с диаметрами dВ и dH соответственно, эквивалентный диаметр
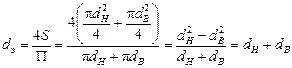
Для круглой трубы dэ = d.
Установившийся и неустановившийся потоки. Движение жидкости является установившимся, или стационарным, если скорости частиц потока, а также все другие влияющие на его движение факторы (плотности, температуры, давления и др.), не изменяются, во времени в каждой фиксированной точке пространства, через которую проходит жидкость. В этих условиях для каждого сечения потока расходы жидкости постоянны во времени.
При стационарном движении любой из указанных факторов, например скорость wx в некотором направлении х, может иметь различные значения в разных точках [wx = f (х, у, z)], но в любой точке скорость не изменяется со временем, т.е. 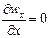 .
.
Пусть, например, установившееся движение жидкости происходит по трубе переменного сечения. Если за начало координат принять некоторую фиксированную точку на оси трубы, то скорость wx будет переменна в пространстве, увеличиваясь с уменьшением площади поперечного сечения трубы по оси х и уменьшаясь вдоль осей у и z по мере приближения к стенке трубы. Однако скорость wx будет постоянна во времени в любой точке.
В отличие от стационарного при неустановившемся, или нестационарном, потоке факторы, влияющие на движение жидкости, изменяются во времени. Так, скорость жидкости в определенном направлении х в любой точке является не только функцией пространственных координат х, у и z данной точки, но также времени t, т.е. wx = f (х, y, z, t). Значит, при этом 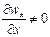 .
.
Примером неустановившегося движения может служить истечение жидкости из отверстия при переменном уровне ее в резервуаре: с понижением высоты столба жидкости в нем скорость истечения уменьшается во времени.
Установившиеся условия движения жидкости характерны для непрерывных процессов химической технологии. Неустановившееся движение жидкости происходит главным образом в периодических процессах или возникает кратковременно при пусках, остановках, а также изменениях режима работы аппаратов непрерывного действия.
Характеризуя различие между установившимся и неустановившимся движением жидкости частной производной по времени некоторого параметра потока (например, скорости 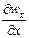 ), мы рассматривали изменение этого параметра в фиксированной точке пространства, имеющей постоянные координаты.
), мы рассматривали изменение этого параметра в фиксированной точке пространства, имеющей постоянные координаты.
Для каждой частицы движущейся жидкости изменение ее параметров во времени и в пространстве выражается не частной, а полной производной по времени, называемой в гидродинамике субстанциональной производной. По своему смыслу эта производная может быть названа также производной, следующей за потоком.
Обозначим через u любую величину, изменяющуюся в потоке, как во времени, так и в пространстве, например плотность, температуру, давление, концентрацию жидкости или любую из составляющих wx, wy и wz ее скорости w в направлениях осей координат.
Допустим, что мы наблюдаем за движением потока и можем мгновенно регистрировать значения и в каждый момент времени в данной точке потока. Если наблюдатель неподвижен, то изменение и за единицу времени в фиксированной точке пространства (х, у, z) = const выражается частной производной 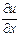 , а изменение и в указанной точке за бесконечно малый промежуток времени dt; составляет
, а изменение и в указанной точке за бесконечно малый промежуток времени dt; составляет 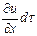 . Эта величина является местным, или локальным, изменением данной переменной, которое, как отмечалось, при установившемся движении равно нулю.
. Эта величина является местным, или локальным, изменением данной переменной, которое, как отмечалось, при установившемся движении равно нулю.
Если наблюдатель перемещается вместе с потоком (с какой-либо его частицей), то, измеряя значения и, можно установить, что изменение этой величины складывается из двух составляющих.
Пусть за время dt частица жидкости переместилась из точки А с координатами х, у и z в точку В с координатами (х + dx), (у + dy) и (z + dz).
В результате перемещения частицы в пространстве из точки А в точку В изменения и, соответствующие проекциям пути dx, dy и dz, равны 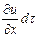 ,
, 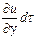 и
и 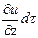 . Эти изменения не связаны с изменением и во времени в какой-либо фиксированной точке пространства. Таким образом, если бы движение частицы было установившимся (локального изменения и не было бы), то при переходе из A в В изменение и выражалось бы
. Эти изменения не связаны с изменением и во времени в какой-либо фиксированной точке пространства. Таким образом, если бы движение частицы было установившимся (локального изменения и не было бы), то при переходе из A в В изменение и выражалось бы
du = 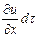 +
+ 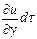 +
+ 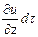
Это выражение характеризует конвективное изменение рассматриваемого параметра и.
Вследствие изменения и во времени в каждой точке пространства в условиях неустановившегося движения и = f (х, у, z, t), и за время dt значение указанного параметра также изменится на 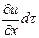 . Значит, полное изменение и при неустановившемся движении является суммой локального и конвективного изменений:
. Значит, полное изменение и при неустановившемся движении является суммой локального и конвективного изменений:
du = 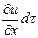 +
+ 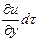 +
+ 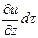 +
+ 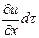
откуда
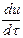 =
= 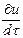 +
+ 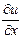 ×
× 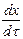 +
+ 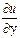 ×
× 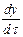 +
+ 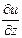 ×
× 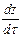
Однако
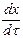 = wx,
= wx, 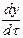 = wy и
= wy и 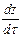 = wz,
= wz,
где wx, wy и wz — составляющие скорости вдоль соответствующих осей координат, на которые можно разложить скорость w.
Отсюда
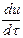 =
= 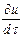 +
+ 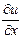 wx+
wx+ 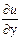 wy+
wy+ 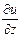 wz (II,28)
wz (II,28)
В частном случае установившегося процесса, когда 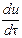 = 0
= 0
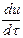 =
= 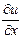 wx+
wx+ 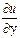 wy+
wy+ 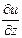 wz (II,28а)
wz (II,28а)
Уравнения (II,28) и (II,28a) выражают субстанциональную производную данного параметра. Использование специального термина для наименования полной производной сложной функции обусловлено тем, что составляющие скорости по осям координат ( 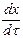 ,
, 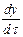 и
и 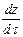 ) с которой перемещается наблюдатель, не произвольны, а принимаются равными составляющим скорости частицы жидкости (wx, wу и wz), так как наблюдатель перемещается вместе с потоком.
) с которой перемещается наблюдатель, не произвольны, а принимаются равными составляющим скорости частицы жидкости (wx, wу и wz), так как наблюдатель перемещается вместе с потоком.
Субстанциональная производная характеризует изменение какого-либо параметра или свойства материи (субстанции) во времени при перемещении материальных частиц в пространстве. В частности, при движении частицы жидкости со скоростью w конвективное и локальное изменения претерпевают все составляющие скорости вдоль осей координат (wx, wy и wz). Выражения субстанциональной производной применительно к отдельным составляющим скорости приведены ниже [см. уравнения (II,47)и (II,47а)]. В этом случае производные ( 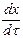 ,
, 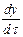 и
и 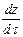 ) характеризуют составляющие ускорения вдоль соответствующих осей координат.
) характеризуют составляющие ускорения вдоль соответствующих осей координат.
Режимы движения жидкости. Различные режимы течения жидкости можно проследить, вводя в поток подкрашенную струйку жидкости или какой-либо иной индикатор.
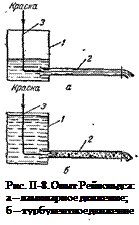
Впервые режимы течения жидкости изучались О. Рейнольдсом в 1883 г. на установке, изображенной на рис. II-8. К сосуду 1, в котором поддерживается постоянный уровень воды, присоединена горизонтальная стеклянная труба 2. В эту трубу по ее оси через капиллярную трубку 3 вводится тонкая струйка окрашенной воды (индикатор). При небольшой скорости воды в трубе 2 окрашенная струйка вытягивается в горизонтальную нить, которая, не размываясь, достигает конца трубы (рис. II-8, а). Это свидетельствует о том, что пути частиц прямолинейны и параллельны друг другу.
Такое движение, при котором все частицы жидкости движутся по параллельным траекториям, называют струйчатым, или ламинарным.
Если скорость воды в трубе 2 увеличивать сверх определенного предела, то окрашенная струйка сначала приобретает волнообразное движение, а затем начинает размываться, смешиваясь с основной массой воды. Это объясняется тем, что отдельные частицы жидкости движутся уже не параллельно друг другу и оси трубы, а перемешиваются в поперечном направлении (рис. II-8, б).
Такое неупорядоченное движение, при котором отдельные частицы жидкости движутся по запутанным, хаотическим траекториям, в то время как вся масса жидкости в целом перемещается в одном направлении, называют турбулентным.
 В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости, движущиеся в главном (осевом) направлении, получают также поперечные перемещения, приводящие к интенсивному перемешиванию потока по сечению и требующие соответственно большей затраты энергии на движение жидкости, чем при ламинарном потоке.
В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости, движущиеся в главном (осевом) направлении, получают также поперечные перемещения, приводящие к интенсивному перемешиванию потока по сечению и требующие соответственно большей затраты энергии на движение жидкости, чем при ламинарном потоке.
Опыт показывает, что переход от ламинарного течения к турбулентному происходит тем легче, чем больше массовая скорость жидкости rw и диаметр трубы d и чем меньше вязкость жидкости m. Рейнольдс установил, что указанные величины можно объединить в безразмерный комплекс wdr/m, значение которого позволяет судить о режиме движения жидкости. Этот комплекс носит название критерия Рейнольдса (Re):
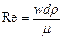 (II,29)
(II,29)
Критерий Re является мерой соотношения между силами вязкости и инерции в движущемся потоке. В самом деле, вероятность нарушения ламинарного режима течения и возникновения хаотического перемещения частиц тем больше, чем меньше вязкость жидкости, препятствующая этому нарушению, и чем больше ее плотность, представляющая собой меру инерции отклонившихся от прямолинейного движения частиц. Поэтому при равных скоростях движения различных жидкостей в трубах одинакового диаметра турбулентность возникнет тем легче, чем больше r и меньше m, или чем меньше кинематическая вязкость n = m/r. Соответственно критерий Рейнольдса может быть записан в виде
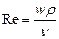 (II,29а)
(II,29а)
Переход от ламинарного к турбулентному движению характеризуется критическим значением Reкp. Так, при движении жидкостей по прямым гладким трубам Reкp » 2320. При Re < 2320 течение обычно является ламинарным, поэтому данную область значений Re называют областью устойчивого ламинарного режима течения. При Re > 2320 чаще всего наблюдается турбулентный характер движения. Однако при 2320 < Re < 10000 режим течения еще неустойчиво турбулентный (эту область изменения значений Re часто называют переходной). Хотя турбулентное движение при таких условиях более вероятно, но иногда при этих значениях Re может наблюдаться и ламинарный поток. Лишь при Re > 10 000 турбулентное движение становится устойчивым (развитым).
Указанное значение Reкр = 2320 является условным, так как оно относится лишь к стабилизированному изотермическому потоку в прямых трубах с очень малой шероховатостью стенок. Наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением значения скорости потока или ее направления, близостью входа в трубу и т.п., может существенно снижать величину Reкp. Критическое значение Re уменьшается и при неизотермичности потока по сечению трубы из-за возникновения конвективных токов жидкости в направлении, перпендикулярном к оси трубы.
Для газов плотность примерно на три, а вязкость на 1.5-2 порядка ниже, чем для капельных жидкостей. Поэтому Reкp и турбулентный режим движения для газов достигаются при значительно больших скоростях, чем для капельных жидкостей (при равных d).
В случае движения жидкости через каналы некруглого сечения при расчете критерия Re вместо d используют эквивалентный диаметр, определяемый отношением (II,27а).
В выражение для критерия Рейнольдса входит средняя скорость потока, характеризуемая уравнением (II,25). Действительные же скорости жидкости неодинаковы в разных точках сечения трубопровода. При этом распределение указанных скоростей по сечению потока различно для ламинарного и турбулентного движения. Для ламинарного потока вид распределения скоростей может быть установлен теоретически.
Распределение скоростей и расход жидкости при установившемся ламинарном потоке. В случае ламинарного движения вязкой жидкости в прямой трубе круглого сечения всю жидкость можно мысленно разбить на ряд кольцевых слоев, соосных с трубой (рис. II-9, а).
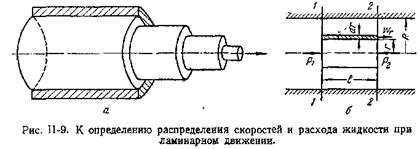
Вследствие действия между слоями сил трения слои будут двигаться с неодинаковыми скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную скорость, но, по мере удаления от оси, скорость элементарных кольцевых слоев будет уменьшаться. Непосредственно у стенки жидкость как бы «прилипает» к стенке, и ее скорость здесь обращается в нуль.
Выделим в потоке жидкости, ламинарно движущемся по трубе радиусом R (рис. II-9, б), цилиндрический слой длиной l и радиусом r.
Движение слоя происходит под действием разности сил давления P1 и P2 с обеих торцовых сторон цилиндра:
Р1-Р2=(р1-p2)pr2
где p1, р2 — гидростатические давления в сечениях l—l и 2—2.
Движению цилиндра оказывает сопротивление сила внутреннего трения T, для которой, согласно уравнению (II,11) с учетом (II,12а), справедливо выражение
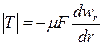
где wr — скорость движения жидкости вдоль оси цилиндра на расстоянии r от оси; F = 2prl — наружная поверхность цилиндра; m — вязкость жидкости.
Знак минус указывает на убывание скорости с увеличением радиуса r (приr r — R величина wr = 0).
При установившемся движении разность сил давления Pt—P2 затрачивается на преодоление силы трения Т, и сумма проекций всех этих сил на ось потока должна быть равна нулю. Вследствие трения движение рассматриваемого цилиндрического слоя тормозится, значит, сила трения, приложенная к его боковой поверхности, направлена противоположно разности Р1 — Р2 и проектируется на ось, направление которой совпадает с направлением движения, со знаком минус. Следовательно
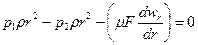
или
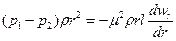
откуда, после сокращения и разделения переменных, получим
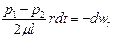
Переходя ко всему объему жидкости в трубе, проинтегрируем это дифференциальное уравнение, учитывая, что радиус в левой части уравнения изменяется от r до r = R, а переменная скорость в правой части — от w = w1 до w = 0 (у стенки, где r = R):
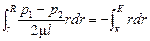
Тогда
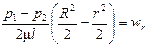
или
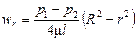 (II,30)
(II,30)
Скорость имеет максимальное значение на оси трубы, где r = 0:
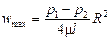
Сопоставляя выражения (II,30) и (II,30а), находим
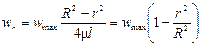 (II,31)
(II,31)
Уравнение (II,31) представляет собой закон Стокса, выражающий параболическое распределение скоростей в сечении трубопровода при ламинарном движении.
Для определения расхода жидкости при ламинарном движении рассмотрим элементарное кольцевое сечение (рис. II-9, б) с внутренним радиусом r и внешним радиусом (r + dr), площадь которого равна dS = 2prdr. Объемный расход жидкости через это сечение составляет
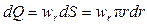
или с учетом уравнения (11,30)
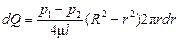
Интегрируя последнее уравнение, получим общий расход жидкости через трубу:
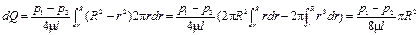 (II,32)
(II,32)
Подставляя вместо R диаметр трубы d = 2R и обозначая (р1 - р2) = Dp, окончательно находим
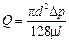 (II,32a)
(II,32a)
Уравнение (II,32) или (II,32а), определяющее расход жидкости при ее ламинарном движении по круглой прямой трубе, носит название уравнения Пуазейля.
Соотношение между средней скоростью w и максимальной скоростью wmax можно получить, сопоставив значение Q из уравнений (II,25) и (II,32):
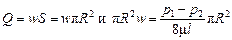
откуда
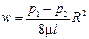 (II,34)
(II,34)
Сравнивая уравнения (II,30а) и (II,33), находим
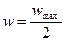 (II,34)
(II,34)
Таким образом, при ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы,
Соответственно параболический закон распределения скоростей по сечению трубы, выражаемый уравнением (II,31), может быть представлен в виде
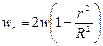 (II,31a)
(II,31a)
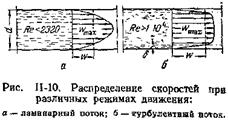
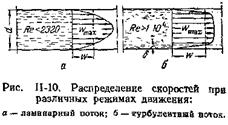
Этот закон, выведенный теоретически, хорошо подтверждается эпюрами скоростей, полученными опытным путем (рис. II-10, a).
Некоторые характеристики турбулентного потока. В промышленной практике наиболее распространено турбулентное движение жидкостей.
При турбулентном движении из-за хаотического движения частиц происходит выравнивание скоростей в основной массе потока и их распределение по сечению трубы характеризуется кривой, отличающейся по форме от параболы на рис. II-10, а; кривая имеет значительно более широкую вершину (рис. II-10, б).
Опыт показывает, что средняя скорость w при турбулентном движении не равна половине максимальной (как для ламинарного движения), а значительно больше, причем w/wmax = f(Re). Например, при Re = 104 скорость w » 0.8wmax, а при Re = 108 величина w » 0.8wmax.
В связи со сложным характером турбулентного движения не представляется возможным строго теоретически получить профиль распределения скоростей и значение w/wmax. Кроме того, при турбулентном потоке профиль скоростей (рис. II-10, б) выражает распределение не истинных, а осредненных во времени скоростей.
 В каждой точке турбулентного потока истинная скорость не остается постоянной во времени из-за хаотичности движения частиц. Ее мгновенные значения испытывают флуктуации, или нерегулярные пульсации, носящие хаотический характер.
В каждой точке турбулентного потока истинная скорость не остается постоянной во времени из-за хаотичности движения частиц. Ее мгновенные значения испытывают флуктуации, или нерегулярные пульсации, носящие хаотический характер.
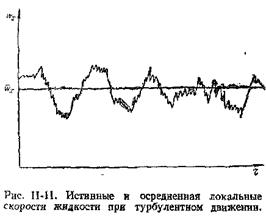
Типичная картина изменения составляющей истинной мгновенной скорости wx, (вдоль оси х потока) для некоторой точки в зависимости от времени t представлена на рис. II-11. Саму истинную скорость измерить практически невозможно из-за хаотического перемещения частиц во всех направлениях. Как видно из рисунка, скорости пульсируют около некоторого осредненного во времени значения, становясь то больше, то меньше его. Для данной точки осредненная во времени скорость wx может быть найдена из соотношения
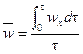 (II,35)
(II,35)
Таким образом, величина wx равна высоте прямоугольника, равновеликого площади, заключенной между пульсационной кривой и осью абсцисс в пределах изменения времени от 0 до t (см. рис. II-11).
Разность между истинной и осредненной скоростями называют мгновенной пульсационной скоростью и обозначают через Dw (индекс х здесь и далее опускаем):
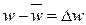 (II,36)
(II,36)
Согласно рис. II-11, величина Dw имеет переменный знак, поэтому
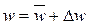 (II,36a)
(II,36a)
Понятие осредненной скорости не следует путать с введенным ранее понятием средней скорости w. Последняя представляет собой не среднюю во времени скорость в данной точке, а скорость, осредненную для всего поперечного сечения трубопровода.
Несмотря на кажущуюся беспорядочность изменения скоростей при турбулентном движении, значение осредненной скорости за достаточно большой промежуток времени t остается постоянным. При этом достаточно большим может считаться уже период времени, измеряемый секундами или даже, долями секунды, так как частота пульсаций скорости очень велика. Поэтому вместо изменения мгновенных скоростей можно рассматривать независимое от времени изменение осредненных скоростей по сечению трубопровода (рис. II-10, б), хотя турбулентное движение по существу не является установившимся. Таким образом, осреднение скоростей во времени позволяет приближенно считать это движение стационарным. В этом смысле турбулентное движение может рассматриваться как квазистационарное.
Интенсивность турбулентности выражается отношением
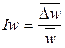 (II,37)
(II,37)
где 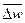 — среднее квадратичное значение пульсационной скорости, с помощью которого осредняются во всех направлениях мгновенные пульсационные скорости по их абсолютной величине.
— среднее квадратичное значение пульсационной скорости, с помощью которого осредняются во всех направлениях мгновенные пульсационные скорости по их абсолютной величине.
Интенсивность турбулентности является мерой пульсаций в данной точке потока. При турбулентном течении по трубам It » 0.01-0.1.
Если средние пульсации скорости одинаковы по всем направлениям, то такая турбулентность называется изотропной.
Турбулентность практически всегда в той или иной степени отличается от изотропной, приближаясь к ней вблизи оси развитого турбулентного потока и все больше отклоняясь от нее в поперечном направлении, по мере приближения к стенке трубы.
Помимо интенсивности It другими важными характеристиками турбулентного движения являются масштаб турбулентности и турбулентная вязкость.
Чем ближе друг к другу находятся две частицы жидкости в турбулентном потоке, тем более близки их истинные (мгновенные) скорости. В тоже время у достаточно удаленных одна от другой частиц совсем нет связи между колебаниями, или пульсациями, их скоростей. Достаточно близко расположенные частицы, движущиеся совместно, можно считать принадлежащими к некоторой единой совокупности, называемой обычно вихрем. Размер таких вихрей, или глубина их проникания до разрушения, которая приближенно может быть отождествлена с расстоянием между двумя ближайшими частицами, уже не принадлежащими к одному вихрю, зависит от степени развития турбулентности в потоке, или ее масштаба, и поэтому носит название масштаба турбулентности.
В указанном выше смысле термин «вихрь» — условное понятие. Вихревым является и ламинарное движение, которое характеризуется различием скоростей по сечению трубы (см. рис. II-10, а). Каждая частица жидкости движется по трубопроводу поступательно, однако поток в любом сечении можно считать как бы вращающимся вокруг его точек, находящихся у стенки, где скорость жидкости равна нулю. Таким образом, отличие ламинарного течения от турбулентного состоит не в том, что последнее является вихревым, а в наличии хаотических флуктуаций скорости в различных точках турбулентного потока, приводящих, в частности, к перемещению частиц в направлениях, поперечных его оси.
Для характеристики турбулентной вязкости рассмотрим две частицы жидкости в турбулентном потоке, движущемся в направлении оси х, параллельно оси трубы. Пусть расстояние между частицами в направлении, перпендикулярном оси трубы, равно dy. Составляющие скорости частиц по направлению потока wх1 и wх2 отличаются друг от друга на dwx, причем вследствие разности скоростей возникает касательное напряжение tн определяемое по уравнению (II,12а):
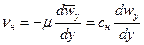 (II,38)
(II,38)
где m и n — динамическая и кинематическая вязкости; r — плотность жидкости; индекс "н" при n означает "ньютоновское".
В ламинарном потоке tн было бы единственным напряжением, возникающим между расположенными на расстоянии dy слоями жидкости. Однако в турбулентном потоке частицы жидкости перемещаются относительно друг друга не только в продольном (вместе с потоком), но и в поперечном направлении. Это создает дополнительное касательное напряжение nт (индекс «т» — турбулентное), которое по аналогии с nн можно выразить уравнением
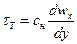 (II,39)
(II,39)
Величину tт называют коэффициентом турбулентной вязкости, или просто турбулентной вязкостью.
Турбулентная вязкость, в отличие от обычной вязкости, не является физико-химической константой, определяемой природой жидкости, ее температурой и давлением. Турбулентная вязкость зависит от скорости жидкости и других параметров, обусловливающих степень турбулентности потока (в частности, расстояния от стенки трубы и т.д.).
Суммарное касательное напряжение в потоке определяется, следовательно, как вязкостью жидкости, так и турбулентностью потока:
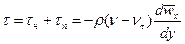 (II,40)
(II,40)
Из рис. II-10,б видно, что в основной массе потока скорости жидкости в значительной мере выравнены по сечению трубы. Однако вблизи стенки трубы скорость резко снижается, обращаясь у самой стенки в нуль. В непосредственной близости от стенки, с приближением к ней, движение жидкости становится все менее турбулентным и все более ламинарным, вследствие того, что твердая стенка как бы "гасит" турбулентные пульсации в поперечном направлении.
Условно различают центральную зону, или основную массу жидкости, называемую ядром потока, в которой движение является развитым турбулентным, и гидродинамический пограничный слой вблизи стенки, где происходит переход турбулентного движения в ламинарное.
Внутри этого слоя имеется тонкий подслой (у стенки трубы) толщиной d, где силы вязкости оказывают превалирующее влияние на движение жидкости. Поэтому характер ее течения в подслое в основном ламинарный. Градиент скорости в ламинарном пограничном подслое очень высок, причем у самой стенки скорость равна нулю.
Ламинарный подслой в турбулентном потоке характеризуется очень малой толщиной (составляющей иногда доли миллиметра), которая уменьшается с возрастанием турбулентности потока. Однако явления, происходящие в нем, как будет видно из дальнейшего, оказывают значительное влияние на гидравлическое сопротивление при движении жидкости, а также на протекание процессов тепло- и массообмена.
Между ядром потока и ламинарным подслоем существует переходная зона, причем ламинарный подслой и эту зону иногда называют гидродинамическим пограничным слоем. Толщина его определяется тем, что напряжения сдвига между частицами жидкости в пограничном слое, обусловленные ее вязкостью и турбулентными пульсациями, а, следовательно, значения n и nt [см. уравнение (II,40)] становятся сравнимыми по порядку.
Из приведенного упрощенного представления о структуре турбулентного потока следует, что турбулентное движение всегда сопровождается ламинарным у твердой границы потока (у стенки трубы). В действительности структура турбулентного потока является более сложной, так как четких границ между названными зонами не существует. Поэтому точнее использовать представление не о чисто ламинарном, а о вязком подслое, в котором влияние вязкости преобладает над влиянием турбулентных пульсаций, т.е. его толщина характеризуется тем, что в этом подслое n > nt.
Дата добавления: 2016-02-16; просмотров: 5203;
