Спектральный анализ (CA) в MatLab

Основная задача СА сигналов - выявление гармонического спектра этих сигналов, т.е. определение частот гармонических составляющих сигнала (выявление частотного спектра), амплитуд этих гармонических составляющих (амплитудного спектра) и их начальных фаз (фазового спектра).

Любой периодический процесс может быть представлен в виде так называемого комплексного ряда Фурье:

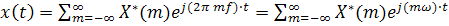(4.1)

где 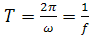, где ω - циклическая (круговая) частота периодического процесса.

Комплексные амплитуды X* (т):

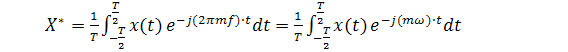(4.2)

Таким образом, частотный спектр периодических колебаний состоит из частот, кратных основной (базовой) частоте f, т.е. частот fm = m-f, m = 0, 1,2...

Действительные и мнимые части комплексной амплитуды X (т), образуют соответственно действительный и мнимый спектры периодических колебаний. Если комплексные амплитуды представить в

экспоненциальной форме: Х*(т) = 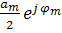, где а_т - амплитуда

гармонической составляющей f_m , φ_т - начальная фаза этой гармоники, имеющей форму косинусоиды, то исходный процесс можно записать в виде

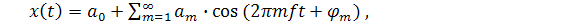(4.3)

который собственно и называется рядом Фурье.

Для действительных процессов справедливо:

R_e{Х(-т)} = R_e {Х{т)}; φ_т {Х(-т)} = -φ_т {Х(т)}

Разложения (4.1) и (4.3) позволяют рассматривать совокупность комплексных амплитуд (4.2) как изображение периодического процесса в частотной области. Для непериодического процесса тоже вводится понятие Фурье-изображения:

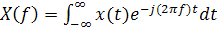(4.4)

Интеграл (4.4) существенно отличается от (4.2), несмотря на их внешнее сходство: 1) физическая размерность комплексной амплитуды совпадает с размерностью самой величины x(t), а размерность Фурье-изображения равна размерности x(t), умноженной на размерность времени; 2) интеграл (4.4) существует (сходится к конечной величине) только для «двусторонне затухающих» процессов, т.е. →0 при t→±∞.

Иначе говоря, его нельзя применять к так называемым «стационарным» колебаниям.

Обратное преобразование Фурье - изображение в исходный процесс x(t) в этом случае определяется интегралом:

(4.5)

т.е. представляет собой некий аналог комплексного ряда Фурье (4.1).

Указанное серьезное противоречие несколько сглаживается при численных расчетах, т.к. в этом случае можно иметь дело только с процессами ограниченной длительности, причем сам процесс в заданном диапазоне времени должен быть задан своими значениями в ограниченном числе точек.

Интегрирование заменяется суммированием:

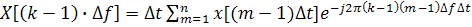(4.6)

Непрерывное время t → (т - 1)∆t, где т - номер точки от начала процесса.

Непрерывные значения частоты f→(k— 1)∆t, где k - номер значения

частоты, дискрет частоты ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 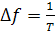, где T - промежуток времени, на котором

задан процесс.

Дифференциал dt → ∆t.

Если обозначить ∆t, как Ts, ввести обозначения:

х(т) = х[(т -1)∆t; X(k)X[(k-1)∆f], и учесть, что число точек, в которых задан процесс, равно:

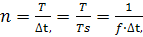, то (4.5) приводится к виду:

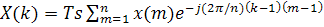(4.7)

В Matlab есть процедуры fft и ifff.

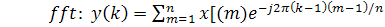(4.8)

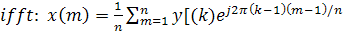(4.9)

Таким образом, fft находит дискретное Фурье-изображение заданного дискретного во времени процесса x(t), поделенное на дискрет времени Ts:

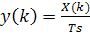(4.10)

Для комплексной амплитуды Х^* (k) получим

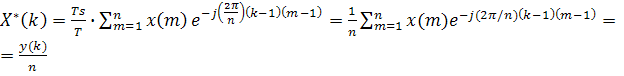(4.11),

откуда следует, что комплексный спектр разложения стационарного процесса равен поделенному на число измерений результату применения процедуры fft к заданному вектору измеренного процесса.

Если принять во внимание, что для стационарных колебательных процессов именно частотный, амплитудный и фазовый спектры не зависят от длительности Т конкретной реализации и выбранного дискрета времени Ts, то надо также. сделать вывод, что для спектрального анализа стационарных процессов наиболее целесообразно применять процедуру//?, результат которой делить затем на число точек измерений.

Фурье-изображение полигармонического процесса

Рассмотрим пример трехчастотных гармонических колебаний - с частотой 1/π, 1 и 3 Гц и амплитудами соответственно 0.6, 0.3 и 0.7:

y(t) = 0.6 cos(2t) + 0.3 sin(2πt) + 0.7 cos(6πt + π/4)

Построим графики процесса y(t), модуля его Фурье-изображения, действительную и мнимую его части.

1. По заданному значению дискрета времени Ts рассчитать F_max диапазона частот (в Гц) по формуле

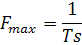
2. По заданной длительности процесса Г рассчитать дискрет частоты df по формуле

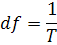
3. По вычисленным данным сформировать вектор значений частот, в которых будет вычислено Фурье-изображение. Это делается (но не наиболее правильно) так:

В результате применения процедуры fft будет получено представление процесса в частотной области. Обратная процедура iff, если ее применить к результату первого преобразования, дает возможность восстановить исходный процесс во временной области. Однако процедура fft не дает непосредственно Фурье-изображение процесса. Чтобы получить Фурье-изображение, необходимо выполнить следующие преобразования:

1. К результатам действия процедуры fft применить процедуру fft shift, которая меняет местами первую и вторую половину полученного вектора.

2. Перестроить вектор частот по алгоритму:

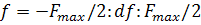
График процесса:

Ts=0.01; Т=100;

t=0:Ts:T;

proz=0.6*cos(2*t)+0.3*sin(2*pi*t)+0.7*cos(6*pi*t+pi/4)

plot (t,proz), grid, Set (gca, FontName', 'ArialCyr', FontSize', 16),

title (" Трехчастотный полигармонический процесс ');

xlabel ('Время (с)');

ylabel ('у (t)')

Модуль Ф-изображения этого процесса:

df=l/T; F_max=l/Ts; dovg=length (t);

f=- F_max /2: df: F_max /2;

X=fft(y);Xp=fft shift (X);

A=abs (Xp);

S1=dovg/2-400; S2=dovg/2+400;

Stem (f(S1:S2), A (S1:S2)), grid,

Set (gca, 'FontName', 'ArialCyr', 'FontSize', 14),

Title ('Модуль Фурье изображения полигармонического процесса '):

xlabel ('Частота (Гц) ');

ylabel ('Модуль')

(Изменить дискрет времени на Ts = 0.02).

Видно, что результат Фурье(Ф)-преобразования в значительной степени зависит от величины дискрета времени и мало что говорит об амплитудах гармонических составляющих. Это обусловлено различием между определением Ф-изображения и комплексного спектра. Поэтому для незатухающих (т.е. установившихся, стационарных) колебаний любого вида намного удобнее находить не Ф-изображение, а величину, деленную на число точек в реализации. В предыдущей части программы это эквивалентно замене X=fft (у) на X=fft (y)/dovg, где dovg - длина вектора t.

В результате получится комплексный спектр, полностью соответствующий коэффициентам комплексного ряда Фурье.

Выделяем действительную и мнимую части комплексного спектра:

dch=real (Xp); mch=imag (Xp);

Sl=dovg/2-400; S2=dovg/2+400;

Subplot (2, 1, 1)

Plot (f(S1:S2), dch (S1.S2)), grid,

Set (gca, FontName', 'ArialCyr', FontSize', 10),

title ("Комплексный спектр полигармонических колебаний');

ylabel ("Действительная часть')

Subplot (2, 1, 2)

Plot (f(S1:S2), mch (S1.S2)), grid,

Set (gca, 'FontName', 'ArialCyr', 'FontSize', 10),

xlavel ("Частота (Гц)',);

ylabel ("Мнимая часть',)