Обработанная информация

Физическая величина, являющаяся полезной (несущей в себе информацию), редко имеет такую физическую форму, что может быть непосредственно измеренной. Обычно она представляет лишь некоторую составляющую некоторой другой физической величины, которая может быть непосредственно измерена. Связь между этими двумя величинами обозначим введением звена, которое назовём первичным преобразователем (ПП). Обычно закон преобразователя известен заранее, иначе восстановить информационную составляющую в дальнейшем было бы невозможно. ПП вносит зависимость сигнала, который может быть измерен, от некоторых других физических величин. Поэтому выходная его величина содержит кроме полезной информационной составляющей, другие компоненты, искажающие полезную информацию. Назовём вносимую вредную составляющую ПП шумом ПП. Далее образованная таким образом непосредственно измеряемая величина измеряется измерителем, который так же вносит искажения - шумы измерителя.

Не ограничивая общности, будем считать выходную величину электрическим сигналом, который довольно просто преобразовать электрическими устройствами.

Для осуществления цифровой обработки измеренная величина должна быть преобразована в дискретную форму при помощи специального устройства, которое содержит экстраполятор и АЦП. Первый производит фиксацию отдельного текущего значения измеренной величины в отдельные моменты времени через постоянный промежуток времени, называемый дискретом времени. Второй (АЦП) - переводит его значение в цифровую форму (здесь тоже есть шумы, но они значительно меньше шумов ПП и измерителя).

Для того, чтобы на основе имеющегося дискретизированного сигнала получить полезный сигнал, нужно создать устройство или программу для ЭВМ, которая осуществила бы такие преобразования входного дискретного во времени сигнала, чтобы на его выходе искажения, внесённые шумами ПП и измерителя, были минимизированы в некотором смысле. Это устройство называют фильтром.

В общем случае создание (проектирование фильтра) является задачей неопределённой, которая конкретизируется на основе информации о модели ПП, модели измерителя, о характеристиках изменения во времени шумов, о закономерностях их влияния на искажение полезной информации.

Традиционно задачу фильтрации решают только для некоторых наиболее распространённых на практике, чаще всего линейных моделей ПП и измерителя.

В общем случае процесс создания фильтра включает следующие этапы:

1. На основе априорной информации о моделях ПП и измерителя и о характеристиках шумов, а также о задачах, которые должен решать фильтр, выбирается некоторый тип фильтра из известных, с разработанной теорией проектирования.

2. На основе конкретных числовых данных рассчитываются числовые характеристики выбранного типа фильтра (создаётся конкретный фильтр).

3. Проверяется эффективность выполнения разработанным фильтром поставленной задачи:

а) смоделировать на ЭВМ дискретный сигнал, содержащий полезную (информационную) составляющую с наложенными на неё предусмотренными шумами ПП и измерителя;

б) пропустить его через построенный фильтр и сравнить полученный на выходе сигнал с известной (в данном случае) полезной его составляющей - разность между ними будет характеризовать погрешности измерения на выходе фильтра.

4. Так как в реальных условиях некоторые характеристики шумов могут отличаться от принятых при проектировании (создании фильтра), могут быть полезны испытания эффективности работы фильтра в условиях, более приближённых к реальным, нежели принятые при проектировании.

Пакет SPT (Signal Processing Toolbox) позволяет осуществить операции 2, 3,4, а также:

1. Проектировать (рассчитывать конкретные числовые характеристики) цифровые и аналоговые фильтры по требуемым амплитудно- и фазо-частотным их характеристикам.

2. Формировать последовательности типовых временных сигналов и обрабатывать их спроектированными фильтрами.

3. Осуществлять преобразование Фурье, Гильберта, статистический анализ.

4. Рассчитывать корреляционные функции, спектральную плотность мощности сигнала, оценивать параметры фильтров по измеренным обсчетам входной и выходной последовательностей.

Сокращения, принятые в цифровой обработке сигналов:

АУХ - амплитудно-частотная характеристика.

БИХ - фильтр с импульсной характеристикой бесконечной длины.

БПФ - быстрое преобразование Фурье.

ГВЗ - групповое время замедления.

ДКП - дискретное косинусное преобразование.

ДПФ - дискретное преобразование Фурье.

КИХ - фильтр с импульсной характеристикой конечной длины.

СКО - средняя квадратическая ошибка.

СПМ - спектральная плотность мощности.

ФВЧ (ВЧ) - фильтр верхних частот.

ФНЧ (НЧ) - фильтр нижних частот.

ФЧХ- фазочастотная характеристика.

ФМ - фазовая модуляция.

ЧМ - частотная модуляция.

ФИМ- фазоимпульсная модуляция.

Х(1) - первый элемент последовательности X, соответственной нулевой временной задержке.

f - частота, Гц (при описании дискретной системы)

ω или W - угловая частота, рад; при использовании нормализованной частоты значение 1 соответствует частоте Найквиста, которая равна половине частоты дискретизации.

Ω — угловая частота, рад. (используется для описания непрерывных систем).

Моделирование типовых сигналов

1. у = rectpuls(t)

2. у = rectpuls(t,W)

Прямоугольный импульс

1. Формирует прямоугольный импульс одиночной амплитуды для заданной в векторе t последовательности отчетов времени. Генерируется импульс с шириной 1, центрированный относительно t = 0. В векторе у формируется часть импульса, соответствующие последовательности отсчетов, заданной в векторе t (по умолчанию здесь W=l).

2. Формирует импульс ширины W.

>>t = 0: 0.01: 10;

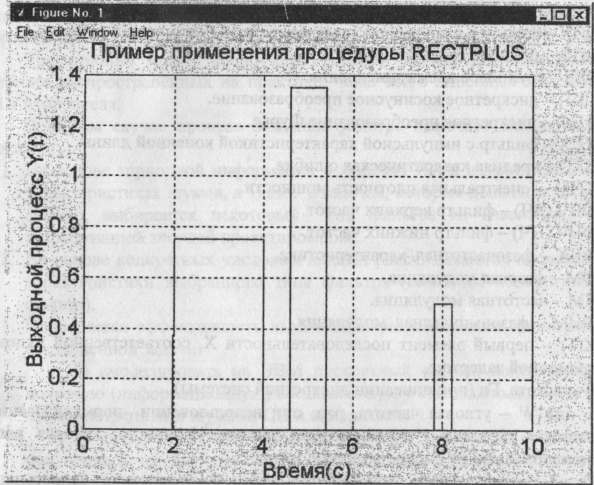
>>у = 0.75*rectpuls (t-3,2)+0.5*rectpuls (t-8, 0.4)...

+1.35*rectpuls(t-5, 0.8)

>>plot (t, y), grid, set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)

>>title ('Пример применения процедуры RECTPULS')

>>xlabel ('Время (с)')

>>ylabel ('Выходной процесс Y (t)')

1. у = tripuls (t)

2. у = tripuls (t, W)

3. у = tripuls (t, W, s)

Треугольный импульс

1., 2., - то же, что и прямоугольный

3. Формирует треугольный импульс, наклон которого определяется параметром S, где -1<S<1. Для симметричного импульса S=0

(или не указан 2)

>>t = 0: 0.01: 10;

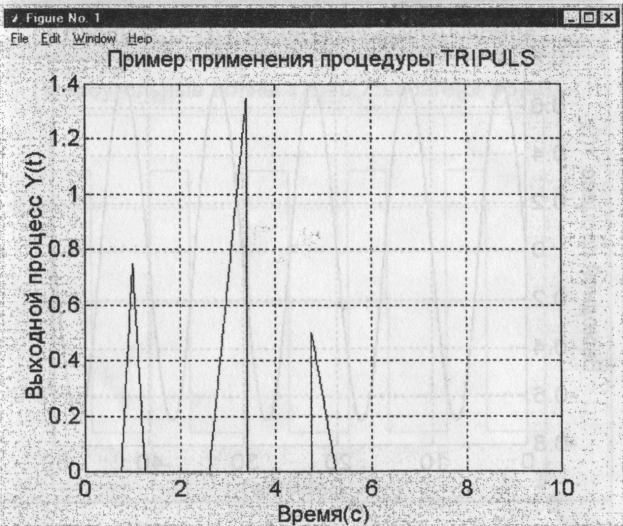
>>у = 0.75*tripuls (t-l,0.5)+0.5*tripuls (t-5, 0.5, -1)...

+1.35*tripuls(t-3, 0.8, 1);

>>plot (t, y), grid, set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)

>>title ('Пример применения процедуры TRIPULS')

>>xlabel ('Время (с)')

>>ylabel ('Выходной процесс Y (t)')

sin (x)

cos (x)

Полигармонические колебания

>>t = 0:0.01: 50;

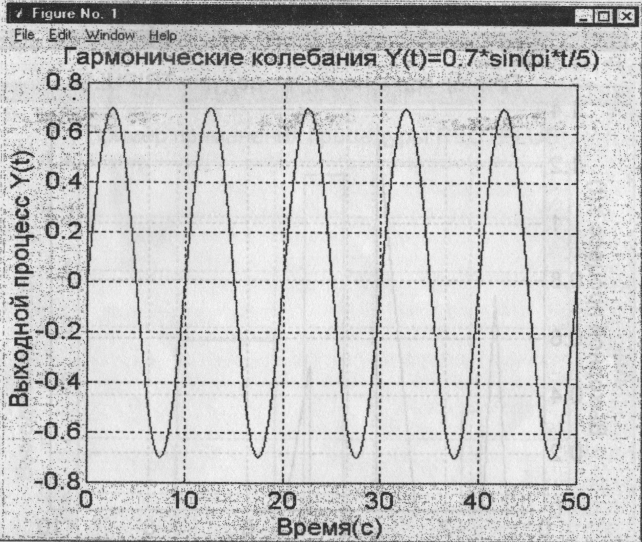
>>y1 = 0.7*sin (pi * t/5)

>>plot (t, y1), grid, set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)

>>title ('Гармонические колебания Y (t)=0.7*Sin (pi *t/5)')

>>xlabel ('Время (с)')

>>ylabel ('Выходной процесс Y (t)')

y=Square (t)

y=Square (t, duty)

Последовательность прямоугольных импульсов

Амплитуда = ±1.

duty - продолжительность положительной полуволны, которая определяется параметрами duty, в процентах от периода.

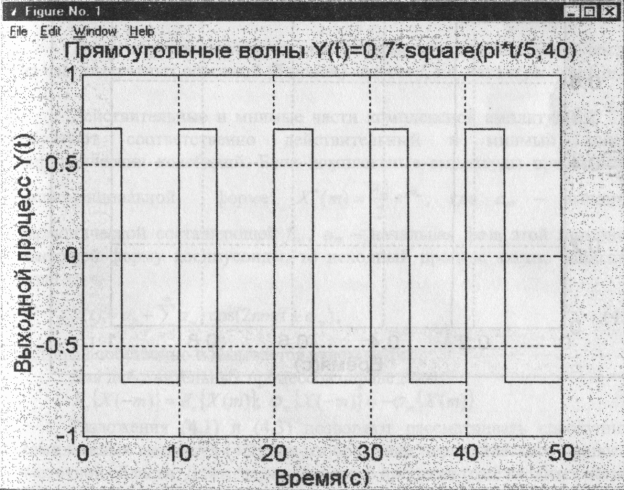
>>t=0: 0.01: 50; » y=0.7*Square (pi*t/5, 40);

>>plot (t, у), grid, set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)

>>title ('Прямоугольные волны' Y (t)=0.7*Square (pi *t/5, 40)')

>>xlabel ('Время (с)')

>>ylabel ('Выходной процесс Y (t)')

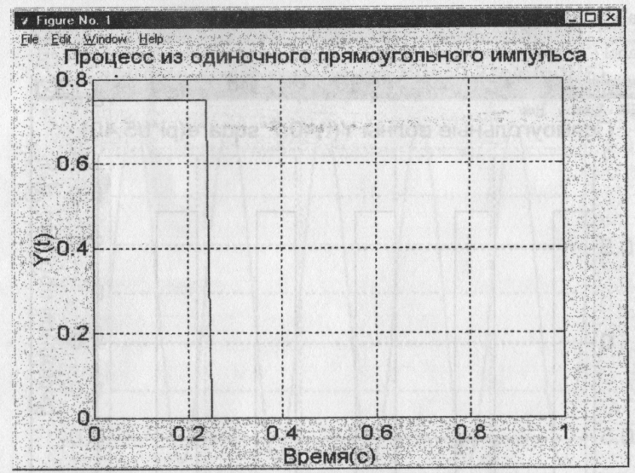
Ts=0.01; T=100; A=0.75; w=0.5;

t=0: Ts: T;

y=A* rectpuls(t, w);

plot(t(l:100), y(l:100)), grid, set(gca, 'FontName',...

'ArialCyr', 'FontSize', 16);

title('Процесс из одиночного прямоугольного импульса');

хlаbеl('Время(с)');

ylabel ('Y(t)');