Общие средства фильтрации
Рассмотрим основы линейной фильтрации на примере линейного стационарного фильтра, который в непрерывном времени описывается дифференциальным уравнением 2-го порядка:
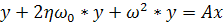 (4.12)
(4.12)
где х - заданный процесс, подаваемый на вход фильтра (4.12) 2-го порядка.
у - процесс, получаемый на выходе фильтра.
 - частота собственных колебаний фильтра.
- частота собственных колебаний фильтра.
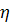 - относительный коэффициент затухания этого фильтра.
- относительный коэффициент затухания этого фильтра.
Передаточная функция этого фильтра имеет вид:
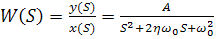 (4.13)
(4.13)
Для контроля и графического представления передаточной функции любого динамического звена удобно использовать процедуру freqs.
Общий вид обращения к ней: h=freqs (b, a, W)
Процедура создает вектор h комплексных значений частотной характеристики W (jω) по передаточной функции W (S) звена, заданной векторами коэффициентов ее числителя (b) и знаменателя (а), а также по заданному вектору W частоты со. Если аргумент W не указан, процедура автоматически выбирает 200 отсчетов частоты, для которых вычисляется частотная характеристика.
Если не указана выходная величина, т.е. обращение имеет вид:
freqs (b, a, W), то процедура выводит в текущее графическое окно два графика - АЧХ и ФЧХ. Рассмотрим следующий пример: пусть для передаточной функции (4.13) выбраны такие значения параметров:
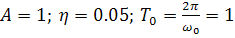
Вычислим значения коэффициентов числителя и знаменателя и выведем графики АЧХ и ФЧХ:
>>Т0= 1; dz = 0.05;
>>om0 = 2*pi/T0; А= 1;
>>a1(1)=l; а1(2) = 2*dz*om0; al(3) = om0^2; b1(1) = А;
>>freqs (b1,a1)

Допустим, что заданный процесс x(t) представлен в виде отдельных его значений в дискретные моменты времени, которые разделены одинаковыми промежутками Ts времени (дискретом времени Ts). Обозначим через х(k) значение процесса в момент времени t = k*Ts, где k - номер измерения с начала процесса.
Запишем уравнение (4.12) через конечные разности процессов х и у, учитывая, что конечно-разностным эквивалентом производной 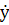 является конечная разность.
является конечная разность.
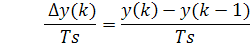
Эквивалентом производной 2-го порядка у является конечная разность 2-го порядка:
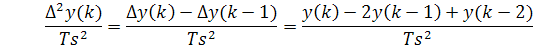
Тогда получим разностное управление:

Применим к уравнению (3) Z - преобразования:
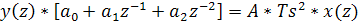 (4.15)
(4.15)
 (4.16)
(4.16)
Дискретная передаточная функция фильтра определяется из уравнения (4.15):
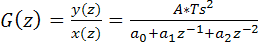 (4.17)
(4.17)
Таким образом, цифровым аналогом ранее введенного колебательного звена является цифровой фильтр с коэффициентами числителя и знаменателя, рассчитанными по формулам (4.16) и (4.17):
>>T0=l; dz=0.05; Ts=0.01;
>>om0=2*pi/T0; A=l; omS=om0*Ts;
>>a(l)=l+2*dz*omS+omS^2;
>>a(2)=-2*(l+dz*omS);
>>a(3)=l;
>>b(1)=A*Ts*Ts*(2*dz*om0^2);
Чтобы получить частотную дискретную характеристику G(ejω) по дискретной передаточной функции G(z), заданной векторами значений её числителя b и знаменателя а, нужно использовать процедуру freqz, обращение к которой аналогично обращению к процедуре freqz: freqz(b, а)
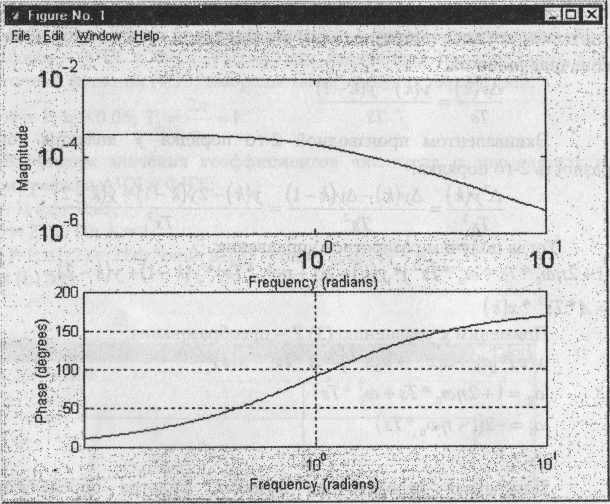
Фильтрация, т.е. преобразование заданного сигнала с помощью линейного фильтра, описываемого дискретной передаточной функцией вида:
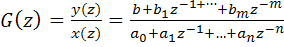 (4.18)
(4.18)
осуществляется процедурой filter следующим образом:
y=filter (b, а, х), где:
х - заданный вектор значений входного сигнала,
у - вектор значений выходного сигнала фильтра, получаемого вследствие фильтрации,
b - вектор коэффициентов числителя дискретной передаточной
функции (4.7) фильтра;
а - вектор коэффициентов знаменателя этой функции.
В качестве примера рассмотрим следующую задачу:
Пусть требуется получить достаточно верную информацию о
некотором полезном сигнале, имеющем синусоидальную форму с
известным периодом Т1 = 1с и амплитудой А1 = 0.75.
Сформируем этот сигнал как вектор его значений в дискретные моменты времени с дискретом Ts = 0.001 с:
>>Те = 0.001;
>>t = 0: Ts: 20;
>>A1 =0.75;Т1 = 1;
>>Yp = A1*sin (2*pi*t/T1);
>>plot (t(10002: end), Yp (10002: end)), grid, ...
set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)
>>title ('Полезный процесс');
>>xlabel ('Время(с)');
>>ylabel ('Yp(t)');
Допустим, что вследствие прохождения через ПП (первичный преобразователь) к полезному сигналу добавился шум ПП в виде более высокочастотной синусоиды с периодом Т2=0.2с и амплитудой А2=5, а в результате измерения к нему еще добавился белый гауссов шум измерителя с интенсивностью Аш=5. В результате создается такой сигнал x(t):
>>Т2=0.2; А2=10; eps=pi/4;
>>Ash=5;
>>х=А1 *sin (2*pi*t./T1)+A2.*sin (2*pi.*t./T2+eps)+...
Ash*randn (1 .length (t));
>>plot (t (10002: end), x (10002: end)), grid, Set (gca, 'FontName', ...
'ArialCyr', 'FontSize', 16),
>>title ('Входной процесс');
>>xlabel ('Время (с)');
>>ylabel ('x(t)')
Требуется так обработать измеренные данные х, чтобы восстановить по ним полезный процесс как можно точнее.
Так как частота полезного сигнала известна заранее, то его восстановление можно осуществить при помощи резонансного фильтра отмеченного выше вида. При этом необходимо создать такой фильтр, чтобы период его собственных колебаний Тф был равен периоду колебаний полезного сигнала (Тф=Т1). Чтобы после прохождения через такой фильтр амплитуда восстановленного сигнала совпадала с амплитудой полезного сигнала, нужно входной сигнал фильтра домножить на постоянную величину 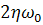 (т.к. при резонансе амплитуда выходного сигнала «уменьшается» именно во столько раз по сравнению с амплитудой входного сигнала).
(т.к. при резонансе амплитуда выходного сигнала «уменьшается» именно во столько раз по сравнению с амплитудой входного сигнала).
1) Сформируем фильтр, описанный выше:
>>Т1 =l;Tf=T1;dz = 0.05;
>>om0 = 2*pi/Tf; А = 1; omS = om0*Ts;
>>a(1) = 1+2*dz*omS+omS^2;
>>a(2) = -2*(l+dz*omS);
>>а(3)=1;
>>b(1) - A*Ts*Ts*(2*dz*om0^2);
2) Пропустим сформированный процесс через него:
>>у = filter (b, а, х)
>>plot (t(10002: end), у(10002: end), t(10002: end), Yp(10002: end)), grid,
>>title ('Процесс на выходе фильтра (Tf = 1; dz = 0.05)');
>>хlabel('Время(с)');
>>ylabel('Y(t)');
В результате получим восстановленный процесс. Соответствие хорошее, но более точному восстановлению препятствуют два обстоятельства:
1. Восстановленный процесс восстанавливается на выходе фильтра только спустя некоторое время вследствие нулевых начальных условий самого фильтра как динамического звена. Это можно увидеть:
>>у = filter (b, а, х)
>>plot (t, у, t, Yp), grid, set(gca, 'FontName', 'ArialCyr', 'FontSize', 16)
>>title ('Процесс на выходе фильтра (Tf = 1; dz = 0.05)');
>>хlabel('Время(с)');
>>ylabel('Y(t)');
2. В установившемся режиме наблюдается значительный сдвиг (тг/2) фаз между восстанавливаемым и восстановленным процессами; это понятно, т.к. при резонансе сдвиг фаз между входным и выходным процессами достигает именно тс/2.
3.Чтобы избежать фазовых искажений полезного сигнала при его восстановлении, можно воспользоваться процедурой двойной фильтрации - filtfilt. Обращение к ней имеет такую же форму, что и к процедуре filter. В отличие от filter процедура filtfilt осуществляет обработку вектора х в два приёма: сначала в прямом, а затем в обратном направлении:
>>у = filtfilt (b, а, х)
>>plot (t, у, t, Yp), grid, set (gca, 'FontName', 'Arial Cyr', 'FontSize', 16)
>>title ('Применение процедуры FILTFILT');
>>xlabel ('Время (с)');
>>ylabel ('Y(t)');
Дата добавления: 2016-02-04; просмотров: 1082;
