Формирование случайных процессов
В соответствии с теорией случайных процессов сформировать случайный процесс с заданной корреляционной функцией можно, если сначала сформировать случайный процесс, являющийся нормально (гауссов закон) распределённым белым шумом, а затем «пропустить» его через некоторое динамическое звено (формирующий фильтр). На выходе получается нормально распределённый случайный процесс с корреляционной функцией, вид которой определяется типом формирующего фильтра как динамического звена.
Белый гауссов шум образуется при помощи процедуры randn. Для этого нужно задать дискрет времени Ts, затем образовать с этим шагом массив (вектор) t моментов времени в нужном диапазоне, а затем сформировать по указанной процедуре вектор-столбец длиной, равной длине вектора t, например:
>>Ts = 0.01;
>>t = 0: Ts: 20;
>>xl = rand (1, length(t));
>>plot (t, x1), grid, set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)
>>title ('Входной процесс - белый шум Гаусса (Ts = 0.01)');
>>хlabеl('Время(с)');
>>ylabel('x1(t)');
Проделаем эту процедуру с Ts = 0.001 с (x2(t))
Создадим дискретный фильтр 2-го порядка с частотой собственных
колебаний 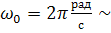 1 Гц и относительным коэффициентом затухания η=0.05 по формулам (4.16) коэффициентов:
1 Гц и относительным коэффициентом затухания η=0.05 по формулам (4.16) коэффициентов:
>>om0 = 2*pi; dz = 0.05; А = 1; omS = om0*Ts;
>>а(1) = 1+2*dz*omS + omS^2;
>>a(2) = -2*(1+dz*omS);
>>a(3)= 1;
>>b(1)=A*2*dz*omS^2;
Пропустим образованный процесс x1(t) через созданный фильтр:
>>y1=filter (b, a, x1);
Построим график процесса y1(t) на выходе фильтра:
>>plot (t,y1), grid, Set (gca, 'FontName', 'ArialCyr', 'FontSize', 16)
>>title ('Процесс на выходе фильтра (Т0=1; dz=0.05, Ts=0.01)';
>>xlabel ('Время (с)');
>>ylabel ('Y1(t)')
Аналогичные операции произведем с процессом x2(t):
>>Ts=0.01
>>om0 = 2*pi; dz = 0.05; A = 1; omS = omO*Ts;
>>a(1) = l+2*dz*omS + omS^2;
>>a(2) = -2*(1+dz*omS);
>>a(3)= 1;
>>b(1) = A*2*dz*omS^2;
>>у1=filter (b, a, x2); t=0: Ts: 20;
>>plot (t,y1), grid;
>>Set (gca, 'FontName', 'ArialCyr', 'FontSize', 14)
>>title ('Процесс на выходе фильтра (Т0=1; dz=0.05, Ts=0.01)';
>>xlabel ('Время (с)');
>>ylabel ('Y2 (t)')
На выходе формирующего фильтра образуется случайный процесс с преобладающей частотой 1 Гц.
Спектральная плотность мощности (СИМ (или СП))
В теории случайных процессов СПМ определяется как Фурье-изображение корреляционной функции R12(t) и применяется в основном для двух одновременно протекающих стационарных процессов x1(t) и x2(t). Взаимная корреляционная функция (ВКФ) двух таких процессов
определяется соотношением:
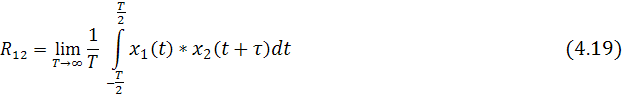
То есть ВКФ является средним во времени значением произведения 1-й функции на сдвинутую относительно неё на время задержки τ вторую функцию.
Таким образом, взаимная спектральная плотность (ВСП) двух стационарных процессов может быть определена следующим образом:

При численных расчётах, когда оба процесса x1(t) и x2(t) заданы на определённом ограниченном промежутке времени Т своими значениями в некоторых точках, разделённых дискретом времени Ts, формулу (4.19) можно трансформировать в следующую:
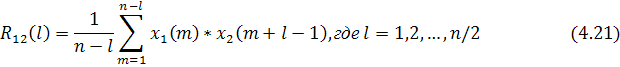
или более простое соотношение:
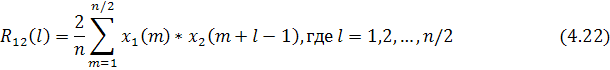
а вместо (4.20) использовать:
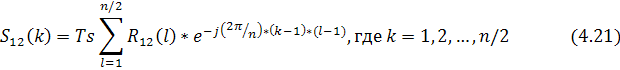
Подставим (4.22) в (4.23) и изменим в нём порядок суммирования, тогда придём к соотношению между ВСП и результатами преобразований процедурой fft заданных измеренных значений процессов:
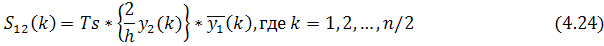
где 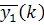 - комплексно сопряжённое значение
- комплексно сопряжённое значение 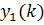 .
.
С учётом соотношений (4.10) и (4.11) выражение (4.24) можно представить в виде:

ВСП 2-х процессов при любом значении частоты равна произведению значения комплексного спектра 2-го процесса на комплексно-сопряжённое значение Фурье-изображения 1-го процесса на той же частоте.
Формулы (4.10) и (4.11) и (4.25) являются математической основой для вычисления в MatLAB соответственно Фурье-изображения процесса, его комплексного спектра и взаимной спектральной плотности 2-х процессов.
Дата добавления: 2016-02-04; просмотров: 1077;
