Приемы детерминированного факторного анализа
Важнейшим вопросом в экономическом анализе является изучение и измерение влияния отдельных факторов на величину исследуемых экономических показателей. Без глубокого и всестороннего изучения факторов нельзя обосновывать будущие планы и применять правильные управленческие решения, а также выявлять резервы повышения эффективности производства.
Все множество факторов, воздействующих на экономические явления и процессы классифицируют по следующим признакам:
- по отношению к исследуемому объекту:
а) внешние факторы – те, которые не зависят от деятельности предприятия (инфляция, коньюнктура рынка и т.д.);
б) внутренние факторы – те, которые отражают вклад предприятия в изменение тех или иных показателей.
- по характеру воздействия:
а) экстенсивные – связанные с количественным приростом результативного показателя (увеличение выпуска численности продукции за счет наращивания численности);
б) интенсивные – связанные с качественным приростом результативного показателя (за счет увеличения производительности труда).
- при измерении степени влияния факторов на результаты хозяйственной деятельности:
а) количественные, структурные и качественные;
б) простые (например, количество рабочих дней) и сложные (например, выработка);
в) измеряемые и неизмеряемые (например, уровень подготовки кадров);
г) прямые (факторы 1-го порядка) и косвенные (факторы 2-го и более высокого порядка).
Методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей называется факторным анализом.
Факторный анализ основывается на моделировании.
Моделирование – это процедура создания аналога объекта исследования. Применительно к экономике под моделированием понимают установление количественной зависимости между показателями, которая получает математическое выражение, т.е. результатом моделирования является аналитическая модель, которая отражает зависимость показателя от его факторов.
В факторном анализе различают модели детерминированные (функциональные) и стохастические (вероятностные, корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами).
В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей:
1. Аддитивные модели:
y = a + b + с +…
Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторов.
2. Мультипликативные модели:
y = a * b * с *…
Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов.
3. Кратные модели:
y = a/b
Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого.
4. Смешанные (комбинированные) модели:
y = a(b + c); y = a/(b + c); y = (a + b)/c и т.д.
Это сочетание в различных комбинациях предыдущих моделей.
Для определения влияния отдельных факторов на прирост результативных показателей в детерминированном анализе используются следующие способы:
Способ цепных подстановок
Способ цепных подстановок состоит в последовательной замене базисной величины одного из факторов на его фактическую величину в изучаемом периоде.
Основные правила применения способа цепных подстановок заключаются в следующем:
1) Расчет влияния факторов начинают с количественных, затем рассчитывают влияние структурных факторов и, в последнюю очередь, качественных.
2) Для расчета влияния отдельных факторов на результативный показатель строят так называемые “подстановки”. Количество этих “подстановок” всегда меньше на единицу, чем количество факторов в модели.
3) При построении “подстановки” если влияние какого-либо фактора еще не определено, то его величина на данном этапе расчетов берется на уровне базисного периода, а если же влияние фактора определяется на данном этапе или оценивалась раннее, то его величина берется на уровне анализируемого периода.
Алгоритм расчетов влияния отдельных факторов на результативный показатель способом цепных подстановок имеет вид:
1.для мультипликативной модели
y = a*b*c,
в которой a и b – количественные факторы; с – качественный.
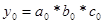 - значение показателя в базисном периоде;
- значение показателя в базисном периоде;
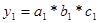 - значение показателя в отчетном периоде.
- значение показателя в отчетном периоде.
Выполняем “подстановки”:
Первая «подстановка»: 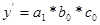
Вторая «подстановка»: 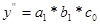
Рассчитываем влияние факторов:
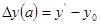
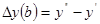
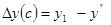
2.для кратной модели
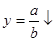 ,
,
в которой а – количественный фактор; b – качественный.
Выполняем «подстановку»:
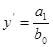
Рассчитываем влияние факторов:
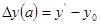
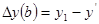
У данного способа есть достоинства и недостатки.
Достоинства:
- способ применяется для любого вида детерминированных моделей;
Недостатки:
- важен порядок расчета влияния факторов;
- громоздкость расчетов.
Способ абсолютных разниц
Способ абсолютных разниц является модификацией способа цепных подстановок и требует меньшего количества расчетов.
Алгоритм расчетов влияния отдельных факторов на результативный показатель способом абсолютных разниц имеет вид:
1.Для мультипликативной модели
y = a*b*c,
в которой a, b – количественные факторы; с – качественный.
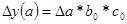
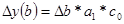
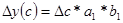
2.Для аддитивных моделей
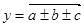
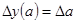
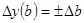
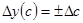
Интегральный способ
Особенности данного способа в том, что для каждого вида моделей свой алгоритм. Достоинством является то, что не важен порядок расчета влияния факторов. Недостаток: ограниченность в применении (для мультипликативных, кратных и некоторых смешанных моделей)
Алгоритм расчетов влияния отдельных факторов на результативный показатель индексным способом имеет вид:
1.Для мультипликативной модели
y = а * b
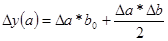
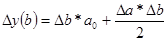
2.Для мультипликативной модели
у = a*b*c
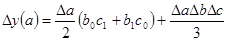
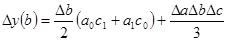
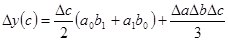
3.Для кратной модели
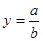
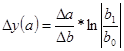
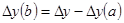
Индексный способ
Индексный способ применим для мультипликативных и кратных моделей. Данный способ наряду со способом цепных подстановок и способом абсолютных разниц требует определенной последовательности расчетов. Расчеты следует начинать с оценки влияния количественных, затем структурных и качественных факторов.
Для мультипликативной факторной модели
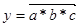 ,
,
в которой a,b – количественные факторы; c - качественный
алгоритм расчетов по оценке влияния отдельных факторов индексным способом имеет вид:
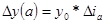 , где
, где 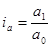 ,
, 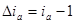
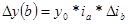
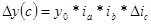
Способ логарифмирования
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. Алгоритм расчетов имеет вид:
у = a*b*c
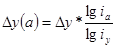
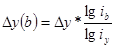
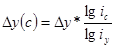
Способ долевого участия
Данный способ применим только для аддитивных моделей. Алгоритм расчетов имеет вид:
у = a+b+c
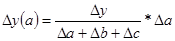
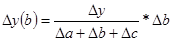
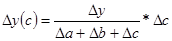
Дата добавления: 2016-02-04; просмотров: 1355;
