Приемы математической статистики, применяемые для анализа связей между показателями

Для изучения косвенных, непосредственных, вероятностных связей, когда невозможно построить детерминированную модель, применяются методы математической статистики.

Изучаются эти связи с помощью стохастического анализа.

К основным методам математической статистики, которые применяются для анализа стохастических моделей, относятся:

1. Корреляционный анализ – это метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону.

В основе метода лежит расчет коэффициента корреляции.

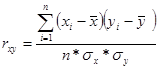
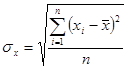
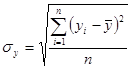
Границы коэффициента корреляции: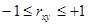

Если:

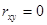, то связь между показателями отсутствует;

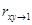, связь линейная, прямая;

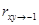, связь линейная, обратная.

2. Регрессионный анализ – это метод установления аналитического выражения статистической зависимости между исследуемыми признаками. В основе метода лежит построение уравнения регрессии. В случае прямолинейной связи между двумя показателями уравнение регрессии имеет вид:

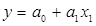
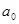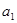Для того, чтобы определить параметры уравнения регрессии и , необходимо решить систему нормальных уравнений:

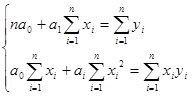
Уравнения регрессии позволяют прогнозировать значение результирующего признака при заданном факторном.

3. Кластерный анализ – метод многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками.

4. Дисперсионный анализ – это метод позволяющий подтвердить или опровергнуть гипотезу о том, что 2 выборки данных относятся к одной генеральной совокупности.