Маркетинговый анализ оценки факторов. Индексный метод. Факторный анализ.

Индексный метод.Индексный метод дает возможность успешно решать целый ряд задач маркетингового анализа, которые требуют сопоставления сложных, многофакторных явлений и процессов во времени и в пространстве [11].

Расчет индивидуальных индексов цен и физического объема.

В зависимости от степени охвата элементов совокупности индексы подразделяются на индивидуальные и общие (групповые). Индивидуальные индексы характеризуют относительное изменение значений признака у отдельных элементов (единиц) совокупности в сравниваемых периодах.

Для определения относительного изменения цен (p) по каждому товару необходимо рассчитать индивидуальные индексы цен (i_p) по формуле [12]

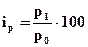, (2)

где p₀ и p₁ – цена товара в базисном и отчетном периодах.

Для определения относительного изменения количества продажи каждого вида товара (q) необходимо рассчитать индивидуальные индексы физического объема (i_q) по формуле

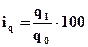, (3)

где q₀ и q₁ – количество (физический объем) товара, реализованного в базисном и отчетном периодах.

Построение, расчет и анализ агрегатного индекса физического объема товарооборота

Для определения относительного изменения количества реализованных товаров по совокупности (двум разнородным товарам) рассчитывают агрегатный индекс физического объема товарооборота.

В маркетинговом анализе часто приходится сталкиваться с изучением изменения объемов произведенной, проданной или потребленной продукции в ее натурально-вещественной форме. Объемы этой разнородной продукции непосредственно суммировать нельзя. Для характеристики относительного изменения общего объема такой продукции строят специальные показатели – агрегатные индексы физического объема, т.е. агрегатные индексы объемных показателей. Таким образом, с помощью агрегатных индексов сравнивают совокупности (социально-экономические явления), состоящие из элементов, не поддающихся непосредственному суммированию.

Преодоление несуммарности отдельных элементов изучаемой совокупности, состоящей из разнородных товаров, достигают путем введения в индекс дополнительного показателя, экономически тесно связанного с индексируемым показателем. Этот дополнительный показатель называют весом агрегатного индекса. Таким образом, агрегатный индекс состоит из двух элементов – индексируемого (изменяемого) показателя и веса индекса (неизменяемого показателя).

Относительное изменение физического объема товарооборота по всей совокупности товаров (по двум товарам вместе) определяют путем расчета агрегатного индекса физического объема.

В агрегатном индексе физического объема индексируемым (изменяемым) показателем является количество проданного товара (q), а весом индекса (неизменяемым показателем) – цена товара (p).

Агрегатный индекс физического объема рассчитывают по формуле:

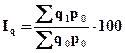, (4)

где 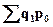– стоимость реализованных товаров (товарооборот) в отчетном периоде по ценам базисного периода,

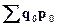– стоимость реализованных товаров (товарооборот) в базисном периоде.

Агрегатный индекс физического объема показывает, как в среднем изменился физический объем товарной массы, измеренный в ценах базисного периода, в отчетном периоде по сравнению с базисным периодом по всей совокупности разнородных товаров.

Агрегатный индекс физического объема может быть рассчитан и по весам отчетного периода, т.е. как отношение товарооборота отчетного периода к товарообороту базисного периода, выраженного в ценах отчетного периода, по формуле:

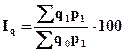(5)

Построение, расчет и анализ агрегатного индекса цен

С совокупностями, состоящими из непосредственно несуммируемых элементов, приходится сталкиваться и тогда, когда необходимо получить сводную характеристику относительного изменения общего уровня цен, т.к. уровни цен отдельных (разнородных) товаров суммировать нельзя.

Относительное изменение цен по совокупности в целом (в нашем примере по двум разнородным товарам вместе) определяют путем расчета агрегатного индекса цен, т.е. агрегатного индекса качественного показателя.

В агрегатном индексе цен индексируемым (изменяемым) показателем является цена товара (р), а весом индекса (неизменяемым показателем) – количество (физический объем) товара (q).

Агрегатный индекс цен рассчитывают двумя методами.

Первый метод – Агрегатный индекс цен строят по весам отчетного периода (q₁). Такой индекс называют агрегатным индексом цен Пааше:

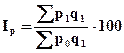, (6)

где 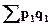–стоимость реализованных товаров (товарооборот) в отчетном периоде,

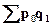– стоимость реализованных товаров (товарооборот) в отчетном периоде по ценам базисного периода.

Разность между числителем и знаменателем агрегатного индекса цен характеризует абсолютную сумму экономии (переплаты) в результате снижения (повышения) цен, т.е.

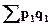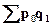– (7)

Второй метод – в расчет агрегатного индекса цен берут веса базисного периода, т.е. q₀:

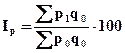, (8)

где 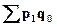– стоимость реализованных товаров (товарооборот) в базисном периоде по ценам отчетного периода,

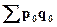– стоимость реализованных товаров (товарооборот) в базисном периоде по ценам отчетного периода.

Общий индекс цен, рассчитанный по формуле 8, называют индексом Ласпейреса.

Агрегатные индексы цен, рассчитанные разными методами, дают и разные результаты. Это объясняется тем, что индекс цен Пааше рассчитывается исходя из объема и структуры товаров, реализованных в отчетном периоде, а индекс цен Ласпейреса определяется по объему и структуре товаров, реализованных в базисном периоде.

Построение, расчет и анализ среднего арифметического взвешенного и среднего гармонического взвешенного индексов

Для расчета агрегатного индекса физического объема товарооборота и агрегатного индекса цен необходимы данные о количестве реализованных товаров в натуральном измерении. В случае отсутствия таких данных для расчета сводных обобщающих относительных показателей изменения объемного и качественного признаков используют среднюю арифметическую и среднюю гармоническую форму общих индексов. Формулы таких индексов получают путем преобразования агрегатных индексов в средние через индивидуальные индексы.

Для определения относительного изменения физического объема товарооборота обычно рассчитывают агрегатный индекс физического объема товарооборота .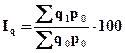

Для преобразования агрегатного индекса физического объема в средний арифметический взвешенный используют формулу индивидуального индекса физического объема 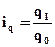, из которой следует, что q₁=i_q*q₀. Далее в числителе агрегатного индекса заменяют q₁ на выражение i_q*q₀. Тогда формула индекса физического объема принимает следующий вид:

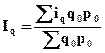, (9)

где i_q – индивидуальный индекс физического объема;

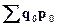– стоимость реализованных товаров (товарооборот) в базисном периоде.

В таком виде агрегатный индекс физического объема выступает как средняя арифметическая величина из индивидуальных индексов физического объема , взвешенных по стоимости товаров базисного периода (товарообороту базисного периода) – q₀p₀.

Для изучения относительного изменения уровня цен на разнородные товары в отчетном периоде по сравнению с базисным периодом обычно рассчитывают агрегатный индекс цен по формуле (6), т.е.:

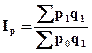
Если отсутствуют данные о товарообороте отчетного периода в ценах базисного периода, то используют формулу индивидуального индекса цен 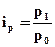, из которой следует, что 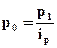. Далее в знаменателе агрегатного индекса цен заменяют p₀ на выражение 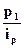. Тогда формула индекса цен принимает следующий вид:

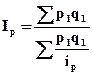(10)

В таком виде индекс цен выступает как средняя гармоническая величина из индивидуальных индексов цен, взвешенных по товарообороту отчетного периода ( ).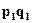

Оценка роли отдельных факторов в изменении сложного явления путем построения системы взаимосвязанных индексов.

Одним из направлений применения индексного метода является оценка роли отдельных факторов в изменении сложного явления. Под сложным явлением, в данном случае, понимают явление, изменение которого обусловлено действием нескольких факторов, выступающих как множители совокупного результата. К таким сложным явлениям может быть отнесена, например, стоимость реализованных товаров (товарооборот), изменение которой обусловлено изменением уровня цен и количества товаров (физического объема товарооборота).

Изменение товарооборота обусловлено совместным изменением физического объема товарооборота и цены. Индекс физического объема товарооборота (I_q) и индекс цен (I_z) выступают здесь как измерители роли этих факторов в общей динамике товарооборота (I_zq). Следовательно, эти индексы образуют единую индексную систему таким образом, что произведение индексов физического объема и цен должно давать показатель (индекс) изменения товарооборота (мультипликативная связь), т.е.

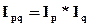(11)

или

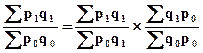(112)

где 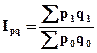(13) – индекс товарооборота, характеризующий относительное изменение товарооборота под влиянием изменения цен и физического объема товарооборота;

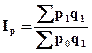(14) – индекс цен, характеризующий относительное изменение товарооборота под влиянием изменения цен;

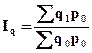(15) – индекс физического объема товарооборота, показывающий относительное изменение товарооборота под влиянием изменения физического объема товарооборота.

Для того чтобы произведение двух сопряженных индексов (I_p и I_q) давало индекс товарооборота (I_pq), необходимо веса (соизмерители) индексов брать на разных уровнях. Так, если в индексе цен весом выступает количество товаров (физический объем товарооборота) отчетного периода, то в индексе физического объема товарооборота количество товаров должно быть соизмерено по ценам базисного периода.

Относительное изменение товарооборота по совокупности товаров характеризует общий индекс товарооборота.