Определение абсолютного изменения среднего уровня цены – общее и под влиянием отдельных факторов.
На основе произведенных ранее расчетов индексов цен переменного состава, фиксированного состава, индекса структурных сдвигов может быть определено и абсолютное изменение средней по двум организациям цены в отчетном периоде по сравнению с базисным.
Абсолютное изменение средней цены под влиянием обоих факторов определяется (исходя из индекса переменного состава) как разность между средней по двум организациям ценой товара в отчетном периоде и средней ценой в базисном периоде:
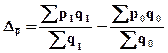 (28)
(28)
Абсолютное изменение средней цены под влиянием изменения уровня цен в каждой торговой организации (первый фактор) определяется (исходя из индекса фиксированного состава) как разность между средней по двум организациям ценой товара по двум организациям в отчетном периоде и условной средней ценой товара базисного периода, рассчитанной по структуре отчетного периода:
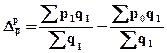 (29)
(29)
Абсолютное изменение средней цены под влиянием изменения доли каждой организации с разным уровнем цен в общем количестве реализованного товара (второй фактор) определяется (исходя из индекса структурных сдвигов) как разность между условной средней ценой товара базисного периода, рассчитанной по структуре отчетного периода, и средней ценой товара отчетного периода:
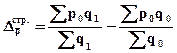 (30)
(30)
Абсолютные приросты (изменения) средней цены связаны между собой следующим образом:
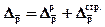 (31)
(31)
т.е. общий абсолютный прирост средней цены за счет двух факторов равен сумме абсолютного прироста средней цены, сформировавшегося под влиянием первого фактора, и абсолютного прироста, вызванного влиянием второго фактора (аддитивная связь).
Абсолютное изменение средней цены под влиянием двух факторов определяется по формуле:
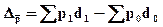 (32)
(32)
Абсолютное изменение средней цены под влиянием первого фактора определяется по формуле:
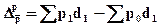 (33)
(33)
Абсолютное изменение средней цены под влиянием второго фактора определяется по формуле:
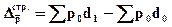 (34)
(34)
Подробный пример расчетов в соответствии с выше представленной методикой приведен в разделе практические задания.
Факторный анализ.
Факторный анализ – это набор методов и действий, используемый для выделения из множества наиболее значимых переменных – факторов и выявления взаимосвязей между выделенными факторами [13].
Целью факторного анализа является получение сводки информации, содержащей большое число количественных оценок, как правило метрических (или рейтинговых) шкал, в меньшее число суммарных величин, называемых факторами.
Чаще всего факторный анализ в маркетинговых исследованиях используют, когда проводится [14]:
– сегментация потребителей
– создание продукта
– разработка маркетинговой стратегии: стратегии позиционирования, стратегии коммуникации, медиа – стратегии и стратегии ценообразования.
Возможность соединить, или скомбинировать, число переменных вызывает необычайный интерес у исследователей. При этом они часто используют оценочные вопросы. Например, изучая отзывы посетителей об имидже магазинов оргтехники, необходимо создать общую концепцию «фирменного магазина», которая должна учитывать широту и глубину товарного ассортимента, гарантийное и техническое обслуживание, различные методы стимулирования сбыта.
Предположим, что менеджер магазина хотел бы создать имидж «фирменного магазина», но он понимает, что общее восприятие зависит от множества факторов. Если существует целая группа факторов, то они могут дополнять друг друга и повысить таким образом общую оценку восприятия магазина.
Рассмотрим основные принципы факторного анализа. В таблице 7 приведены оценки 6 респондентов, выставленные одному из магазинов оргтехники по 4 показателям.
Таблица 7 – Оценка магазина оргтехники шестью респондентами
| Респондент | Оценка магазина по следующим направлениям | |||
| Товарный ассортимент | Запасные комплектующие части | Предоставляемые скидки | Условия кредита | |
| В среднем | 4,5 | 3,83 | 2,33 | 1,5 |
По данным таблицы можно видеть, что респондент, выставляющий высокую оценку товарному ассортименту, также дает высокую оценку и разнообразию запасных комплектующих частей. Подобная взаимосвязь существует и между факторами «Предоставляемые скидки» и «Условия кредита». Итак, четыре оценки могут быть скомбинированы в две суммарные величины через усреднение парных оценок. В результате объединения образуются два обобщенных (укрупненных) фактора, которые можно назвать «Товарное предложение» и «Ценовое стимулирование сбыта» (таблица 8).
Таблица 8 – Средняя оценка двух укрупненных факторов
| Респондент | Товарное предложение | Ценовое стимулирование сбыта |
| 4,5 | 1,5 | |
| 3,5 | 1,5 | |
| 3,5 | 2,5 | |
| 5,0 | 2,0 | |
| 3,5 | 1,5 | |
| 5,0 | 2,5 | |
| В среднем | 4,25 | 1,92 |
Итак, два укрупненных фактора являются линейной комбинацией четырех исходных переменных. Природа вновь образованных факторов может быть определена с помощью так называемых факторных нагрузок.
Факторные нагрузки – это корреляция между обобщенным фактором и первоначальной переменной. Другими словами, нагрузку соответствующей переменной на конкретный фактор характеризует коэффициент корреляции. Если первоначальная переменная тесно связана с укрупненным фактором, то корреляция (или нагрузка) должна быть высокой.
Коэффициент корреляции может принимать значения от (-1) до (+1). Однако сам по себе знак факторных нагрузок не имеет внутреннего содержания и не несет информации о зависимости между переменной и фактором. Но следует сопоставлять между собой знаки для различных переменных при данном факторе. Целесообразно перед применением факторного анализа так задать переменные, чтобы знаки коэффициентов нагрузок на данный фактор были одинаковыми. Результаты расчетов факторных нагрузок приведены в таблице 9.
Таблица 9 – Факторные нагрузки
| Переменная | Корреляция | |
| с фактором 1 «Товарное предложение» | с фактором 2 «Ценовое стимулирование сбыта» | |
| Товарный ассортимент | 0,95 | 0,1 = (0,1х0,1) = 0,01 |
| Запасные и комплектующие части | 0,86 | 0,06 = (0,06 х0,06) = 0,0036 |
| Предоставляемые скидки | 0,96 | 0,81= (0,81х0,81) = 0,6561 |
| Условия кредита | 0,14 | 0,72 (0,72 х0,72) = 0,518 |
| Собственное число λ | 1,6873 | 1,1877 = (0,01+0,0036+0,6561+0,518) |
| Процент общей дисперсии | 42,18 | 29,7 |
Сумма квадратов факторных нагрузок называется собственным числом λ, которое используется как критерий определения числа факторов и как мера дисперсии, соответствующая данному фактору.
В факторном анализе могут рассматриваться от одного до нескольких факторов, но их максимальное число должно быть равно числу переменных. Решение о количестве факторов принимается на основе процента вариации в первоначальных данных, объясненных каждым фактором.
Процент общей дисперсии, соответствующий укрупненному фактору, определяется как отношение собственного числа i-го фактора к сумме всех собственных чисел λ, равной количеству первоначальных переменных:
В рассматриваемом случае (таблица 9) фактор 1 объясняет 42,18% общей вариации (1,6873: 4 = 0,4218), а фактор 2 – 29,70%. Оба фактора объясняют 71,88% вариации по всем четырем оценкам (42,18 + 29,70). То есть больше всего влияния оказывает первый фактор.
Дата добавления: 2016-01-29; просмотров: 1960;
