Симметричный обход BST

Бинарные деревья поиска обладают чрезвычайно полезным свойством при симметричном обходе. Напомним, при симметричном обходе сначала рекурсивно посещается левое поддерево, затем узел-родитель, затем правое поддерево. Характеристическое свойство, использованное при построении дерева, при таком способе обхода обеспечивает упорядоченность ключей по возрастанию:

0 1 2 3 4 5 6 7 8 9

Это свойство бинарных деревьев поиска может быть использовано как один из способов сортировки данных. Чтобы вывести какие-либо данные в отсортированном порядке, достаточно построить из них дерево бинарного поиска, а затем обойти симметрично, формируя последовательность-результат.

Ниже приведено объявление и реализация симметричного обхода BST:

bstree.hpp:

// ...

typedef void( * BSTreeWalkFunction ) ( constBSTree::Node & _node );

voidBSTreeSymmetricWalk ( constBSTree & _tree, BSTreeWalkFunction _f );

// ...

bstree.cpp:

// …

// Вспомогательная функция симметричного обхода поддерева

voidBSTreeSymmetricWalk ( constBSTree::Node * _pNode, BSTreeWalkFunction _f )

{

// Проверка на пустую ветку

if( ! _pNode )

return;

// Обход левого поддерева

BSTreeSymmetricWalk( _pNode->m_pLeft, _f );

// Посещение текущего родительского узла

( * _f )( * _pNode );

// Обход правого поддерева

BSTreeSymmetricWalk( _pNode->m_pRight, _f );

}

// Симметричный обход дерева

voidBSTreeSymmetricWalk ( constBSTree & _tree, BSTreeWalkFunction _f )

{

BSTreeSymmetricWalk( _tree.m_pRoot, _f );

}

Учитывая такое свойство, реализация поиска минимального и максимального ключа в дереве становится тривиальной - достаточно найти самый левый и самый правый узел в дереве соответственно:

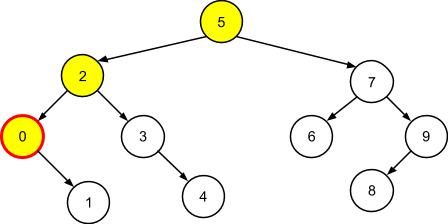
// Поиск узла с минимальным ключом - на каждом шаге движемся по левому поддереву:

BSTree::Node * BSTreeMinimumNode ( BSTree::Node * _pNode )

{

assert( _pNode );

BSTree::Node * pCurrent = _pNode;

while( pCurrent && pCurrent->m_pLeft )

pCurrent = pCurrent->m_pLeft;

returnpCurrent;

}

// Поиск минимального ключа - извлекаем из узла с минимальным ключом

intBSTreeMinimum ( constBSTree & _tree )

{

BSTree::Node * pMinimumNode = BSTreeMinimumNode( _tree.m_pRoot );

returnpMinimumNode->m_key;

}

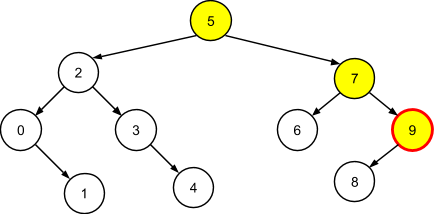
// Поиск узла с максимальным ключом - на каждом шаге движемся по правому поддереву:

BSTree::Node * BSTreeMaximumNode ( BSTree::Node * _pNode )

{

assert( _pNode );

BSTree::Node * pCurrent = _pNode;

while( pCurrent && pCurrent->m_pRight )

pCurrent = pCurrent->m_pRight;

returnpCurrent;

}

// Поиск максимального ключа - извлекаем из узла с максимальным ключом

intBSTreeMaximum ( constBSTree & _tree )

{

BSTree::Node * pMaximumNode = BSTreeMaximumNode ( _tree.m_pRoot );

returnpMaximumNode >m_key;

}