Массив меток и заголовок со списками дочерних узлов.

В этом альтернативном подходе дерево вместо массива индексов родительских узлов хранит для каждого узла-родителя последовательности дочерних узлов. Поскольку в общем случае число сыновей у различных узлов-родителей может колебаться, обычно для хранения последовательностей дочерних узлов используются связные списки.

Эта структура также предполагает изначальную фиксацию количества узлов в дереве.

structTree

{

// Количество узлов в дереве

intm_nNodes;

// Массив меток узлов, тип выбирается в зависимости от задачи

char* m_pNodeLabels;

// Структура, представляющая элемент связного списка индексов дочерних узлов

structChildIndexElement

{

intm_childIndex;

ChildIndexElement * m_pNext;

};

// Заголовок - указатели на первые элементы список дочерних узлов

ChildIndexElement ** m_pHeader;

};

Ниже показано графическое представление состояния реализованной структуры данных после формирования дерева-примера.

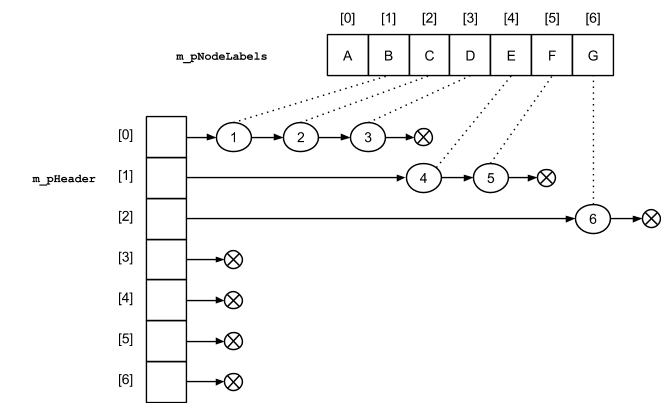
Функция создания дерева из N узлов реализуется следующим образом (за исключением заголовка вместо массива индексов родительских узлов - идентично предыдущей структуре данных:

Tree * TreeCreate ( int_nNodes )

{

// Число узлов должно быть положительным

assert( _nNodes > 0 );

// Создаем объект-дерево в динамической памяти

Tree * pTree = newTree;

pTree->m_nNodes = _nNodes;

// Создаем массив меток

pTree->m_pNodeLabels = newchar[ _nNodes ];

memset( pTree->m_pNodeLabels, 0, _nNodes );

// Создаем массив указателей на списки узлов-сыновей

pTree->m_pHeader = newTree::ChildIndexElement * [ _nNodes ];

memset( pTree->m_pHeader, 0, sizeof( Tree::ChildIndexElement * ) * _nNodes );

// Возвращаем созданное дерево

returnpTree;

}

Функция освобождения памяти чуть усложняется из-за работы с динамически выделяемыми элементами списков индексов дочерних узлов:

voidTreeDestroy ( Tree * _pTree )

{

// Уничтожаем метки узлов

delete[] _pTree->m_pNodeLabels;

// Уничтожаем списки узлов-сыновей

for( inti = 0; i < _pTree->m_nNodes; i++ )

{

Tree::ChildIndexElement * pCurrent = _pTree->m_pHeader[ i ];

while( pCurrent )

{

Tree::ChildIndexElement * pTemp = pCurrent->m_pNext;

deletepCurrent;

pCurrent = pTemp;

}

}

// Уничтожаем массив указателей на списки узлов-сыновей

delete[] _pTree->m_pHeader;

// Уничтожаем само дерево

delete_pTree;

}

Функции получения индекса корневого узла и работы с метками узлов реализуются полностью идентично структуре с массивом индексов родительских узлов.

Данная структура уменьшает вычислительную сложность реализации операции LEFTMOST_CHILD с линейной до константной за счет специальных структурных связей от родителя к дочерним узлам:

intTreeGetLeftmostChildIndex ( constTree & _tree, int_nodeIndex )

{

assert( _nodeIndex < _tree.m_nNodes );

Tree::ChildIndexElement * pCurrent = _tree.m_pHeader[ _nodeIndex ];

returnpCurrent ? pCurrent->m_childIndex : -1;

}

Зная родительский узел, для реализации перебора дочерних узлов слева направо необходимо лишь последовательно пройти по связному списку, на первый элемент которого указывает соответствующая узлу-родителю ячейка заголовка.

Напротив, обратная задача получения индекса родительского узла по индексу дочернего в данной реализации усложняется от константной вычислительной сложности до линейной, поскольку прямых структурных связей более не предусмотрено, и поиск будет осуществляться сканирование списков дочерних узлов всех вышестоящих по иерархии узлов-родителей:

intTreeGetParentIndex ( constTree & _tree, int_nodeIndex )

{

// Проверяем корректность индекса

assert( _nodeIndex < _tree.m_nNodes );

// Ищем родительский узел, перебирая все списки сыновей

for( inti = 0; i < _nodeIndex; i++ )

{

Tree::ChildIndexElement * pCurrent = _tree.m_pHeader[ i ];

while( pCurrent )

{

if( pCurrent->m_childIndex == _nodeIndex )

// Искомый узел найден, соответственно, это был список узла-родителя

returni;

pCurrent = pCurrent->m_pNext;

}

}

// Родительский узел не найден

return-1;

}

Аналогично, не имея индекса родительского узла, получение индекса ближайшего правого братского узла также усложняется до линейного поиска:

intTreeGetRightSiblingIndex ( constTree & _tree, int_nodeIndex )

{

// Проверяем корректность индекса

assert( _nodeIndex < _tree.m_nNodes );

// Ищем родительский узел, перебирая все списки сыновей

for( inti = 0; i < _nodeIndex; i++ )

{

Tree::ChildIndexElement * pCurrent = _tree.m_pHeader[ i ];

while( pCurrent )

{

if( pCurrent->m_childIndex == _nodeIndex )

{

// Искомый узел найден, соответственно, это был список узла-родителя.

// Следующий узел-сын известен по непосредственной структурной связи

Tree::ChildIndexElement * pNext = pCurrent->m_pNext;

returnpNext ? pNext->m_childIndex : -1;

}

pCurrent = pCurrent->m_pNext;

}

}

// Братский узел не найден

return-1;

}

Ниже приведена процедура создания связи между указанными родительским и дочерними узлами. Предполагается помещение индекса дочернего узла в конец списка, соответствующего ячейке родительского узла в заголовке дерева. Если список ранее был пуст, его необходимо создать.

voidTreeSetParentIndex ( Tree & _tree, int_nodeIndex, int_parentIndex )

{

// Проверка корректности индексов

assert( _nodeIndex < _tree.m_nNodes );

assert( _parentIndex < _nodeIndex );

// Создаем новый узел-сын

Tree::ChildIndexElement * pNewElement = newTree::ChildIndexElement;

pNewElement->m_childIndex = _nodeIndex;

pNewElement->m_pNext = nullptr;

// Является ли этот узел первым сыном для родительского узла?

Tree::ChildIndexElement * pCurrent = _tree.m_pHeader[ _parentIndex ];

if( ! pCurrent )

{

// Да, формируем первый элемент списка узлов-сыноей

_tree.m_pHeader[ _parentIndex ] = pNewElement;

return;

}

// В противном случае, прикрепляем новый узел к концу списка

while( pCurrent->m_pNext )

pCurrent = pCurrent->m_pNext;

pCurrent->m_pNext = pNewElement;

}

Поскольку интерфейс функций, реализующих АТД “Дерево”, идентичен по сравнению с предыдущей рассмотренной структурой данных, то сформировать и обойти рассматриваемое дерево-пример способна та же самая тестовая программа без малейшей модификации.