Массив меток и массив родительских индексов.
В этом простейшем подходе дерево хранит:
· массив меток, соответствующих узлам по порядковым номерам;
· массив порядковых номеров узлов-родителей для каждого узла-потомка.
structTree
{
// Количество узлов в дереве
intm_nNodes;
// Массив меток узлов, тип выбирается в зависимости от задачи
char* m_pNodeLabels;
// Массив индексов родительских узлов
int* m_pParentIndices;
};
Предполагается, что количество узлов в дереве заранее известно и не меняется за время существования дерева, в противном случае такая структура неэффективна.
Графически рассматриваемый пример дерева можно представить следующим образом:
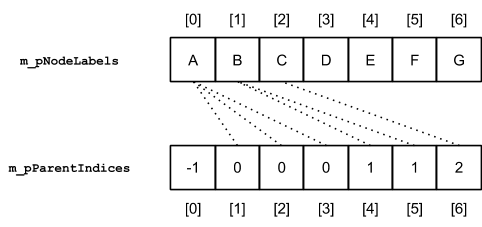
Для создания такой структуры данных необходимо:
1. Выделить память для самой структуры.
2. Выделить массив для хранения меток узлов и инициализировать значениями по-умолчанию.
3. Выделить массив для хранения индексов родительских узлов, и связать все узлы с корневым по умолчанию. Родителем корня пусть будет назначен несуществующий узел с индексом -1.
Tree * TreeCreate ( int_nNodes )
{
// Число узлов должно быть положительным
assert( _nNodes > 0 );
// Создаем объект-дерево в динамической памяти
Tree * pTree = newTree;
pTree->m_nNodes = _nNodes;
// Создаем массив меток
pTree->m_pNodeLabels = new char[ _nNodes ];
memset( pTree->m_pNodeLabels, 0, _nNodes );
// Создаем массив родительских индексов
pTree->m_pParentIndices = new int[ _nNodes ];
memset( pTree->m_pParentIndices, 0, _nNodes * sizeof( int) );
pTree->m_pParentIndices[ 0 ] = -1;
// Возвращаем созданное дерево
returnpTree;
}
Необходима соответствующая функция освобождения памяти дерева:
voidTreeDestroy ( Tree * _pTree )
{
// Уничтожаем метки узлов
delete[] _pTree->m_pNodeLabels;
// Уничтожаем массив родительских индексов
delete[] _pTree->m_pParentIndices;
// Уничтожаем само дерево
delete_pTree;
}
Корневой узел в такой структуре всегда размещается в нулевой позиции, в связи с чем операция ROOT имеет тривиальную реализацию (и вообще не использует конкретное дерево):
intTreeGetRootIndex ( constTree & )
{
return0;
}
Для работы с метками узлов необходима пара простых функций, скрывающих работу над внутренним массивом:
TreeNodeLabel TreeGetLabel ( constTree & _tree, int_nodeIndex )
{
assert( _nodeIndex < _tree.m_nNodes );
return_tree.m_pNodeLabels[ _nodeIndex ];
}
voidTreeSetLabel ( constTree & _tree, int_nodeIndex, TreeNodeLabel _label )
{
assert( _nodeIndex < _tree.m_nNodes );
_tree.m_pNodeLabels[ _nodeIndex ] = _label;
}
Также, не вызывает сложности запрос и модификация индекса родительского узла PARENT, поскольку данное отношение явно представлено в структуре дерева специальным массивом::
intTreeGetParentIndex ( constTree & _tree, int_nodeIndex )
{
assert( _nodeIndex < _tree.m_nNodes );
return_tree.m_pParentIndices[ _nodeIndex ];
}
voidTreeSetParentIndex ( Tree & _tree, int_nodeIndex, int_parentIndex )
{
assert( _nodeIndex < _tree.m_nNodes );
assert( _parentIndex < _nodeIndex );
_tree.m_pParentIndices[ _nodeIndex ] = _parentIndex;
}
В такой структуре данных операции ROOT, LABEL и PARENT имеют константную вычислительную сложность O(1), что свидетельствует об отличной приспособленности данной структуры данных к вышеуказанным операциям АТД “Дерево”.
В то же время, операции LEFTMOST_CHILD и RIGHT_SIBLING требуют прохода индексного массива в цикле и характеризуются линейной вычислительной сложностью O(n). В частности, для получения индекса самого левого дочернего узла по индексу родителя, следует перебрать все ячейки индексов родительских узлов в поиске ближайшего, чей индекс узла-родителю равен интересующему:
intTreeGetLeftmostChildIndex( constTree & _tree, int_nodeIndex )
{
// Проверяем корректность индекса
assert( _nodeIndex < _tree.m_nNodes );
// Ищем первый узел, индекс родителя которого равен искомому
for( inti = _nodeIndex + 1; i < _tree.m_nNodes; i++ )
if( _tree.m_pParentIndices[ i ] == _nodeIndex )
// Конкретный узел найден
returni;
// Дочерних узлов не найдено
return-1;
}
Аналогичным образом реализуется поиск ближайшего правого братского узла:
intTreeGetRightSiblingIndex ( constTree & _tree, int_nodeIndex )
{
// Проверяем корректность индекса
assert( _nodeIndex < _tree.m_nNodes );
// Получаем индекс узла-родителя
intparentIndex = TreeGetParentIndex( _tree, _nodeIndex );
// Начинаем поиск правого братского узла сразу после своего узла.
// Братский узел будет иметь такой же индекс узла-родителя, как и данный узел.
for( inti = _nodeIndex + 1; i < _tree.m_nNodes; i++ )
if( _tree.m_pParentIndices[ i ] == parentIndex )
// Конкретный узел найден
returni;
// Братских узлов не найдено
return-1;
}
Наконец, следующим образом выглядят функции обхода:
// Прямой обход дерева, начиная с конкретного узла
voidTreeDirectWalk ( constTree & _tree, int_nodeIndex, TreeNodeVisitFunction _f )
{
// Посещаем начальный узел
( *_f )( _tree, _nodeIndex );
// Рекурсивно вызываем обход для каждого дочернего узла
intchildIndex = TreeGetLeftmostChildIndex( _tree, _nodeIndex );
while( childIndex != -1 )
{
TreeDirectWalk( _tree, childIndex, _f );
childIndex = TreeGetRightSiblingIndex( _tree, childIndex );
}
}
// Обратный обход дерева, начиная с конкретного узла
voidTreeReverseWalk ( constTree & _tree, int_nodeIndex, TreeNodeVisitFunction _f )
{
// Рекурсивно вызываем обход для каждого дочернего узла
intchildIndex = TreeGetLeftmostChildIndex( _tree, _nodeIndex );
while( childIndex != -1 )
{
TreeReverseWalk( _tree, childIndex, _f );
childIndex = TreeGetRightSiblingIndex( _tree, childIndex );
}
// В конце посещаем узел-родитель
( *_f )( _tree, _nodeIndex );
}
// Симметричный обход дерева, начиная с конкретного узла
voidTreeSymmetricWalk ( constTree & _tree, int_nodeIndex, TreeNodeVisitFunction _f )
{
// Рекурсивно посещаем самый левый дочерний узел, если такой имеется
intchildIndex = TreeGetLeftmostChildIndex( _tree, _nodeIndex );
if( childIndex != -1 )
TreeSymmetricWalk( _tree, childIndex, _f );
// Посещаем узел-родитель
( *_f )( _tree, _nodeIndex );
// Без дочерних узлов дальше двигаться не куда
if( childIndex == -1 )
return;
// Рекурсивно посещаем каждый следующий дочерний узел
while( true)
{
childIndex = TreeGetRightSiblingIndex( _tree, childIndex );
if( childIndex == -1 )
break;
TreeSymmetricWalk( _tree, childIndex, _f );
}
}
// Прямой обход дерева, начиная с корня
voidTreeDirectWalk ( constTree & _tree, TreeNodeVisitFunction _f )
{
TreeDirectWalk( _tree, TreeGetRootIndex( _tree ), _f );
}
// Обратный обход дерева, начиная с корня
voidTreeReverseWalk ( constTree & _tree, TreeNodeVisitFunction _f )
{
TreeReverseWalk( _tree, TreeGetRootIndex( _tree ), _f );
}
// Симметричный обход дерева, начиная с корня
voidTreeSymmetricWalk ( constTree & _tree, TreeNodeVisitFunction _f )
{
TreeSymmetricWalk( _tree, TreeGetRootIndex( _tree ), _f );
}
Отметим, что функции обхода не используют внутреннее представление дерева, полностью удовлетворяясь доступными операциями. Это означает, что для повторного использования в других реализациях деревьев, можно вынести этот набор функций в отдельный CPP-файл.
Дата добавления: 2016-01-29; просмотров: 1065;
