Динамическая структура с указателями

Вышеописанные структуры данных плохо подходят для реализации деревьев, о которых заранее не известно количество узлов. В ситуации, когда структура дерева изменяется динамически, следует воспользоваться более гибким решением, напоминающим связный список.

Структура узла, представленная ниже, предполагает хранение в нем некоторого значения-метки, а также 3 переменных-указателей: на родительский узел, на самый левый дочерний узел и на соседний братский узел справа:

structTreeNode

{

TreeNodeLabel m_label;

TreeNode* m_pParent;

TreeNode* m_pLeftMostChild;

TreeNode* m_pRightSibling;

};

Собственно, структура-дерево сводится к хранению указателя на корневой узел:

structTree

{

TreeNode * m_pRoot;

};

Создается дерево такого типа одновременно с корневым узлом:

TreeNode * TreeCreateNode ( TreeNodeLabel _label )

{

TreeNode * pNode = newTreeNode;

pNode->m_label = _label;

pNode->m_pParent = pNode->m_pLeftMostChild = pNode->m_pRightSibling = nullptr;

returnpNode;

}

Tree * TreeCreate ( TreeNodeLabel_rootLabel )

{

Tree * pTree = newTree;

pTree->m_pRoot = TreeCreateNode ( _rootLabel );

returnpTree;

};

Чтобы добавить новый дочерний узел к конкретному узлу дерева, необходимо лишь настроить соответствующим образом переменные-указатели:

TreeNode * TreeInsertNodeChild ( TreeNode * _pNode, char_newLabel )

{

// Создаем новый узел

TreeNode * pNewNode = TreeCreateNode( _newLabel );

// Родительским узлом будет указанный свыше узел

pNewNode->m_pParent = _pNode;

// Присоединяем новый узел к родительскому.

// Это первый дочерний узел у данного родителя?

if( ! _pNode->m_pLeftMostChild )

// Да, пусть новый узел будет его самым левым дочерним

_pNode->m_pLeftMostChild = pNewNode;

Else

{

// Находим самый правый дочерний узел данного родителя

TreeNode * pTemp = _pNode->m_pLeftMostChild;

while( pTemp->m_pRightSibling )

pTemp = pTemp->m_pRightSibling;

// Новый узел будет прикреплен к самому правому братскому узлу

pTemp->m_pRightSibling = pNewNode;

}

returnpNewNode;

};

Логика уничтожения узлов дерева при освобождении памяти реализуется рекурсивно:

voidTreeNodeDestroy ( TreeNode * _pNode )

{

// Сначала уничтожаем все зарегистрированные дочерние узлы слева-направо

TreeNode * pCurrent = _pNode->m_pLeftMostChild;

while( pCurrent )

{

TreeNode * pNext = pCurrent->m_pRightSibling;

TreeNodeDestroy( pCurrent ); // рекурсивный спуск к листьям дерева

pCurrent = pNext;

}

delete_pNode;

}

voidTreeDestroy ( Tree * _pTree )

{

TreeNodeDestroy( _pTree->m_pRoot );

delete_pTree;

}

Вместо номеров позиций во всех запросах следует возвращать указатели на узлы дерева. Очевидно, что все соответствующие операции, такие как ROOT, PARENT, LEFTMOST_CHILD, RIGHT_SIBLING, LABEL - при такой организации данных будут иметь константную вычислительную сложность, поскольку реализация может напрямую задействовать указатели-связи в узлах:

TreeNode * TreeGetRootNode ( Tree * _pTree )

{

return_pTree->m_pRoot;

}

TreeNodeLabelTreeGetLabel ( TreeNode * _pNode )

{

return_pNode->m_label;

}

TreeNode * TreeGetParent ( TreeNode * _pNode )

{

return_pNode->m_pParent;

}

TreeNode * TreeGetLeftMostChild ( TreeNode * _pNode )

{

return_pNode->m_pLeftMostChild;

}

TreeNode * TreeGetRightSibling ( TreeNode * _pNode )

{

return_pNode->m_pRightSibling;

}

Несколько иначе выглядит обход деревьев такого рода. Во-первых, видоизменяется форма типа для функции обратного вызова, теперь принимающая ссылку на узел вместо номера узла:

typedef void( * TreeNodeVisitFunction ) ( constTreeNode & _node );

Во-вторых, несколько преображается способ навигации между узлами дерева:

// Прямой обход дерева, начиная с указанного узла

voidTreeDirectWalk ( constTreeNode * _pNode,
TreeNodeVisitFunction _f )

{

// Посещаем узел-родитель

( * _f )( * _pNode );

// Посещаем дочерние узлы рекурсивно

TreeNode * pChild = _pNode->m_pLeftMostChild;

while( pChild )

{

TreeDirectWalk( pChild, _f );

pChild = pChild->m_pRightSibling;

}

}

// Обратный обход дерева, начиная с указанного узла

voidTreeReverseWalk ( constTreeNode * _pNode,

TreeNodeVisitFunction _f )

{

// Посещаем дочерние узлы рекурсивно

TreeNode * pChild = _pNode->m_pLeftMostChild;

while( pChild )

{

TreeReverseWalk( pChild, _f );

pChild = pChild->m_pRightSibling;

}

// В конце посещаем узел-родитель

( * _f )( * _pNode );

}

// Симметричный обход дерева, начиная с указанного узла

voidTreeSymmetricWalk ( constTreeNode * _pNode,

TreeNodeVisitFunction _f )

{

// Посещаем рекурсивно левый дочерний узел, если такой имеется

if( _pNode->m_pLeftMostChild )

TreeSymmetricWalk( _pNode->m_pLeftMostChild, _f );

// Посещаем узел-родитель

( * _f )( * _pNode );

// Если дочерних узлов нет, обход закончен

TreeNode * pChild = _pNode->m_pLeftMostChild;

if( ! pChild )

return;

// Посещаем рекурсивно все оставшиеся дочерние узлі

while( true)

{

pChild = pChild->m_pRightSibling;

if( ! pChild )

break;

TreeSymmetricWalk( pChild, _f );

}

}

// Прямой обход дерева, начиная с корня

voidTreeDirectWalk ( constTree & _t, TreeNodeVisitFunction _f )

{

TreeDirectWalk( _t.m_pRoot, _f );

}

// Обратный обход дерева, начиная с корня

voidTreeReverseWalk ( constTree & _t, TreeNodeVisitFunction _f )

{

TreeReverseWalk( _t.m_pRoot, _f );

}

// Симметричный обход дерева, начиная с корня

voidTreeSymmetricWalk ( constTree & _t, TreeNodeVisitFunction _f )

{

TreeSymmetricWalk( _t.m_pRoot, _f );

}

Ниже приведена тестовая программа, формирующая рассматриваемое дерево-пример при помощи динамического дерева:

// Функция посещения узла при обходе

voidPrintNodeLabel ( constTreeNode & _node )

{

std::cout << _node.m_label << ' ';

}

intmain ()

{

// Создание дерева с меткой корня ‘A’

Tree * pTree = TreeCreate( 'A' );

// Добавляем дочерние узлы к корню

TreeNode * pNodeB = TreeInsertChild( pTree->m_pRoot, 'B' );

TreeNode * pNodeC = TreeInsertChild( pTree->m_pRoot, 'C' );

TreeInsertChild( pTree->m_pRoot, 'D' );

// Добавляем дочерние узлы к узлу ‘B’

TreeInsertChild( pNodeB, 'E' );

TreeInsertChild( pNodeB, 'F' );

// Добавляем дочерние узлы к узлу ‘C’

TreeInsertChild( pNodeC, 'G' );

// Обход дерева 3 способами с распечаткой значений:

// 1) Прямой

TreeDirectWalk( * pTree, & PrintNodeLabel );

std::cout << std::endl;

// 2) Обратный

TreeReverseWalk( * pTree, & PrintNodeLabel );

std::cout << std::endl;

// 3) Симметричный

TreeSymmetricWalk( * pTree, & PrintNodeLabel );

std::cout << std::endl;

// Уничтожение дерева

TreeDestroy( pTree );

}

В результате ее выполнения в динамической памяти формируется структура объектов, в существенной степени напоминающая оригинальный пример из описания понятия деревьев:

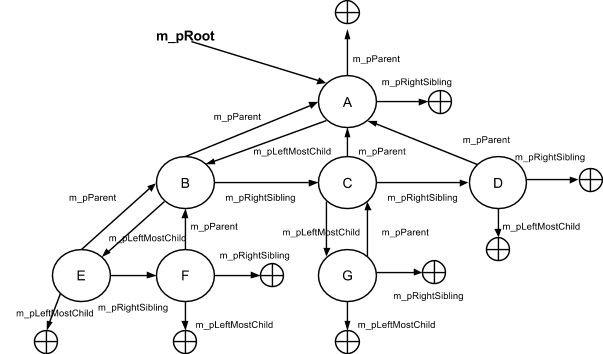
Минусом такого способа организации дерева является существенно больший расход оперативной памяти. Каждый узел здесь выделяется динамически отдельно, что приводит к большому количеству операций выделения и освобождения небольшого блока. Общее количество необходимой памяти возрастает, так как каждое выделение имеет собственные накладные служебные расходы, мало зависящие от размера фактически выделенной “полезной” памяти.

Бинарные деревья

Для бинарного дерева, т.е. дерева, в котором имеется не более двух дочерних узлов у каждого узла-родителя, представляется возможным существенно упростить рассмотренные выше структуры данных. В частности, структура дерева с фиксированным количеством узлов упрощается до следующей:

structTree

{

structNodeData

{

TreeNodeLabel m_label;

intm_parentIndex;

intm_leftChildIndex;

intm_rightChildIndex;

};

intm_nNodes;

NodeData * m_pNodes;

};

Используя ограничение на количество дочерних узлов, представляется возможным полностью избавиться от связных списков при хранении данных о дочерних узлах в узле-родителе. Кроме того, удается улучшить вычислительную сложность “проблемных операций” - PARENT и RIGHT_SIBLING - до константной:

intTreeGetParentIndex ( Tree * _pTree, int_nodeIndex )

{

Tree::NodeData * pNodeData = _pTree->m_pNodes + _nodeIndex;

returnpNodeData->m_parentIndex;

}

intTreeGetRightSiblingIndex ( Tree * _pTree, int_nodeIndex )

{

Tree::NodeData * pNodeData = _pTree->m_pNodes + _nodeIndex;

Tree::NodeData * pParentNodeData = _pTree->m_pNodes + pNodeData->m_parentIndex;

if( pParentNodeData->m_leftChildIndex == _nodeIndex )

returnpParentNodeData->m_rightChildIndex;

Else

return-1;

}

Динамическая структура на основе указателей также может быть упрощена до хранения непосредственной связи с левым и правыми поддеревьями:

structTreeNode

{

TreeNodelabel m_label;

TreeNode * m_pParent;

TreeNode * m_pLeftChild;

TreeNode * m_pRightChild;

};

Упрощение не влияет на требуемый объем памяти или вычислительную сложность операций, однако заметно упрощает рекурсивную обработку. Например, в процедуре уничтожения дерева удается избавиться от цикла и упростить задачу до элементарных рекурсивных вызовов:

voidTreeNodeDestroy( TreeNode * _pNode )

{

if( _pNode->m_pLeftChild )

NodeDestroy( _pNode->m_pLeftChild );

if( _pNode->m_pRightChild )

NodeDestroy( _pNode->m_pRightChild );

delete_pNode;

}

Выводы

В данной лекции был рассмотрен абстрактный тип данных “Дерево”, имеющий широкое распространение в программировании при решении различных практических задач. Фактически, деревья могут использоваться для моделирования иерархической структуры любой сложности. Были предложены различные альтернативные структуры данных, реализующие операции с деревьями, с приведением оценок вычислительной сложности.