Характеристическое свойство BST

На основе бинарных деревьев представляется возможным эффективно реализовать АТД “Отображение” и “Множество”, при условии, что ключи могут быть упорядочены по оператору <. Этому условию удовлетворяют большинство используемых на практике типов данных ключей. Для чисел используется естественный смысл операции меньше, для строк - алфавитный порядок, для перечисляемых типов - порядок объявления меток. При необходимости, можно определить смысл операции < для массивов (по аналогии со строками) и структур (исходя из логики понятия).

Предположим, имеется неупорядоченный набор уникальных чисел:

5 2 7 3 9 0 1 4 6 8

Добавляя на каждом шаге числа при последовательном переборе, сформируем из данного набора бинарное дерево с узлами, метками которого являются эти числа, таким образом, что всегда будет соблюдаться следующее характеристическое свойство:

• любой ключ, находящийся в левом поддереве, меньше ключа в узле-родителе
• любой ключ, находящийся в правом поддереве, больше ключа в узле-родителе.

Если во входном наборе попадется повторяющееся число, его следует либо проигнорировать, либо следует сигнализировать внешней среде об ошибке.

Ниже в графической форме приведена пошаговая процедура добавления рассматриваемой последовательности чисел в дерево. Первое число 5 попадает в корневой узел:

Число 2 меньше числа 5, поэтому оно будет размещено в левом поддереве:

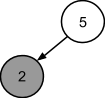
Число 7 больше числа 5, в связи с чем его следует поместить в правом поддереве:

В дальнейшем процедура будет выполняться рекурсивно. Следует сравнивать очередное входное число с текущим узлом-родителем, начиная от корня, и, если вставляемое в дерево новое число-ключ меньше числа в узле-родителе, новый узел должен вставляться в левое поддерево, а если больше - в правое. Число 3 меньше 5, значит следует двигаться по левому поддереву. Число 3 больше 2, соответственно, это число должно стать правым поддеревом для узла с числом 2:

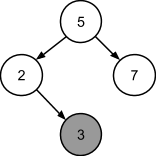
Число 9 больше числа 5 и больше числа 7, его место в правом поддереве узла с числом 7:

Число 0 меньше числа 5 и меньше числа 2, его поместим в левом поддереве узла с числом 2:

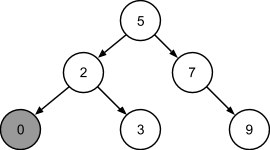
Число 1 меньше числа 5, меньше числа 2, однако больше числа 0. Значит, у узла с числом 0 должно появиться правое поддерево:

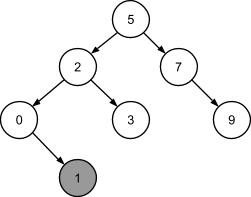
Число 4 меньше числа 5, больше числа 2 и больше числа 3, соответственно такое число будет размещено в правом поддереве узла с числом 3:

Число 6 больше числа 5, но меньше числа 7. Узел с числом 7 получит левое поддерево:

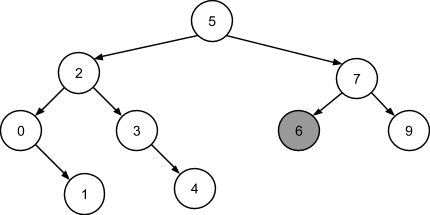
Число 8 больше 5, больше 7, но меньше 9, следовательно узел 9 получит левое поддерево:

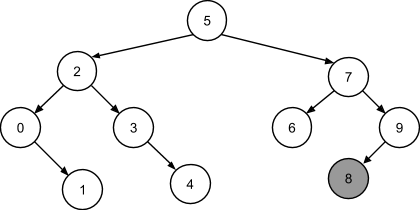
Бинарные деревья, ключи в узлах которых упорядочены в соответствии с продемонстрированным выше характеристическим свойством, называются деревьями бинарного поиска (BST).

Реализация BST

Наиболее удобный способ реализации BST - динамическая структура для деревьев, рассмотренная в предыдущей лекции о деревьях общего назначения. Структура должна сопровождаться типичными операциями АТД “множество” для поиска, вставки и удаления ключей.

bstree.hpp:

#ifndef _BSTREE_HPP_

#define _BSTREE_HPP_

////////////////////////////////////////////////////////////////////////

structBSTree

{

structNode

{

intm_key;

Node * m_pParent;

Node * m_pLeft;

Node * m_pRight;

};

Node * m_pRoot;

};

///////////////////////////////////////////////////////////////////////

// Создание объекта-дерева

BSTree * BSTreeCreate ();

// Уничтожение объекта-дерева

voidBSTreeDestroy ( BSTree * _pTree );

// Вставка указанного ключа в дерево

voidBSTreeInsertKey ( BSTree & _tree, int_key );

// Проверка наличия указанного ключа в дереве

boolBSTreeHasKey ( constBSTree & _tree, int_key );

// Удаление указанного ключа из дерева

voidBSTreeDeleteKey ( BSTree & _tree, int_key );

///////////////////////////////////////////////////////////////////////

#endif // _BSTREE_HPP_

Функции создания и уничтожения реализуются аналогично обычным бинарным деревьям:

bstree.cpp

#include "bstree.hpp"

#include <cassert>

// Создание объекта-дерева

BSTree * BSTreeCreate ()

{

BSTree * pTree = newBSTree;

pTree->m_pRoot = nullptr;

returnpTree;

}

// Вспомогательная рекурсивная функция для удаления поддерева

voidBSTreeDestroy ( BSTree::Node * _pNode )

{

if( ! _pNode )

return;

BSTreeDestroy( _pNode->m_pLeft );

BSTreeDestroy( _pNode->m_pRight );

delete_pNode;

}

// Уничтожение объекта-дерева

voidBSTreeDestroy ( BSTree * _pTree )

{

BSTreeDestroy( _pTree->m_pRoot );

}

Ниже показан пример реализации описанного алгоритма вставки в BST:

// Вспомогательная функция создания нового узла с указанным ключом

BSTree::Node * BSTreeCreateNode ( int_key )

{

// Создаем объект-узел

BSTree::Node * pNewNode = newBSTree::Node;

// Запоминаем в узле значение ключа

pNewNode->m_key = _key;

// Обнуляем все связи узла с соседями

pNewNode->m_pLeft = pNewNode->m_pRight = pNewNode->m_pParent = nullptr;

// Возвращаем созданный узел

returnpNewNode;

}

// Вставка указанного ключа в дерево

voidBSTreeInsertKey ( BSTree & _tree, int_key )

{

// Особый случай - вставка первого ключа в пустое дерево

BSTree::Node * pCurrent = _tree.m_pRoot;

if( ! pCurrent )

{

_tree.m_pRoot = BSTreeCreateNode( _key );

return;

}

// Ищем позицию в дереве для вставки нового ключа, начиная с корня

while( pCurrent )

{

// При равенстве ключей, игнорируем вставку

if( pCurrent->m_key == _key )

return;

// Когда новый ключ меньше ключа в текущем узле, движемся в левую сторону

else if( _key < pCurrent->m_key )

{

// Если левое поддерево уже есть, применяем алгоритм к его корню

if( pCurrent->m_pLeft )

pCurrent = pCurrent->m_pLeft;

// Левого поддерева нет, новый узел становится левым поддеревом

Else

{

BSTree::Node * pNewNode = BSTreeCreateNode( _key );

pNewNode->m_pParent = pCurrent;

pCurrent->m_pLeft = pNewNode;

return;

}

}

// Когда новый ключ больше ключа в текущем узле, движемся в правую сторону

Else

{

// Если правое поддерево уже есть, применяем алгоритм к его корню

if( pCurrent->m_pRight )

pCurrent = pCurrent->m_pRight;

Else

{

// Правого поддерева нет, новый узел становится правым поддеревом

BSTree::Node * pNewNode = BSTreeCreateNode( _key );

pNewNode->m_pParent = pCurrent;

pCurrent->m_pRight = pNewNode;

return;

}

}

}

}

Теперь, если требуется выяснить имеется ли интересующий ключ в дереве, следует применить подобный рекурсивный алгоритм:

1. Начать анализ с узла-корня и назначить его текущим.
2. Сравнить искомый ключ с ключом в текущем узле:

1. Если искомый ключ меньше ключа в узле, следует рекурсивно выполнить шаг 2 на левом поддереве, либо завершить поиск, если левого поддерева нет.
2. Если искомый ключ больше ключа в узле, следует рекурсивно выполнить шаг 2 на правом поддереве, либо завершить поиск, если правого поддерева нет.
3. Если ключи равны, значит искомый узел найден.

Допустим, требуется узнать имеется ли число 4 в дереве. Выполняем описанный выше рекурсивный алгоритм и приходим от корня к искомому узлу. Ниже графически показан процесс обхода бинарного дерева поиска, при помощи цвета заливки выделен пройденный от корня путь:

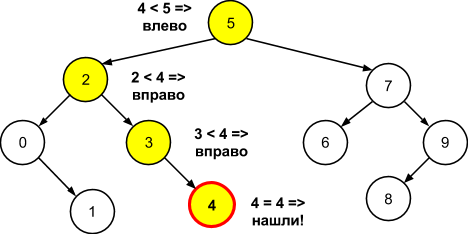
Ниже приведена реализация данного алгоритма поиска:

// Вспомогательная функция поиска узла с интересующим ключом в дереве

BSTree::Node * BSTreeFindKeyNode ( constBSTree & _tree, int_key )

{

// Начинаем поиск с корневого узла

BSTree::Node * pCurrent = _tree.m_pRoot;

while( pCurrent )

{

// Если искомый ключ равен ключу из текущего узла, нужный узел найден!

if( _key == pCurrent->m_key )

returnpCurrent;

// Если искомый ключ меньше ключа текущего узла, движемся по левому поддереву

else if( _key < pCurrent->m_key )

pCurrent = pCurrent->m_pLeft;

// Если искомый ключ больше ключа текущего узла, движемся по правому поддереву

Else

pCurrent = pCurrent->m_pRight;

}

// Узел с таким ключом не найден

return nullptr;

}

// Проверка наличия указанного ключа в дереве

boolBSTreeHasKey ( constBSTree & _tree, int_key )

{

// Ключ принадлежит множеству, если имеется узел с таким же ключом

returnBSTreeFindKeyNode( _tree, _key ) != nullptr;

}

Фактически, алгоритмы поиска, вставки, удаления по ключу в бинарном дереве поиска во многом похожи. Следует найти либо сам узел в дереве, рекурсивно спускаясь, выбирая направление по результатам сравнения ключей, либо тем же способом найти место его потенциального расположения при вставке.

Вычислительная сложность таких алгоритмов пропорционально зависит от длины пути в дереве, т.е. от высоты дерева. В идеальном случае, когда высота листьев приблизительно одинаковая, количество рассматриваемых в процессе поиска узлов имеет логарифмическую зависимость от общего числа узлов в дереве O(log₂ N). Это менее благоприятная вычислительная сложность по сравнению с хэш-таблицами O(1), однако существенно лучшая по сравнению с линейным поиском в массивах или списках O(N).