Несбалансированные BST и вращение

Бинарное дерево поиска, у которого для любого узла-родителя количество дочерних узлов в левом и правом поддереве приблизительно равны, называется сбалансированным. Обратный случай, когда имеется существенный перевес у одного из двух поддеревьев, образует несбалансированное дерево. Вычислительная сложность процедуры поиска имеет логарифмическую сложность лишь для сбалансированных деревьев. Если баланс поддеревьев нарушен, сложность процедуры поиска в худшем случае вырождается до линейной.

Худшим случаем для работы BST является ввод уже упорядоченной последовательности, например:

0 1 2 3 4 5 6 7 8 9

Описанный выше алгоритм вставки для такой последовательности сформирует крайне неудачное с точки зрения поиска бинарное дерево - абсолютно несбалансированное BST, несмотря на соблюдение характеристического свойства:

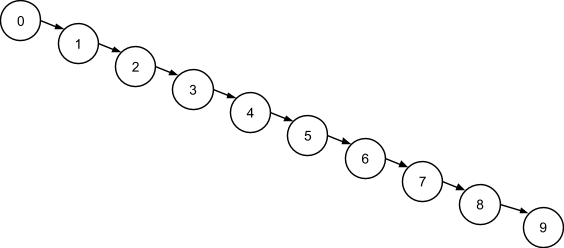
Фактически, такое дерево превращается в односвязный список с линейной вычислительной сложностью поиска. Очевидно, в базовой форме деревья бинарного поиска не могут успешно обрабатывать уже упорядоченные последовательности.

Существует ряд алгоритмов автоматической балансировки деревьев, дополняющих базовую идею BST. Большинство из них основано на применении операции вращения. Суть вращения состоит в повороте одной из связей (оси вращения) в дереве по часовой (правое вращение) или против часовой стрелки (левое вращение) в зависимости от текущей потребности алгоритма. Вращение в конкретной области дерева помогает уменьшить возможный дисбаланс между высотами левого и правого поддеревьев. В какой именно момент времени и какую связь следует повернуть зависит от используемого алгоритма. Ниже рассмотрены сами операции вращения.

Предположим имеется следующее дерево, и тот или иной алгоритм принимает решение осуществить правое вращение связи между узлами-полюсами B и D. Выбранные узлы можно поменять местами, при условии, что характеристическое свойство BST не будет нарушено:

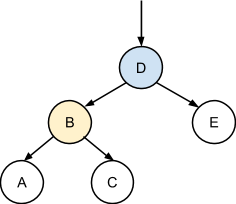
В начале узлы-полюса B и D вокруг оси вращения следует расцепить:

Затем, правое поддерево C левого полюса B следует перекрепить к освободившемуся месту в левом поддереве правого полюса D:

Затем можно перекрепить левый полюс B с родительским узлом правого полюса D, поскольку после расцепления полюсов эта связь является свободной. В частном случае, родительской связи может не быть, в таком случае D является корневым узлом дерева, а новым корнем станет B:

Наконец, можно прикрепить правый полюс D к левому полюсу B со свободной правой стороны, тем самым завершая операцию вращения без нарушения характеристического свойства BST:

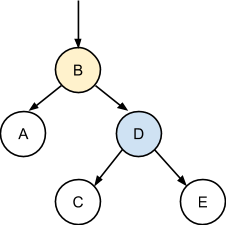
Любого из соседних узлов - A, C, E, а также родительской связи в дереве может не быть, что не изменит сути рассмотренного алгоритма, лишь упростив его шаги.

Левое вращение реализуется аналогично и симметрично, фактически, следует выполнить шаги алгоритма правого вращения в обратном порядке.

Следует отметить, что операция вращения является локальной относительно выбранной оси. Модифицируются лишь связи узлов-полюсов B и D, а также родительская связь узла-поддерева C, ключ которого находится между ключами во вращаемых узлах-полюсах. Состояние других узлов не модифицируется, а значит данная операция обладает высоким быстродействием.

Ниже приведен код функций, реализующий левое и правое вращение:

voidBSTreeLeftRotate ( BSTree & _tree, BSTree::Node * _l )

{

// l - левый полюс вращения, r - правый полюс вращения.

// Ось вращения - связь между l и r

BSTree::Node* r = _l->m_pRight;

// Если правого полюса нет, вращать нечем

if( ! r )

return;

// Перекрепляем промежуточный узел к правой ветви левого полюса

_l->m_pRight = r->m_pLeft;

if( _l->m_pRight )

_l->m_pRight->m_pParent = _l;

// Перекрепляем родительскую связь с левого полюса на правый

// Случай 1: левый полюс - корень, правый полюс становится новым корнем

// Случай 2: левый полюс является левым ребенком своего родителя

// Случай 3: левый полюс является правым ребенком своего родителя

r->m_pParent = _l->m_pParent;

if( ! r->m_pParent )

_tree.m_pRoot = r;

else if( _l == _l->m_pParent->m_pLeft )

_l->m_pParent->m_pLeft = r;

else if( _l == _l->m_pParent->m_pRight )

_l->m_pParent->m_pRight = r;

Else

// Иная ситуация невозможна

assert( 0 );

// Воссоздаем ось между полюсами в противоположном направлении

r->m_pLeft = _l;

_l->m_pParent = r;

}

voidBSTreeRightRotate ( BSTree & _tree, BSTree::Node * _r )

{

// l - левый полюс вращения, r - правый полюс вращения.

// Ось вращения - связь между l и r

BSTree::Node* l = _r->m_pLeft;

// Если левого полюса нет, вращать нечем

if( ! l )

return;

// Перекрепляем промежуточный узел к левой ветви правого полюса

_r->m_pLeft = l->m_pRight;

if( _r->m_pLeft )

_r->m_pLeft->m_pParent = _r;

// Перекрепляем родительскую связь с правого полюса на левый

// Случай 1: правый полюс - корень, левый полюс становится новым корнем

// Случай 2: правый полюс является левым ребенком своего родителя

// Случай 3: правый полюс является правым ребенком своего родителя

l->m_pParent = _r->m_pParent;

if( ! l->m_pParent )

_tree.m_pRoot = l;

else if( _r == _r->m_pParent->m_pLeft )

_r->m_pParent->m_pLeft = l;

else if( _r == _r->m_pParent->m_pRight )

_r->m_pParent->m_pRight = l;

Else

// Иная ситуация невозможна

assert( 0 );

// Воссоздаем ось между полюсами в противоположном направлении

l->m_pRight = _r;

_r->m_pParent = l;

}