Важно! По умолчанию новый узел всегда красный!

pNewNode->m_color = RBTree::Node::RED;

pNewNode->m_pLeft = pNewNode->m_pRight = pNewNode->m_pParent = nullptr;

returnpNewNode;

}

// Базовая функция вставки, аналогично классической вставке в BST.

// Дополнительно возвращает указатель на новый узел

RBTree::Node * RBTreeInsertBase ( RBTree & _tree, int_key )

{

// Особый случай - вставка первого ключа в пустое дерево

RBTree::Node * pCurrent = _tree.m_pRoot;

if( ! pCurrent )

{

_tree.m_pRoot = RBTreeCreateNode( _key );

return_tree.m_pRoot;

}

// Ищем позицию в дереве для вставки нового ключа, начиная с корня

while( pCurrent )

{

// При равенстве ключей, игнорируем вставку

if( pCurrent->m_key == _key )

return nullptr;

// Когда новый ключ меньше ключа в текущем узле, движемся в левую сторону

else if( _key < pCurrent->m_key )

{

// Если левое поддерево уже есть, применяем алгоритм к его корню

if( pCurrent->m_pLeft )

pCurrent = pCurrent->m_pLeft;

// Левого поддерева нет, новый узел становится левым поддеревом

Else

{

RBTree::Node * pNewNode = RBTreeCreateNode( _key );

pNewNode->m_pParent = pCurrent;

pCurrent->m_pLeft = pNewNode;

returnpNewNode;

}

}

// Когда новый ключ больше ключа в текущем узле, движемся в правую сторону

Else

{

// Если правое поддерево уже есть, применяем алгоритм к его корню

if( pCurrent->m_pRight )

pCurrent = pCurrent->m_pRight;

// Правого поддерева нет, новый узел становится правым поддеревом

Else

{

RBTree::Node * pNewNode = RBTreeCreateNode( _key );

pNewNode->m_pParent = pCurrent;

pCurrent->m_pRight = pNewNode;

returnpNewNode;

}

}

}

// Дойти до данного кода при корректной реализации невозможно!

assert( 0 );

return nullptr;

}

// Функция извлечения цвета узла. Если узла нет - представим, что он черный

RBTree::Node::Color RBTreeColorOf ( const RBTree::Node * _pNode )

{

return( _pNode ) ? _pNode->m_color : RBTree::Node::BLACK;

}

// Основная процедура вставки нового ключа в красно-черное дерево

voidRBTreeInsertKey ( RBTree & _tree, int_key )

{

// Вызываем базовую процедуру вставки ключа в BST

RBTree::Node * x = RBTreeInsertBase( _tree, _key );

// Если узел не был вставлен, корректировать нечего

if( ! x )

return;

// Пытаемся обнаружить пару родитель-дочерний узел красного цвета

RBTree::Node * p;

while( x && ( p = x->m_pParent ) && RBTreeColorOf( p ) == RBTree::Node::RED )

{

// Для коррекций иерархии необходим узел-дед

RBTree::Node* pp = p->m_pParent;

// Является ли узел-родитель левым ребенком узла-деда?

if( p == pp->m_pLeft )

{

// Имеется ли красный узел-дядя? (случаи 1 и 2)

RBTree::Node* y = pp->m_pRight;

if( RBTreeColorOf( y ) == RBTree::Node::RED )

{

// Делаем родителя и дядю черными, а дедушку - красным

p->m_color = RBTree::Node::BLACK;

y->m_color = RBTree::Node::BLACK;

pp->m_color = RBTree::Node::RED;

// Продолжаем анализ с уровня дедушки

x = pp;

}

Else

{

// Является ли новый узел правым поддеревом родителя? (случай 4)

if( x == p->m_pRight )

{

// Делаем левое вращение, сводим к случаю 3

x = p;

RBTreeLeftRotate( _tree, x );

}

p = x->m_pParent;

pp = p->m_pParent;

// Случай 3 - делаем родителя черным, дедушку красным,

// затем вращаем ось между родителем и дедушкой вправо

p->m_color = RBTree::Node::BLACK;

if( pp )

{

pp->m_color = RBTree::Node::RED;

RBTreeRightRotate( _tree, pp );

}

}

}

// Узел-родитель является правым ребенком узла-деда

else

{

// Имеется ли красный узел-дядя? (случаи 1 и 2)

RBTree::Node* y = pp->m_pLeft;

if( RBTreeColorOf( y ) == RBTree::Node::RED )

{

// Делаем родителя и дядю черными, а дедушку - красным

p->m_color = RBTree::Node::BLACK;

y->m_color = RBTree::Node::BLACK;

pp->m_color = RBTree::Node::RED;

// Продолжаем анализ с уровня дедушки

x = pp;

}

Else

{

// Является ли новый узел левым поддеревом родителя? (случай 4)

if( x == p->m_pLeft )

{

// Делаем правое вращение, сводим к случаю 3

x = p;

RBTreeRightRotate( _tree, x );

}

p = x->m_pParent;

pp = p->m_pParent;

// Случай 3 - делаем родителя черным, дедушку красным,

// затем вращаем ось между родителем и дедушкой влево

p->m_color = RBTree::Node::BLACK;

if ( pp )

{

pp->m_color = RBTree::Node::RED;

RBTreeLeftRotate( _tree, pp );

}

}

}-

}

// Решаем проблему со цветом корневого узла

_tree.m_pRoot->m_color = RBTree::Node::BLACK;

}

Попробуем применить описанный и реализованный алгоритм к отсортированной по возрастанию последовательности от 0 до 9, которая “повергла в уныние” классический вариант бинарного дерева поиска. В начале вставляется первый ключ 0, который становится черным корнем:

Узел 1 прикрепляется справа базовым алгоритмом, и дерево при этом не нуждается в коррекциях:

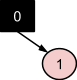
Узел 2 прикрепляется базовым алгоритмом справа, при этом нарушая правило красно-черного дерева о черных дочерних узлах красного родительского узла. Это случай 3 из рассмотренных коррекций, поскольку узла-дяди в дереве нет, а вращать узлы 1 и 2 между собой не требуется. На первом шаге меняем цвета узлов 0 (дед) и узлов 1 (родитель), а затем осуществляем левое вращение по оси между 0 и 1:

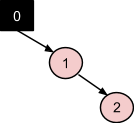
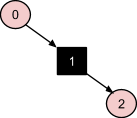
Узел 3 также формирует пару красных узлов родитель-потомок, однако эта ситуация относится к случаю 1 из описанных коррекций, поскольку узел 0 в данный момент является красным узлом-дядей по отношению к 3. Соответственно, следует перекрасить деда, дядю и родителя в противоположные цвета. В конце, цвет деда обращается в черный еще раз, как корня дерева:

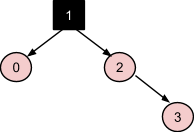
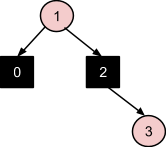
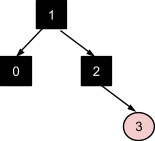
Узел 4 повторяет ситуацию с узлом 2 (коррекция №3), на этом дерево стабилизируется:

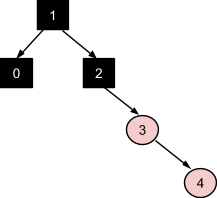
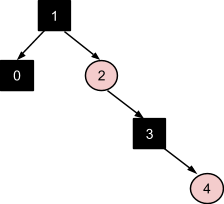
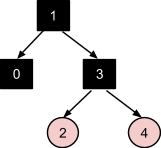
Обработка вставки узла 5 похожа на обработку вставки узла 3:

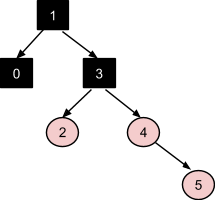
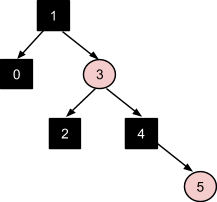
Обработка вставки узла 6 похожа на обработку вставки узлов 2 и 4. В результате применения коррекции №3, получаем стабильное дерево:

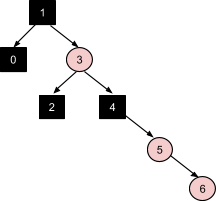
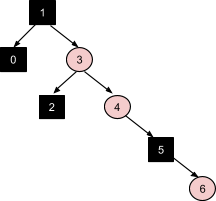
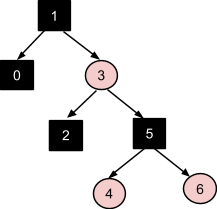
Вставка узла 7 активизирует большее число преобразований в дереве. В начале применяется коррекция №1, т.к. имеется узел-дядя 4 красного цвета. Это образует проблему с красными узлами 3 и 5. Новый случай активизирует коррекцию №3 при узле-деде 1, который является корневым в данный момент. Это преобразование приводит к получению нового корня 3:

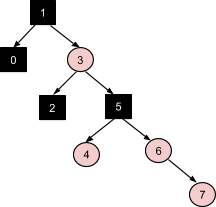
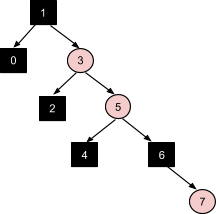
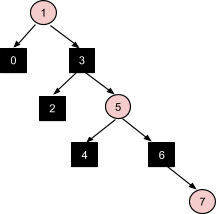
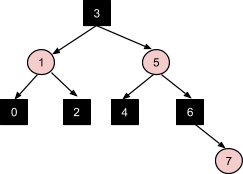
Вставка узла 8 - прямое соответствие коррекции №3, без дальнейших распространений:

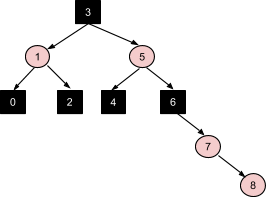
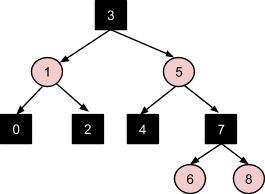
Наконец вставка числа 9 - это последовательное применение коррекции №1, затем №3, а затем перекрашивание корня в черный цвет:

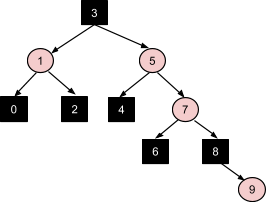
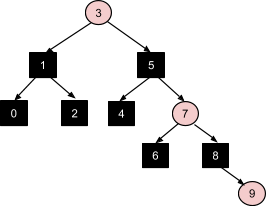
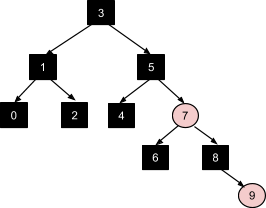
В результате получаем красно-черное дерево, у которого высота любого поддерева не превышает высоту братского поддерева более чем в 2 раза, что позволяет сохранить логарифмическую вычислительную сложность всех операций.

Реализация удаления узлов из красно-черного дерева является еще более громоздкой чем вставка. Основная идея аналогична - в результате выполнения базового алгоритма удаления узла из BST может быть нарушено одно из свойств красно-черного дерева, которое следует незамедлительно восстановить при помощи перекрашиваний и вращений. Более подробно об этом алгоритме можно прочесть в литературе, например, в книге Т. Кормена в главе №13 “Красно-черные деревья”, пункт 13.4 “Удаление”.

Выводы

В данной лекции был рассмотрен популярный алгоритм бинарных деревьев поиска (BST), имеющий широкое практическое применение благодаря логарифмической вычислительной сложности. Свойство упорядоченности ключей при симметричном обходе BST может быть использовано как один из возможных способов сортировки набора ключей. BST в худшем случае может выродиться до односвязного списка с линейной сложностью поиска, при условии вставки уже упорядоченных узлов. Улучшить поведение BST в такой ситуации могут алгоритмы, создающие сбалансированные деревья, например, красно-черные деревья.