Красно-черные деревья

Одним из наиболее популярных алгоритмов автоматической балансировки BST является алгоритм красно-черных деревьев. Обычно именно этот алгоритм используется при реализации стандартных библиотечных средств для отображений и множеств на основе BST.

Идея данного алгоритма состоит в расширении объекта-узла еще одной переменной, обозначающей цвет узла: красный или черный. Выбор таких названий является условным, смысл состоит в разделении всех узлов на 2 типа:

structRBTree

{

structNode

{

intm_key;

enumColor { RED, BLACK } m_color;

Node * m_pParent;

Node * m_pLeft;

Node * m_pRight;

};

Node * m_pRoot;

};

В любом состоянии красно-черное дерево должно сохранять следующие свойства, помимо характеристического свойства BST:

1. Корень дерева является черным узлом.
2. Если узел красный, его дочерние узлы могут быть только черными.
3. Для каждого промежуточного узла все пути от него до его листьев содержат одинаковое количество черных узлов.

Исходя из условий 2 и 3, можно сделать вывод, что при соблюдении всех условий, высота левого и правого поддерева в самом худшем случае отличается не более чем в 2 раза (за счет возможных дополнительных красных промежуточных узлов между черными узлами). Из этой структурной особенности вытекает, что операции вставки, поиска и удаления будут характеризоваться логарифмической вычислительной сложностью, а самои дерево будет приближенно сбалансированным.

Реализация функций создания и уничтожения дерева, поиска интересующего ключа, минимального и максимального ключей, вращения узлов, обхода - ни чем не отличается от рассмотренной выше базовой реализации бинарных деревьев поиска. Принципиально отличаются только операции вставки и удаления узлов, поскольку должны сохраняться дополнительные, по сравнению с BST, свойства.

Подробно рассмотрим алгоритм вставки. Каждый новый вставляемый узел должен быть изначально назначен красным. В начале выполняются обычные действия по вставке ключа в BST, как и в базовой реализации, а затем запускается дополнительная процедура, обеспечивающая сохранение специальных свойств красно-черных деревьев. Собственно, после вставки необходимо выявлять возможные проблемы двух типов:

• корень красного цвета;
• красный дочерний узел прикреплен к красному узлу-родителю.

Первая проблема решается путем перекраски корневого узла в черный цвет. Вторая проблема сложнее, и следует рассмотреть несколько случаев ее решения:

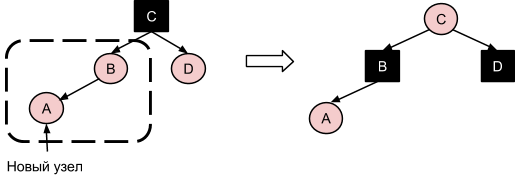
1. Новый красный узел A прикрепляется к родительскому красному узлу B слева, а также имеется узел-”дядя” D, который также является красным. Следует перекрасить узлы B и D в черный цвет, а узел-”дед” C - наоборот в красный:

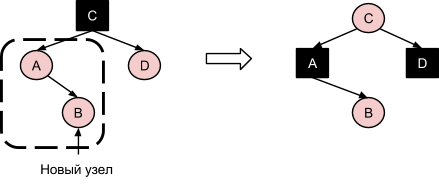
2. Новый красный узел B прикрепляется к родительскому красному узлу A справа, а также имеется узел-”дядя” D, который также является красным. Аналогично, следует перекрасить узлы A и D в черный цвет, а узел-”дед” C - в красный:

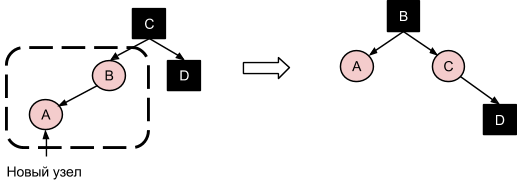
3. Новый красный узел A прикрепляется к родительскому красному узлу B слева, а узла-”дяди” D в дереве либо нет, либо он является черным. Следует осуществить вращение по оси между узлами B и C, поменяв их цветами:

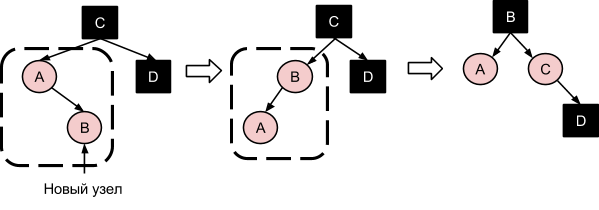
4. Новый красный узел B прикрепляется к родительскому красному узлу A справа, , а узла-”дяди” D в дереве нет, либо он является черным. Следует осуществить вращение по оси между узлами A и B, а затем свести задачу к предыдущему случаю:

Возможны также зеркально симметричные случаи, которые разрешаются аналогично.

В результате применения правил коррекции №1 и №2 на основе вращений, нарушение свойств красно-черного дерева может повториться для узлов, находящихся выше по иерархии, т.к. в результате получается поддерево с красным корнем. В таком случае все корректирующие операции алгоритма следует повторно применить на следующем уровне и так далее, пока дерево в итоге не стабилизируется.

Ниже представлен программный код, реализующий описанный алгоритм вставки с коррекциями:

// Функция создания нового элемента красно-черного дерева

RBTree::Node * RBTreeCreateNode ( int_key )

{

RBTree::Node * pNewNode = new RBTree::Node;

pNewNode->m_key = _key;