Ориентированные деревья.

Задача коммивояжера, задача о минимальной раскраске графа.

Деревья. Свободные деревья. Основные свойства деревьев.

Граф без циклов называют ациклическим или лесом. Связный ациклический граф называют деревомили свободным деревом. Компонентами связности леса являются деревья.

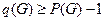В связном графе выполняется неравенство , где 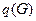– количество ребер, 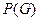– количество вершин. Граф , в котором выполняется равенство 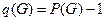называют древовидным.

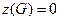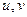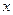В ациклическом графе число циклов . Пусть – несмежные вершины графа и пусть – ребро, которое может быть образовано между вершинам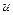и и 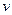, не принадлежит множеству ребер графа , 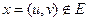. Если граф 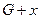имеет только один простой цикл, 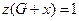, то граф называется субциклическим.

Пример: свободные деревья с пятью вершинами.

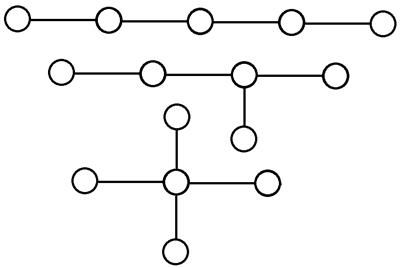
Свойства деревьев.

Теорема о свойствах деревьев устанавливает, что два из четырех свойств – связность, ацикличность, древовидность и субцикличность – характеризуют граф как дерево.

Теорема.Пусть 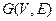– граф с 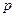вершинами, 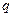ребрами, 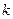компонентами связности и простыми циклами. Пусть 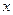– ребро, соединяющее любую пару несмежных вершин в графе . Тогда следующие утверждения эквивалентны:

1. – дерево, т.е. связный граф без циклов,

;

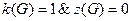2. Любые две вершины соединены в графе единственной простой цепью,

;

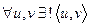3. – связный граф, и любое ребро есть мост,

;

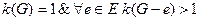4. Граф – связный и древовидный,

;

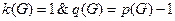5. Граф – ациклический и древовидный,

;

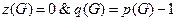6. Граф – ациклический и субциклический,

;

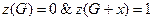7. Граф – связный, субциклический и неполный,

;

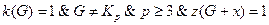8. Граф – древовидный и субциклический (за двумя исключениями),

.

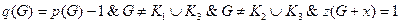Ориентированные деревья.

Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:

1. Существует единственный узел 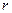, полустепень захода которого равна 0, 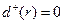. Он называется корнемордерева.

2. Полустепень захода всех остальных узлов равна единице, .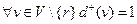

3. Каждый узел достижим из корня, .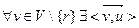

Пример: диаграммы ордеревьев с 3 узлами:

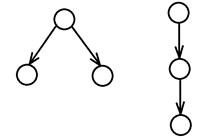
диаграммы ордеревьев с 4 узлами:

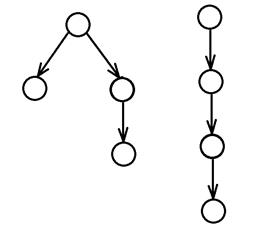
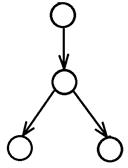
Свойства ордерева:

1. Число ребер на единицу меньше числа узлов, .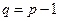

2. Если в ордереве забыть ориентацию ребер то получится свободное дерево.

3. В ордереве нет контуров.

4. Для каждого узла существует единственный путь, ведущий в этот узел из корня.

5. Подграф, определяемый множеством узлов, достижимых из узла 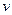, является ордеревом с корнем 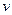(это ордерево называется поддеревом узла ).

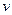6. Если в свободном дереве любую вершину назначить корнем, то получится ордерево.

Эквивалентное определение ордерева.

Ордерево 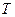– это конечное множество узлов, таких что:

1. Имеется один узел 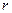, называемый корнем данного дерева.

2. Остальные узлы (исключая корень) содержатся в 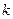попарно непересекающихся множествах 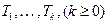, каждое из которых является ордеревом.

.

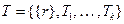Если относительный порядок поддеревьев фиксирован, то ордерево называется упорядоченным.

Пример: для представления выражений языков программирования, как правило, используются ориентированные упорядоченный деревья. Выражение :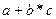

Бинарные деревья.

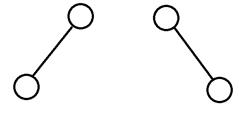
Бинарное (двоичное) дерево– это конечное множество узлов, которое либо пусто, либо состоит из корня и двух непересекающихся бинарных деревьев – левого и правого. Бинарное дерево не является упорядоченным ордеревом.

Пример: два различных бинарных дерева.

Всякое свободное дерево можно ориентировать, назначив один из узлов корнем. Всякое ордерево можно произвольно упорядочить. Для потомков одного узла (братьев) упорядоченного ордерева определено отношение старше-младше (левее-правее). Всякое упорядоченное дерево можно представить бинарным деревом, проведя правую связь к старшему брату, а левую – к младшему сыну.

Пример: диаграммы упорядоченного и соответствующего ему бинарного дерева.

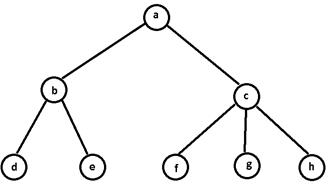
упорядоченное дерево бинарное дерево

Эйлеровы графы.

Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называют эйлеровым циклом, а граф называют эйлеровым графом.

Если граф имеет цепь (не обязательно простую), содержащую все ребра по одному разу, то такая цепь называется эйлеровой цепью, а граф называют полуэйлеровым графом.

Теорема.Если граф связен и нетривиален, то следующие утверждения эквивалентны:

1. – эйлеров граф.

2. Каждая вершина графа имеет четную степень.

3. Множество ребер графа можно разбить на простые циклы.

Теорема дает решение задачи о кенигсбергских мостах. Т.е. для того чтобы обойти все ребра по одному разу – степени все вершин должны быть четны.