Гамильтоновы циклы.
Название «гамильтонов цикл» произошло от задачи о кругосветном путешествии, придуманной Гамильтоном (1805-1856). С точки зрения теории графов она формулировалась следующим образом: нужно обойти все вершины графа по одному разу и вернуться в исходную точку. Граф представлял собой укладку додекаэдра.
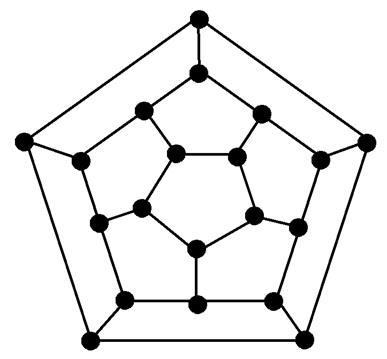
Если граф имеет простой цикл содержащий все вершины графа (по одному разу), то такой цикл называют гамильтоновым циклом, а граф называют гамильтоновым графом. Гамильтонов цикл не обязательно содержит все ребра графа.
Теорема Дирака.Если в графе 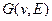 для любой вершины
для любой вершины 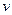 из множества
из множества 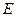 , степень вершины
, степень вершины 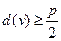 , то граф
, то граф  называется гамильтоновым.
называется гамильтоновым.
Задача коммивояжера.Имеется 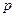 городов, расстояния между которыми известны. Коммивояжер должен посетить все
городов, расстояния между которыми известны. Коммивояжер должен посетить все 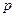 городов по одному разу вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным.
городов по одному разу вернувшись в тот, с которого начал. Требуется найти такой маршрут движения, при котором суммарное пройденное расстояние будет минимальным.
Задача коммивояжера – задача отыскания кратчайшего гамильтонова цикла в полном графе.
Задача о минимальной раскраске графа.
Раскраской графа называется такое предписывание цветов (натуральных чисел) его вершинам, что никакие две смежные вершины не получают одинаковых цветов.
Наименьшее возможное число цветов в раскраске называют хроматическим числом и обозначают 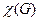 . Очевидно, что существует некоторая
. Очевидно, что существует некоторая 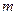 -раскраска графа, причем
-раскраска графа, причем 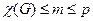 .
.
Множество вершин, покрашенных в один цвет, называют одноцветным классом. Одноцветные классы образуют независимые множества вершин, т.е. никакие две вершины в одноцветном классе не смежны.
Пример: хроматические числа для различных графов.
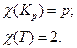
Для хроматического числа доказана теорема: 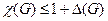 , где
, где 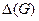 – максимальная степень свободных вершин графа.
– максимальная степень свободных вершин графа.
Говорят, что граф укладывается на некоторой поверхности, если его можно нарисовать на этой поверхности так, чтобы ребра графа при этом не пересекались.
Граф называется планарным, если его можно уложить на плоскости. Плоский граф – граф  , уложенный на плоскости.
, уложенный на плоскости.
Область, ограниченная ребрами в плоском графе и не содержащая внутри себя вершин и ребер называется гранью. Грань не содержит других граней. Число граней плоского графа обозначают 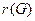 .
.
Для графов, уложенных на некоторой поверхности, справедливо определенное соотношение между числом вершин, рёбер и граней графов, которые укладываются на этой поверхности. Это отношение называется эйлеровой характеристикой поверхности или формулой Эйлера.
Пример: является ли граф 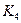 планарным?
планарным?


Является.
На рисунке представлены планарный граф и его укладка. 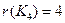 .
.
В связном планарном графе справедливо следующее (формула Эйлера): 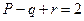 .
.
Для нашего примера:, 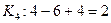 .
.
Если граф  – связный планарный граф, где
– связный планарный граф, где 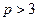 , то
, то 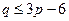 .
.
Теорема о пяти красках.Всякий планарный граф можно раскрасить пятью красками.
Алгоритм раскрашивания: рассмотрим следующую схему рекурсивной процедуры 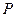 .
.
1. Выбрать в графе  некоторое максимальное независимое множество вершин
некоторое максимальное независимое множество вершин 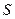 .
.
2. Покрасить вершины множества 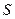 в очередной цвет.
в очередной цвет.
3. Применить процедуру 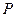 к графу
к графу 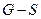 .
.
Дата добавления: 2015-12-16; просмотров: 2344;
