Эйлеровы и Гамильтоновы графы

Связный граф называется эйлеровым, если существует замкнутая цепь, проходящая через каждое его ребро ровно по одному разу.

Такая цепь называется эйлеровой цепью.

Теорема. (Гамильтон). Граф 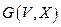является эйлеровым тогда и только тогда, когда:

1) он связен;

2) степени всех его вершин четные.

Если в связном графе не требовать замкнутости цепи, проходящей по всем ребрам, то граф называется полуэйлеровым.

Теорема. Для того чтобы в графе 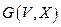существовала полуэйлерова цепь, соединяющая вершины 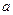и , необходимо и достаточно, чтобы эти вершины были единственными вершинами графа G, имеющими нечетные степени.

Алгоритм Флери (алгоритм построения эйлеровой цепи в заданном эйлеровом графе) задается следующей теоремой:

Теорема. Пусть 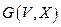– эйлеров граф. Тогда следующая процедура всегда возможна и приводит к нахождению эйлеровой цепи графа G:

Выходя из произвольной вершины 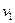, идем по ребрам графа произвольным образом, соблюдая следующие правила:

1) «стираем» ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются (при этом фиксируем пройденный маршрут);

2) на каждом этапе в оставшемся графе мы идем по мосту только в том случае, если нет другой возможности.

Если в связанном графе 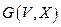существует цикл, проходящий ровно один раз через каждую вершину, то он называется гамильтоновым циклом, а граф 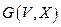– гамильтоновым графом.

Полугамильтоновый граф – не требует замкнутости.

Теорема (Дирак). Если в простом графе с n вершинами 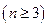степень любой вершины то граф является гамильтоновым.

§6. Сетевые модели планирования и управления

Сетевой моделью (сетевым графиком, сетью) называется экономико-компьютерная модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи.

Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет,

во-первых, более четко выявить взаимосвязи этапов реализации проекта и

во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ.

Таким образом, методы сетевого моделирования относятся к методам принятия оптимальных решений, что оправдывает рассмотрение этого типа моделей в данной курсовой работе.

В экономических исследованиях сетевые модели возникают при моделировании экономических процессов методами сетевого планирования и управления (СПУ).

Объектом управления в системах сетевого планирования и управления являются коллективы исполнителей, располагающих определенными ресурсами и выполняющих определенный комплекс операций, который призван обеспечить достижение намеченной цели, например, разработку нового изделия, строительства объекта и т.п.

Основой сетевого планирования и управления является сетевая модель (СМ), в которой моделируется совокупность взаимосвязанных работ и событий, отображающих процесс достижения определенной цели. Она может быть представлена в виде графика или таблицы.

Основным понятия сетевой модели являются:

· событие,

· работа

· путь.

На Рис. 1 графически представлена сетевая модель, состоящая из 11 событий и 16 работ, продолжительность выполнения которых указана над работами.

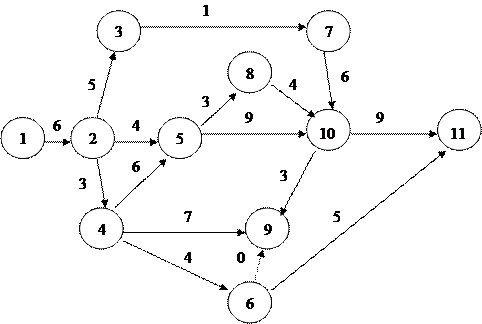
Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. При графическом представлении работа изображается стрелкой, которая соединяет два события. Она обозначается парой заключенных в скобки чисел 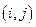, где i - номер события, из которого работа выходит, а j - номер события, в которое она входит. Работа не может начаться раньше, чем свершится событие, из которого она выходит. Каждая работа имеет определенную продолжительность 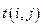. Например, запись 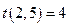означает, что работа (2,5) имеет продолжительность 5 единиц.

К работам относятся также такие процессы, которые не требуют ни ресурсов, ни времени выполнения. Они заключаются в установлении логической взаимосвязи работ и показывают, что одна из них непосредственно зависит от другой; такие работы называются фиктивными и на графике изображаются пунктирными стрелками (работа (6,9)).

Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени. Событие свершается в тот момент, когда оканчивается последняя из работ, входящая в него. События обозначаются одним числом и при графическом представлении сетевая модель изображаются кружком (или иной геометрической фигурой), внутри которого проставляется его порядковый номер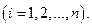

В сетевой модели имеется начальное событие (с номером 1), из которого работы только выходят, и конечное событие (с номером N), в которое работы только входят.

Путём называется цепочка следующих друг за другом работ, соединяющих начальную и конечную вершины, например, в приведенной выше модели путями являются 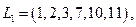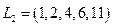и др.

Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь, имеющий максимальную длину, называют критическим и обозначают , а его продолжительность - 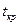. Работы, принадлежащие критическому пути, называются критическими. Их несвоевременное выполнение ведет к срыву сроков всего комплекса работ.

Cетевая модель имеют ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.

Перед расчетом СМ необходимо убедиться, что она удовлетворяет следующим основным требованиям:

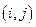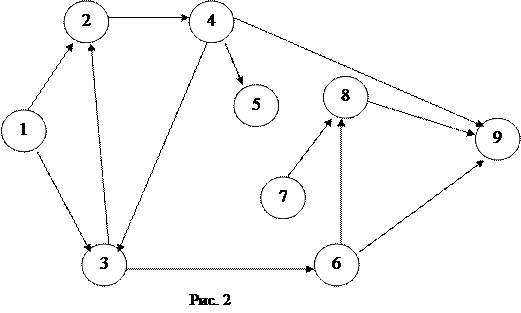
1. События правильно пронумерованы, т. е. для каждой работы справедливо неравенство 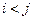(например, на Рис. 2 работы (4,3) и (3,2)). При невыполнении этого требования необходимо использовать алгоритм перенумерации событий, который заключается в следующем:

· нумерация событий начинается с исходного события, которому присваивается № 1;

· из исходного события вычеркивают все исходящие из него работы (стрелки), и на оставшейся сети находят событие, в которое не входит ни одна работа, ему и присваивают № 2;

· затем вычеркивают работы, выходящие из события № 2, и вновь находят событие, в которое не входит ни одна работа, и ему присваивают № 3, и так далее до достижения завершающего события, номер которого должен быть равен количеству событий в сетевом графике.

Если при очередном вычеркивании работ одновременно несколько событий не имеют входящих в них работ, то их нумеруют очередными номерами в произвольном порядке.

2. Отсутствуют тупиковые события (кроме завершающего), т. е. такие, за которыми не следует хотя бы одна работа (например, событие 5);

3. Отсутствуют события (за исключением исходного), которым не предшествует хотя бы одна работа (например, событие 7);

4. Отсутствуют циклы, т. е. замкнутые пути, соединяющие событие с ним же самим (например, путь (2,4,3)).

Только после выполнении всех указанных требований можно приступать к вычислениям характеристик событий, работ и критического пути.