ГРАФЫ ЭЛЕКТРОННЫХ СХЕМ
При анализе электронных схем методом графов роль сигналов вершин играют токи и напряжения. Для любой схемы всегда можно записать уравнения для некоторой совокупности токов и напряжений этой схемы. Коэффициенты полученных уравнений, имеющие размерности сопротивления, проводимости или безразмерные, представляют собой не что иное, как передачи ветвей соответствующего графа. Число вершин графа всегда равно количеству различных токов и напряжений, выбранных для описания схемы. Число ветвей графа равно общему количеству слагаемых в правых частях уравнений. Причем, токи и напряжения на входах схемы являются сигналами источников (истоков) графа.
Так как уравнения схемы можно записать в различной форме, то и соответствующие графы могут иметь различную конфигурацию. Но при всех вариантах для одной и той же схемы должны получаться эквивалентные графы, отображающие один и тот же закон передачи сигналов от источников (истоков) к стокам.
Пример 6.1. Рассмотрим порядок построения графа для схемы каскодного усилителя на полевых транзисторах (рис 6.4).
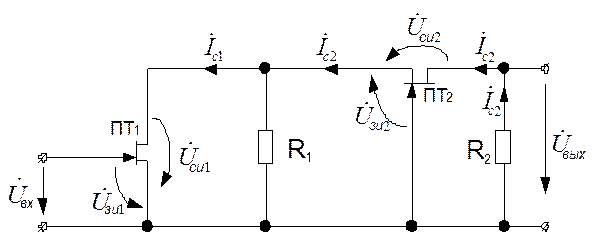
Рисунок 6.4
Схема представлена для переменных составляющих токов и напряжений. Транзисторы работают при отрицательных напряжениях смещения на затворах (ток затвора равен нулю) и работу транзистора описывают уравнения:
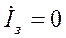 ;
; 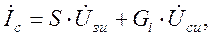
где 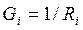 –- проводимость полевого транзистора.
–- проводимость полевого транзистора.
При построении графа в качестве вершин выбираем:
а) токи транзисторов – 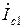 и
и 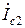 ;
;
б) напряжения затвор-исток – 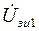 и
и 
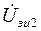 ;
;
в) напряжение сток-исток – 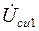 и
и 
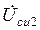 ;
;
г) выходное напряжение схемы – 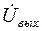 ;
;
д) входное напряжение – 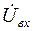 .
.
Записываем уравнения, описывающие работу схемы. Запись начинаем с выходного напряжения схемы; затем последовательно записываем уравнения для токов и напряжений, которые входят в правые части предыдущих уравнений:
а) 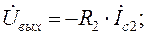
б) 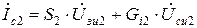
в) 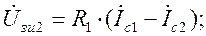
г) 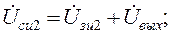
д) 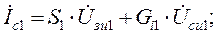
е) 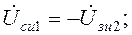
ж) 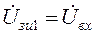 .
.
Последовательно отображая эти уравнения, получаем искомый граф (рис 6.5):
| а) | 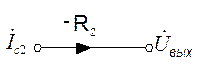
|
| б) | 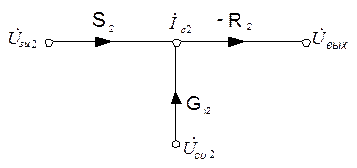
|
| в) | 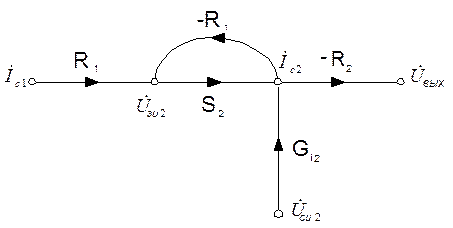
|
| г) | 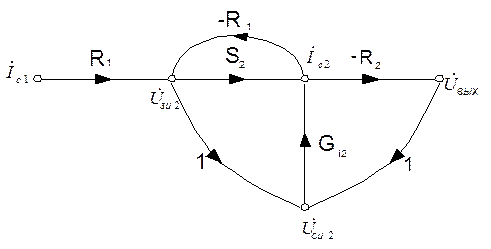
|
| д) | 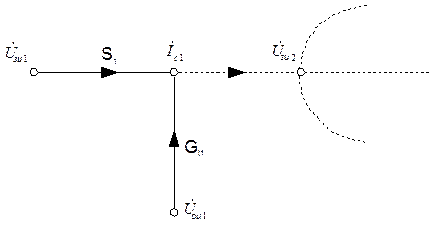
|
| е) | 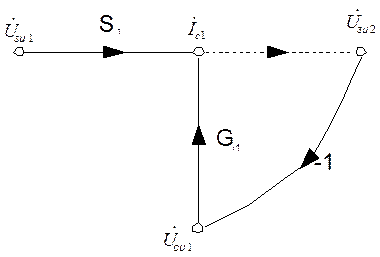
|
В результате получаем граф, представленный на рис. 6.5.
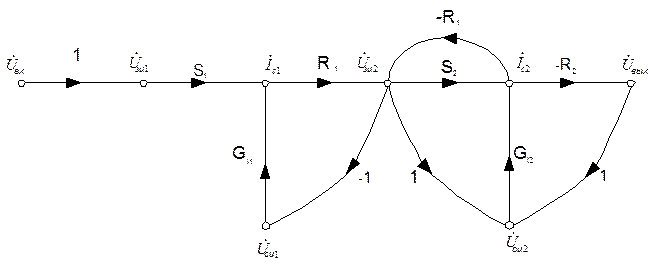
Рисунок 6.5
Пример 6.2. Если исходить из уравнения для напряжения сток-исток транзистора:
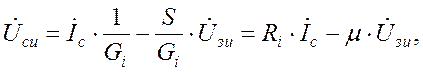
то уравнения для рассмотренной схемы будут иметь вид:
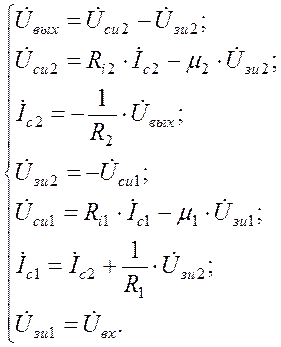
Граф, соответствующим этим уравнениям, приведен на рис. 6.6.
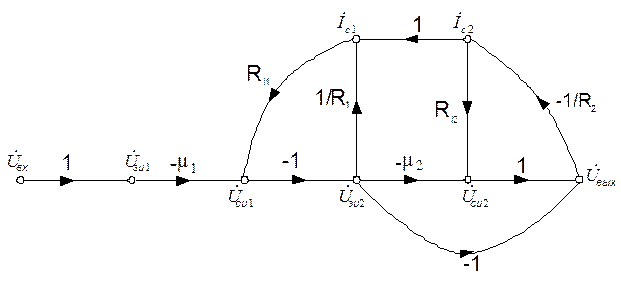 Рисунок 6.6
Рисунок 6.6
Используя одну из форм записи уравнений транзистора, как четырехполюсника, можно построить подграфы транзистора. Например:
а) Y- параметры:
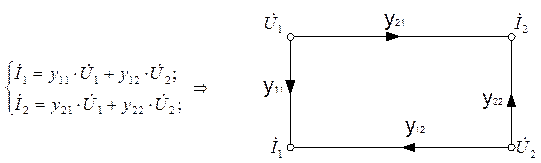
б) h-параметры:
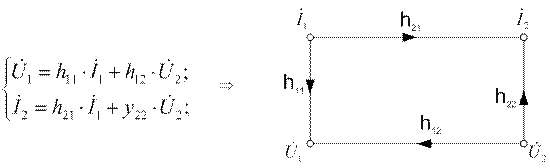
и.т.д.
Пример 6.3. Построить сигнальный граф для схемы однокаскадного транзисторного усилителя, приведенной на рис. 6.7.
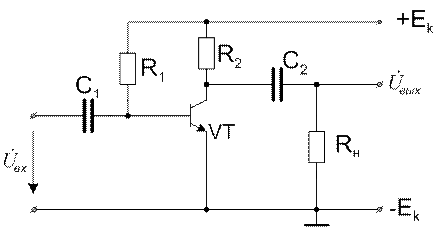
Рисунок 6.7
1) Составляем рабочую (схему для переменных составляющих сигнала)
и указываем в ней соответствующие токи и напряжения (рис. 6.8).
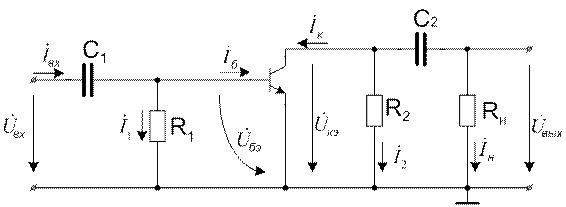
Рисунок 6.8
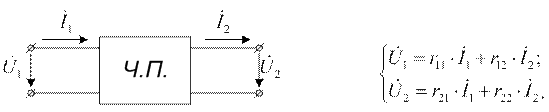
2)При записи системы уравнений данной схемы воспользуемся уравнениями транзистора, записанными в системе r-параметров. Схема четырехполюсника и система уравнений в r-параметрах для него приведена ниже:
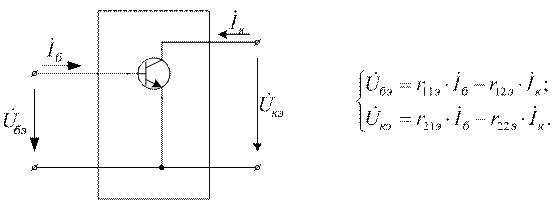
Биполярный транзистор в схеме с ОЭ, как четырехполюсник, и соответствующая система уравнений для него имеют вид:
В последних уравнениях вторые слагаемые в правых частях уравнений записаны со знаком "минус", т.к. ток 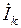 в схеме транзистора направлен противоположно току
в схеме транзистора направлен противоположно току 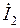 в схеме четырехполюсника.
в схеме четырехполюсника.
3) Записываем систему уравнений для схемы рис. 6.8:
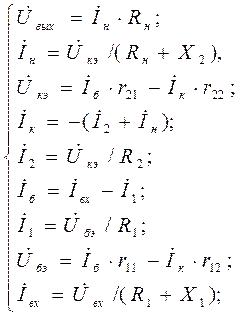
где 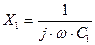 и
и 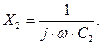
4) Используя систему уравнений, строим граф схемы:

6.3 ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФОВ
1) Последовательное соединение двух одинаково направленных ветвей может быть заменено одной ветвью, передача которой равна произведению передач исходных ветвей:
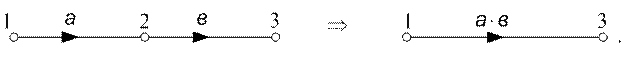
2) При параллельном соединении двух одинаково направленных ветвей передача эквивалентной ветви равна сумме передач исходных ветвей; при этом число вершин остается неизменным, а граф упрощается за счет устранения ветви:

Правила 1 и 2 могут быть распространены на любое количество ветвей.
3)Пусть к некоторой вершине подходит несколько ветвей и несколько ветвей выходит из нее. Если в этой вершине отсутствуют петли, то после ее устранения каждая входная вершина будет связана с каждой выходной вершиной ветвью, передача которой равна произведению передач ветвей, расположенных между ними внутренней вершиной:
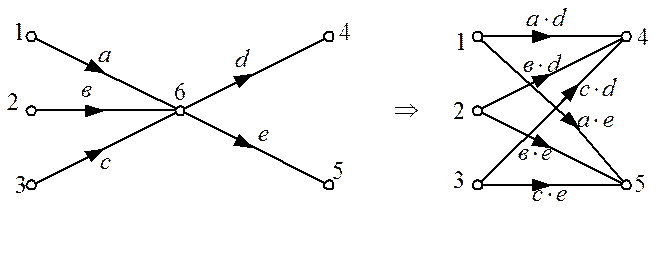
4) Исключение петли графа.
а) Пусть устраняемая вершина содержит петлю.
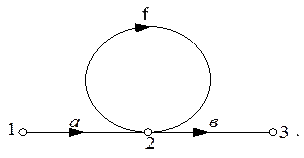
Записываем уравнения для вершин графа: x2=ax1+fx2; x3=bx2.
Из первого уравнения определим x2 и подставим во второе:
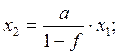
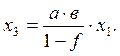
Этому уравнению соответствует граф: 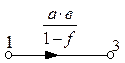 .
.
Сравнивая полученный результат с правилом 1 заключаем, что при наличии в устраняемой вершине петли с передачей f, передач эквивалентной ветви умножается на 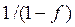 .
.
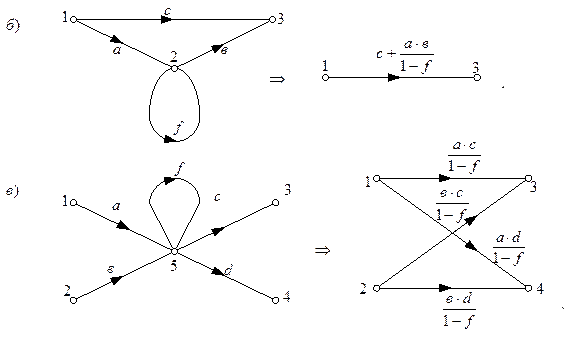
5) Исключение параллельно включенных ветвей графа.
Пусть с одной вершиной графа связаны только входящие ветви, а с другой только выходящие ветви, а между этими вершинами есть ветви, направленные различно относительно вершин – рис.6.9а. Применяя правило 3 относительно вершины х5, устраняем эту вершину; при этом образуется петля в вершине х6– рис. 6.9б. Применяем правило 4 устранения вершины х6 с петлей в ней, получаем эквивалентный граф на рис. 6.9в.
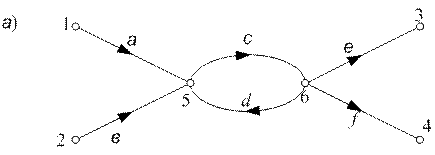
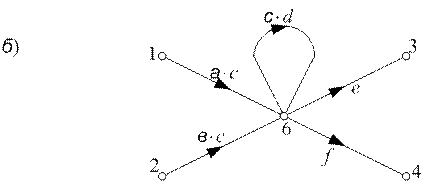
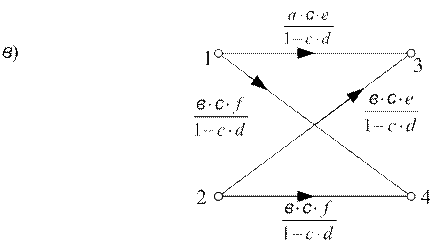
Рисунок 6.9
6) Если граф представляет последовательно-параллельное соединение ветвей и параллельные ветви разнонаправленные (рис.6.10а), то упрощение графа следует начинать с внешних вершин x2 и x5 (рис. 6.10б). При этом получаются петли, которые учитываются (устраняются) при последующих преобразованиях (рис.6.10в).

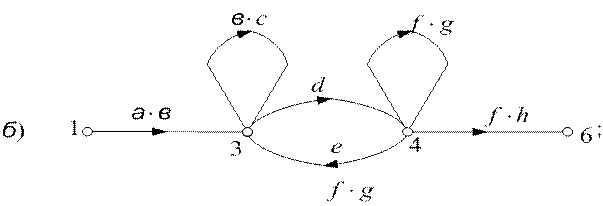
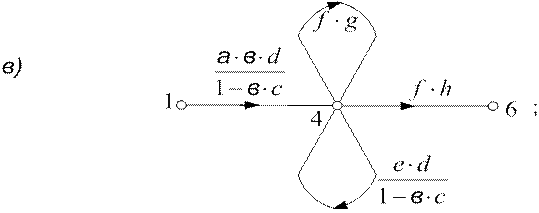
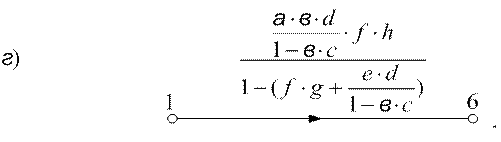
Рисунок 6.10
Если же упрощение графа рис. 6.10а начинать с одной из внутренних вершин, то процедура значительно усложняется.
7) Часто полезными оказываются следующие преобразования: они позволяют упростить граф путем исключения одной из вершин (х4 - в приведенных примерах).

Пример 6.4. Упростим граф и определим коэффициент передачи по напряжению каскадного усилителя (рис. 6.4). В качестве исходного используем граф, подобный приведенному на рис. 6.6. Исходный граф имеет вид:
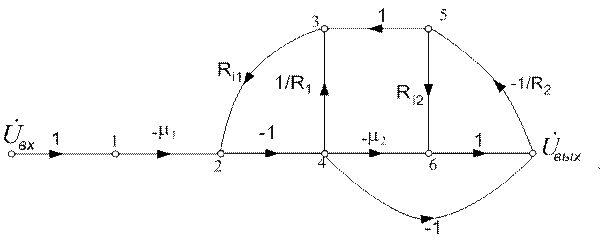
а) Устраняем ветвь графа между вершинами x3 и x5 :
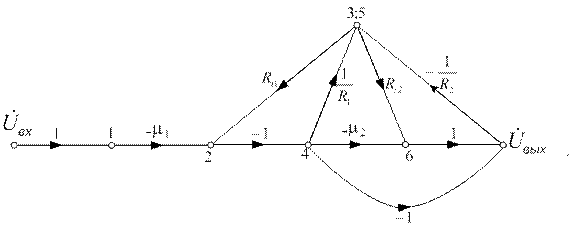
б) Избавляемся от вершины x3 (или x5):
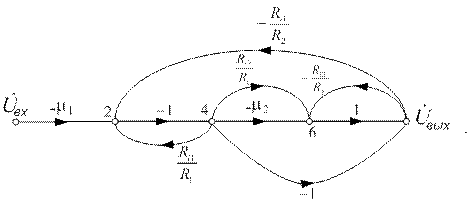
в) Заменяем две одноправные ветви между вершинами x4 и x6 одной эквивалентной:
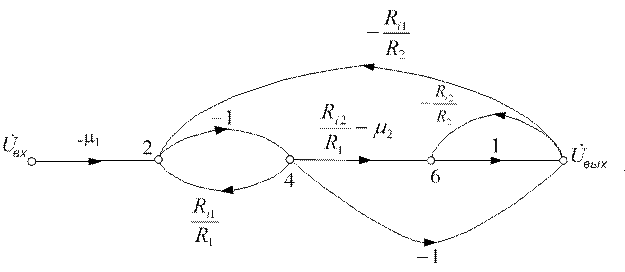
г)Устраняем вершину x6 :
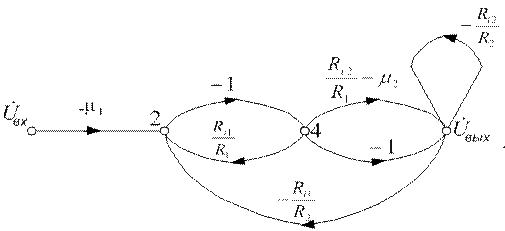
д)Устраняем вершину x2 и одновременно заменяем две одноправные ветви между вершинами x4 и 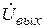 одной эквивалентной:
одной эквивалентной:
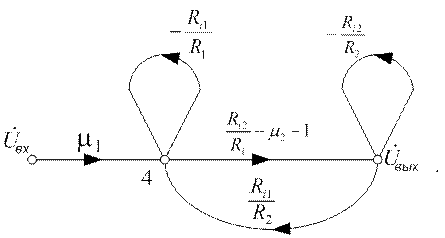
е) Избавляемся от вершины x4:
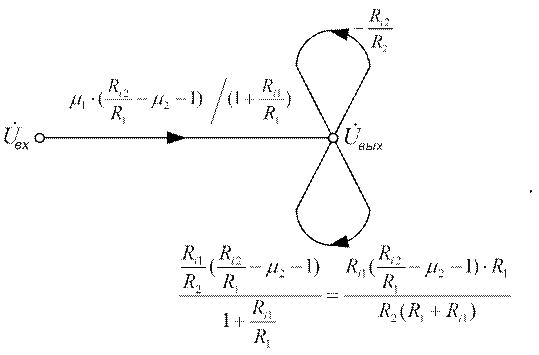
ж) Введем обозначения для элементов последнего графа:
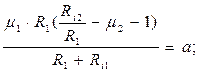
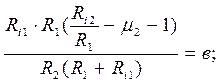
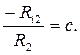
Тогда получим граф:
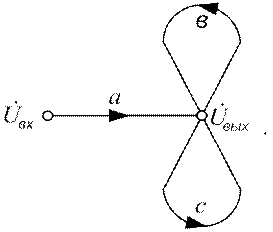
Для этого графа можно записать:
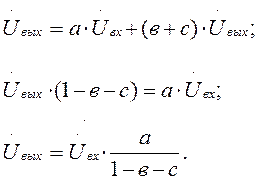
Откуда:
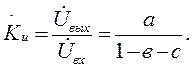
6.4 ПЕРЕДАЧА ГРАФА
Передачу сигнала от источника (истока) графа к какой-либо вершине, выбранной в качестве стока, можно получить путем последовательных упрощений графа до одной ветви (как это сделано в предыдущем примере). Однако зачастую этот путь оказывается громоздким. Кроме того, получаемые аналитические выражения имеют при этом вид многоэтажных дробей, что неудобно для последующего анализа. В тоже время существует возможность определять передачу сигнала от источника к стоку непосредственно из рассмотрения графа без его преобразований. Получим общую формулу.
Обозначим через x0- сигнал источника, а остальные вершины графа пронумеруем цифрами от 1 до n; соответствующие сигналы вершин графа обозначим x1, x2...xn.Уравнения для каждого из этих сигналов (кроме сигнала источника) имеют вид:
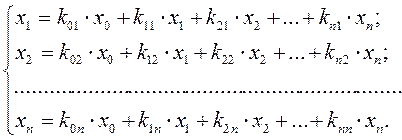 (6.2)
(6.2)
Здесь k01,k02,...,k0n – передачи ветвей от источника до соответствующих вершин графа, на который указывает второй индекс; kij - передача ветви, направленной от i-й к j-ой вершине; kii - передача ветви в i-ой вершине.
Произведения k01x0, k02x0,...,k0nx0 можно рассматривать как некоторые задающие величины, которые определяют воздействие источника на граф. Определив эти произведения из уравнений (6.2) путем соответствующих преобразований и разделив обе части полученных уравнений на x0, получим:
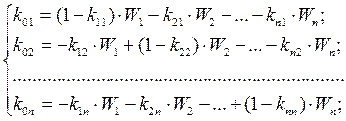 (6.3)
(6.3)
где Wi=xi /x0 – передача графа от источника к i-ой вершине.
В матричной форме эти уравнения можно записать:
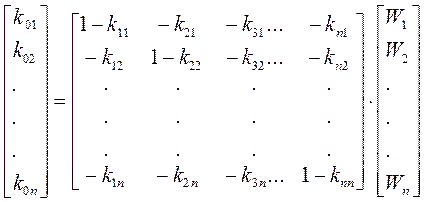 (6.4)
(6.4)
или : 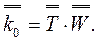 (6.5)
(6.5)
Здесь: 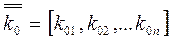 и
и 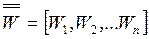 –n-мерные векторы;
–n-мерные векторы; 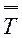 –квадратная матрица n-го порядка, называемая матрицей графа.
–квадратная матрица n-го порядка, называемая матрицей графа.
Из уравнения (6.5) может быть определен вектор передачи графа:
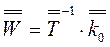 . (6.6)
. (6.6)
Передача графа от источника к i-ой вершине, т.е. i-я компонента вектора 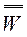 определяется:
определяется:
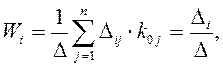 (6.7)
(6.7)
где D - определитель матрицы графа, называемый определителем графа; Dij- алгебраическое дополнение элемента Tji этой матрицы; Di - определитель матрицы, получаемой из матрицы 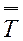 путем замены i-го столбца столбцом
путем замены i-го столбца столбцом 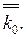 Записав для рассматриваемого графа матрицу
Записав для рассматриваемого графа матрицу 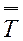 и вектор
и вектор 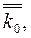 по формуле (6.7) можно определить интересующую передачу графа.
по формуле (6.7) можно определить интересующую передачу графа.
Пример 6.5. Получить выражение для определения коэффициента передачи по напряжению каскадного усилителя, граф которого приведен ниже.
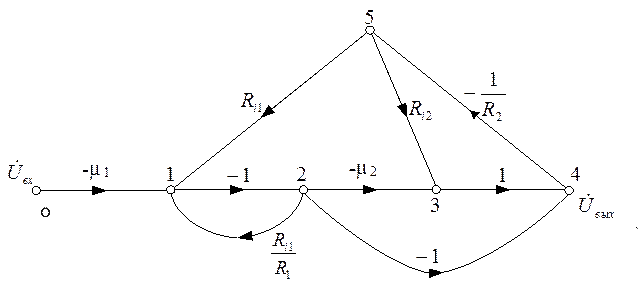
а) Записываем матрицу и задающий вектор графа:
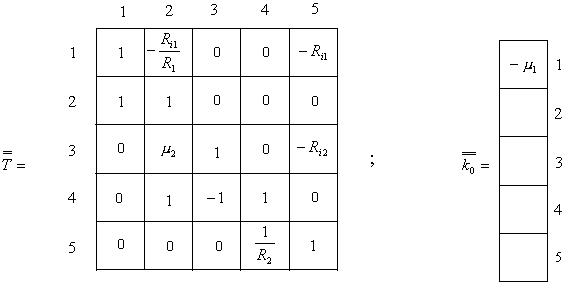
В данном примере сток графа соответствует вершине х4, т.е. в формуле (6.7) 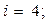 единственная отличная от нуля компонента задающего вектора
единственная отличная от нуля компонента задающего вектора 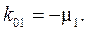 Поэтому
Поэтому
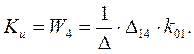
б) Определяем определитель матрицы 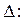
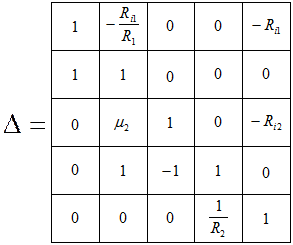 .
.
К первой строке этого определителя прибавляем вторую строку с противоположным знаком:
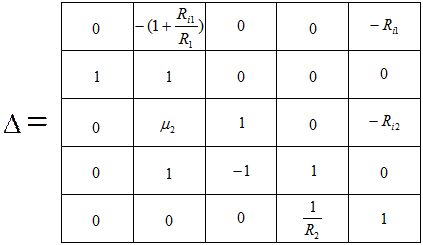 .
.
Раскрываем полученный определитель по первому столбцу:
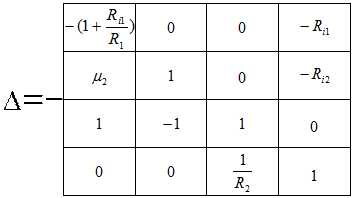 .
.
Раскрываем полученный определитель по первой строке:

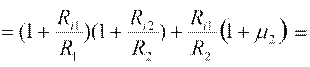
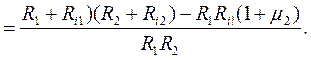
в) Определяем значение определителя 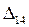 (в определителе
(в определителе 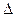 вычеркиваем 1-ю строку и 4-й столбец; полученный определитель умножаем на (-1)1+4 = (-1)5):
вычеркиваем 1-ю строку и 4-й столбец; полученный определитель умножаем на (-1)1+4 = (-1)5):
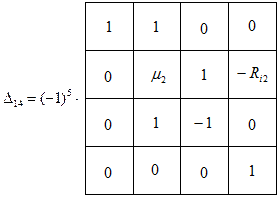
Раскрываем полученный определитель по первому столбцу:
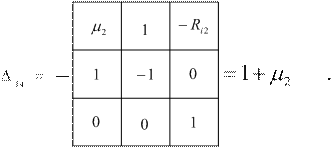
г) Выражение для определения Кu имеет вид:
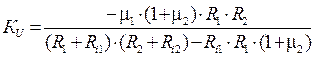 .
.
6.5 ПРИМЕНЕНИЕ МЕТОДА НАПРАВЛЕННЫХ ГРАФОВ
К АНАЛИЗУ ЭЛЕКТРОННЫХ СХЕМ
Формула передачи графа позволяет записать выражение для требуемой функции схемы непосредственно из рассмотрения графа. Во многих случаях так поступать удобнее, чем приводить граф к эквивалентной ветви путем ряда последовательных преобразований. Однако часто бывает полезно предварительно упростить исходный граф, прежде чем применять общую формулу.
Таким образом, анализ схемы методом направленных графов сводится к выполнению следующих операций:
1)составлению графа схемы с одним или несколькими источниками, выбранными в соответствии с условием задачи;
2)частичному упрощению графа (если это требуется) путем эквивалентных преобразований;
3)записи требуемой функции схемы по общей формуле передачи графа.
Пример 6.6 Построить граф и определить Ku усилительного звена
(рис. 6.11) с простой низкочастотной коррекцией (путем эквивалентных преобразований графа и путем применения формулы передачи графа).
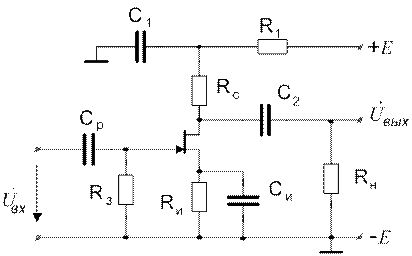
Рисунок 6.11.
а) Рабочая схема усилительного звена (схема для переменных составляющих сигнала) приведена на рис. 6.12.
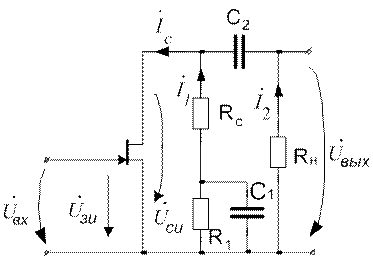
Рисунок 6.12.
б)Используя уравнение полевого транзистора
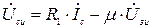
записываем систему уравнений для построения графа:
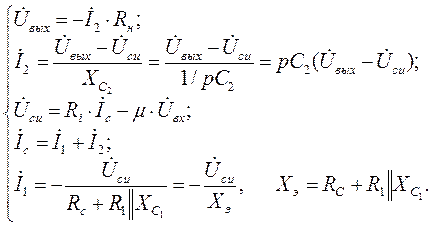
в) Строим граф схемы, используя полученную систему уравнений:
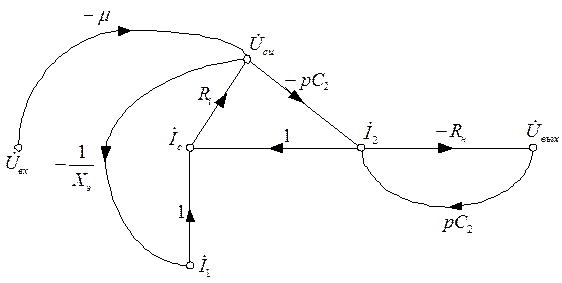
Рисунок 6.13.
г) Для определения 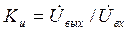 надо преобразовывать граф до вида одной ветви, содержащей 2 вершины -
надо преобразовывать граф до вида одной ветви, содержащей 2 вершины -  и
и 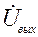 . После устранения вершины I1 получаем граф, приведенный на рис. 6.14:
. После устранения вершины I1 получаем граф, приведенный на рис. 6.14:
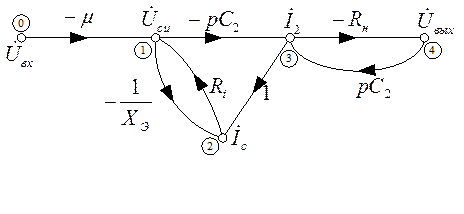
Рисунок 6. 14.
Избавляемся от вершины 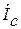 . Получаем граф:
. Получаем граф:
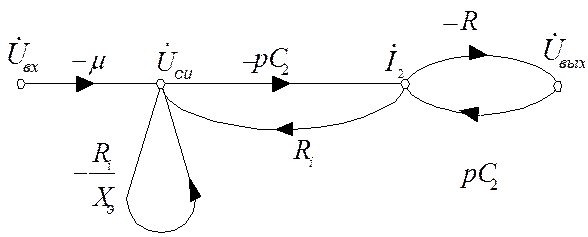
Устраняем вершину 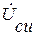 . Получаем граф:
. Получаем граф:
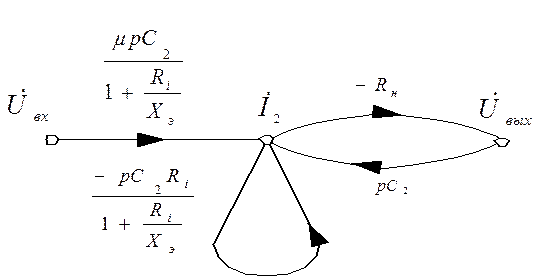
Введём обозначение 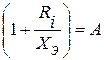 . Устраняем вершину
. Устраняем вершину 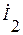 :
:
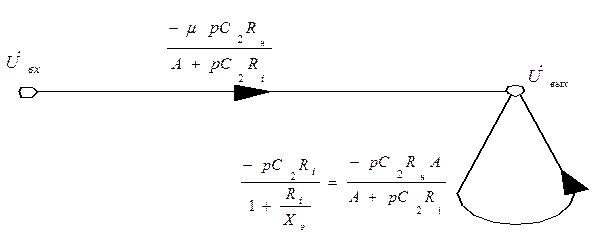
Для приведенного выше графа записываем уравнение для выходной вершины:
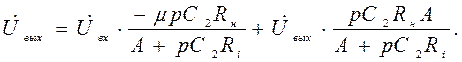
Преобразуем уравнение:
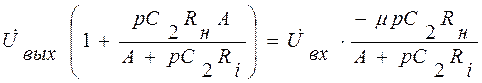
Используя это уравнение определяем 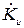 :
:
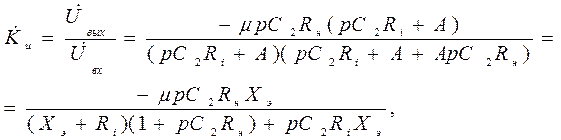
где 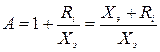 .
.
е) Воспользуемся формулой передачи графа для определения Ku. Записываем матрицу графа и задающий вектор, воспользовавшись графом, приведенным на рис.6.14. Здесь и ниже приняты следующие обозначения сигналов вершин графа: 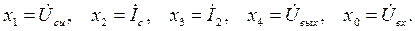
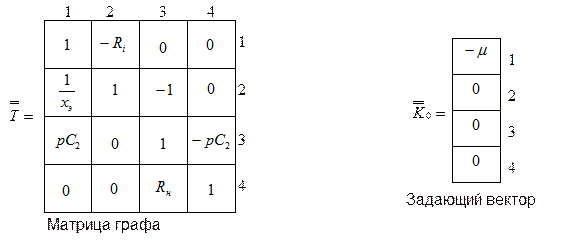
ж)
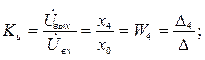
Определители 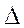 и
и 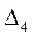 записаны ниже на основе применения матрицы и задающего вектора графа:
записаны ниже на основе применения матрицы и задающего вектора графа:

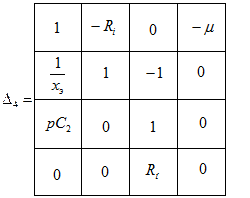
Раскрыв 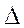 и
и 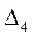 , используя приведенную выше формулу, можно определить KU.
, используя приведенную выше формулу, можно определить KU.
з) Можно воспользоваться более простым графом, чем рис. 6.14 (например, после устранения вершины 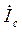 ):
):
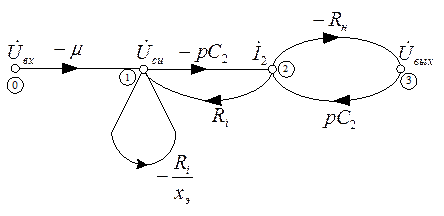
В этом случае:
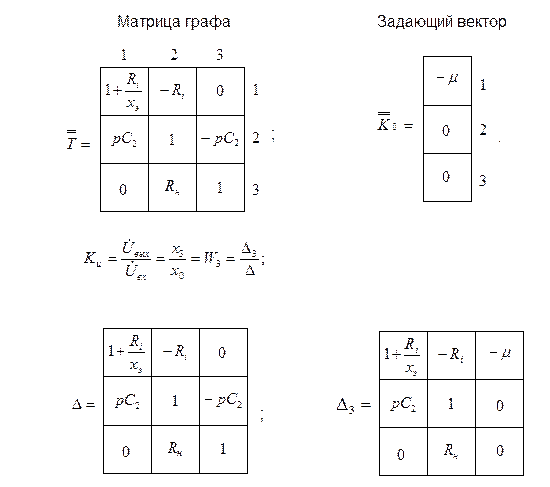
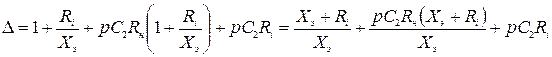 ;
;
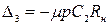 ;
;
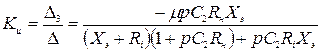 .
.
Дата добавления: 2016-01-03; просмотров: 3250;
