Анализа электронных схем

Краткая характеристика линейных методов

С помощью линейных методов анализа можно определять переменные составляющие токов и напряжений электронных схем или получать вторичные параметры схем. При этом полагается, что характеристики усилительных элементов схем в рабочей области достаточно близки к линейным. Предварительно принципиальная схема по возможности упрощается – составляется рабочая схема, справедливая для переменных составляющих токов и напряжений. При этом: а) выходные сопротивления источников питания схемы принимаются равными нулю; б) в зависимости от частоты сигнала можно пренебречь некоторыми реактивными элементами схемы (например, разделительной ёмкостью на высоких частотах, индуктивностью рассеяния трансформатора на низких частотах и т.п.). В связи с этими упрощениями схемы в различных частотных диапазонах принимают разный вид.

При составлении рабочей схемы учитываются конкретные условия работы цепи и задачи анализа. Нередко рабочая схема дополняется элементами, которые учитывают дополнительные связи в схеме: паразитные ёмкости, индуктивные связи, сопротивления соединительных проводов, сопротивления утечки и т.д.

При проектировании электронных устройств в последнее время применяют следующие основные методы анализа и расчета электронных схем: метод эквивалентных схем, метод четырехполюсника, обобщённые матричные методы контурных токов и узловых потенциалов, метод ориентированных графов.

а) Наиболее часто при анализе и расчете линейных усилительных схем пользуются методом эквивалентных схем. Он основан на замене усилительного элемента схемы (лампы, биполярного или полевого транзистора…) эквивалентной схемой (схемой замещения, моделью), состоящей из двухполюсных пассивных элементов и зависимых (управляемых) источников тока или напряжения. После этого формально задача сводится к анализу цепи с двухполюсными элементами при помощи аппарата теории электрических цепей (уравнений Кирхгофа, метода контурных токов, метода узловых потенциалов и т.д.). Пользуясь методом эквивалентных схем, можно при анализе получить выражения для расчета вторичных параметров схемы через параметры элементов эквивалентной схемы, исследовать частотные зависимости и т.п.

Этот метод удобен лишь для анализа и расчета простейших схем. С усложнением схемы применение метода ограничено громоздкостью расчетов. Кроме того, при анализе различных схем усилителей необходимо каждый раз представлять их эквивалентными схемами. И если в простых схемах этот недостаток почти не ощущается, то с усложнением схемы (особенно это касается транзисторных усилителей с цепями обратных связей) возникают трудности и при переходе от схемы к ее эквиваленту.

б) Метод четырехполюсника основан на представлении сложной усилительной схемы с двумя входными и двумя выходными зажимами в виде некоторого эквивалентного четырехполюсника. Причем сам четырехполюсник замещается некоторым соединением более простых четырехполюсников. Достоинством этого метода является то, что при его применении не требуется никаких эквивалентных схем замещения электронных ламп и транзисторов. Применяя аппарат матричной алгебры, можно значительно упростить расчеты по сравнению с методом эквивалентных схем, формализовать расчеты, что весьма важно для машинных методов анализа и расчета. Кроме того, можно также использовать заранее составленные таблицы параметров простейших (элементарных) четырехполюсников, а параметры всей схемы определить по соответствующим формулам в зависимости от способа соединения простейших четырехполюсников. Метод четырехполюсника особо широкое применение получил после появления усилительного элемента – транзистора.

Несмотря на достоинства, метод четырехполюсника имеет ряд недостатков. Основной из них - требование регулярности соединения элементарных четырехполюсников в исследуемой схеме. Нерегулярность же соединений особенно часто появляется в схемах с цепями обратных связей, вводимых сознательно в схему или возникающих за счет паразитных связей между отдельными каскадами. Правда, для анализа и расчета усилителей с нерегулярными соединениями была создана теория четырехполюсника с тремя сторонами, однако из-за сложности ее почти не применяют.

в) Пользуясь матричными методами (обобщенными) можно получать матрично-векторные параметры схемы непосредственно из рассмотрения самой схемы без ее замещения эквивалентной. Искомые токи или напряжения или вторичные параметры схемы в дальнейшем определяют через матрицы сопротивления или проводимости исследуемой схемы.

г) Метод ориентированных графов используется для адекватного представления схемы некоторой топологической структурой. Ориентированный граф состоит из множества вершин и направленных ветвей. Переход от исходной схемы к ее графу осуществляется на основе уравнений элементов схемы и зависимостей между токами и напряжениями. Интересующие функции схемы получают либо применяя формулы передачи графа, либо последовательным преобразованием графа к эквивалентной ветви.

3.2 Сущность метода эквивалентных схем

Сущность метода эквивалентных схем заключается в отображении реальных электронных цепей эквивалентными в расчетном отношении электрическими схемами на идеальных двухполюсных элементах. При этом оказывается возможным распространить на электронные цепи методы расчета электрических цепей. При таком переходе от реальной схемы к эквивалентной при отображении усилительных элементов электронных цепей (ламп, транзисторов и т.д.) их моделями возникает понятие управляемого источника тока или э.д.с. Именно введение такого зависимого (управляемого) активного элемента вместе с независимым пассивным двухполюсником и позволило в определенной степени распространить классические методы электромеханики на электронные цепи.

Последовательность операций при использовании метода эквивалентных схем для анализа электронных цепей сводится к следующему:

1) в исходной схеме усилительные элементы заменяются их эквивалентными схемами; рассматривая выводы усилительного элемента по очереди, необходимо соединить все зажимы эквивалентной схемы через соответствующие компоненты с теми же источниками напряжения или тока, что и в исходной схеме. При этом следует иметь ввиду, что внутреннее сопротивление источников питания для переменных токов принимается равным нулю, т.е. источник может рассматриваться как замкнутая цепь;

2) выбирается совокупность независимых токов и напряжений и каким-либо способом составляются уравнения эквивалентной схемы (как правило применяют метод контурных токов или метод узловых потенциалов, реже – законы Кирхгофа);

3) управляющие токи и (или) напряжения, от которых зависят источники эквивалентных схем, выражаются через токи и напряжения схемы, выбранные в качестве независимых переменных при составлении уравнений;

4) в зависимости от задачи анализа выделяются определяющие токи и напряжения, через которые определяются искомые вторичные выходные параметры схемы;

5) выражения для управляющих токов и напряжений подставляются в уравнения схемы, которые решаются относительно определяющих токов и напряжений;

6) на основании соотношений для определяющих токов и напряжений записываются выражения для искомых величин (вторичных выходных параметров).

Пример 3.1 Определить основные параметры транзисторного усилительного каскада по схеме с общей базой. Схема усилителя приведена на рис.3.1. Будем считать, что режим работы усилителя по постоянному току определен, схема работает в режиме малых сигналов; частота входного сигнала мала и параметры транзистора – действительные числа.

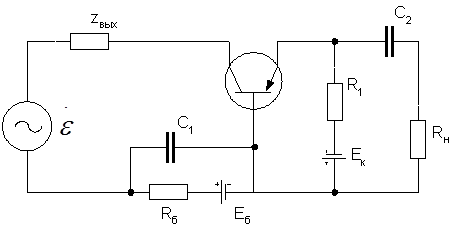
Рисунок 3.1

Считаем, что на частоте входного усиливаемого сигнала внутренние сопротивления источников питания схемы E_к и E_Б равны нулю и сопротивление емкости С₁ ничтожно мало (X₁<<R_Б). С учетом этого вычерчиваем рабочую схему усилителя (рис.3.2) – схему для переменных составляющих сигнала:

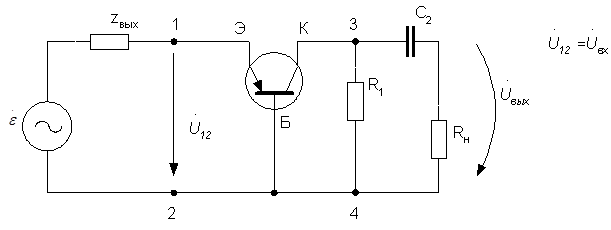
Рисунок 3.2

Для расчетов воспользуемся Т-образной физической моделью транзистора с управляемым генератором напряжений 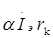(рис.3.3):

Рисунок 3.3

Схема замещения усилителя, составленная с использованием указанной модели транзистора, приведена на рис.3.4 :

Рисунок 3.4

Обозначим нагрузку усилителя относительно т.3 и 4 (R₁, R_н и С₂) как z_н. Считая, что входное напряжение усилителя 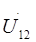известно, составим уравнения для данной схемы по методу контурных токов. Ток 1-го контура ( 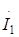) принимаем совпадающим с током 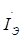. Направление тока 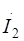принимаем в соответствии с полярностью зависимого источника .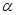

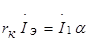
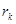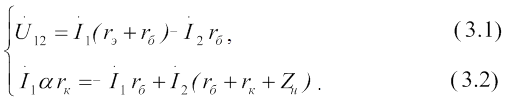
Из уравнения (3.2) получаем: .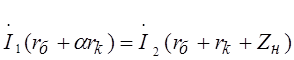

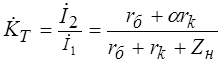- Коэффициент усиления по току транзистора в схеме усилителя.

В общем случае 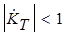, т.к. числитель меньше знаменателя. Обычно r_б<<r_k. Если можно пренебречь Z_н в сравнении с r_k, то в пределе .

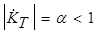Если умножить 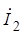на Z_н , то получим 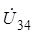, т.е. .

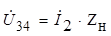Если разделить 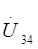на сопротивление (комплексное) цепи нагрузки, то получим ток в нагрузке, т.е.

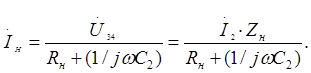
Если разделить 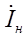на значение тока 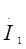, то получим коэффициент усиления усилителя по току относительно сопротивления нагрузки :

.

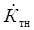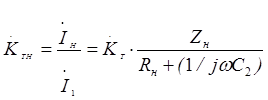Из уравнения (3.2) найдем ток 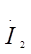и подставим в (3.1):

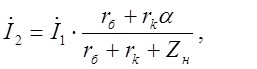
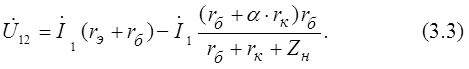
Из уравнения (3.3) можно найти входное сопротивление схемы относительно точек 1 и 2:

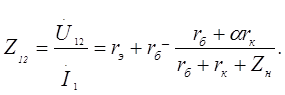(3.4)

Уравнение (3.4) позволяет оценить входное сопротивление усилителя:

r_k – для маломощных транзисторов имеет порядок нескольких кОм;

r_б – для маломощных транзисторов имеет порядок нескольких десятков Ом;

r_э – для маломощных транзисторов имеет порядок нескольких сотен Ом или нескольких кОм; Z_н – имеет порядок кОм.

Исходя из приведенного следует, что входное сопротивление усилительного каскада по схеме с общей базой мало и имеет порядок величины r_э, т.е.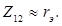

Учитывая, что

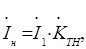
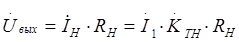и 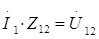, получаем формулу для расчета коэффициента усиления каскада по напряжению относительно входного напряжения:

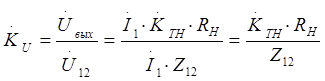(3.5)

Подставив в (3.5) найденные значения 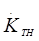и 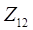, можно получить значение коэффициента усиления каскада по напряжению относительно напряжения на входе – 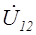. Напряжение 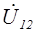можно определить, зная э.д.с. источника входного сигнала:

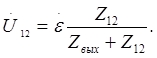
Анализ формулы (3.5) показывает, что при достаточно большом значении Z_н , т.е. больших R₁ и R_н , коэффициент усиления по напряжению может быть значительно больше 1. В области частот, где влиянием емкости С₂ можно пренебречь, 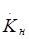- число действительное и положительное, больше 1 (т.е. данный каскад не изменяет фазу входного сигнала).

Таким образом, каскад с общей базой характеризуется:

– малым входным сопротивлением;

–коэффициентом усиления по току, меньшим 1;

–при правильном выборе сопротивлений в цепи коллектора коэффициент усиления по напряжению может быть значительно больше 1;

–каскад может обеспечить значительное усиление по мощности.

Пример 3.2. Представить эквивалентную схему (схему замещения) усилительного каскада, выполненного по схеме с общим эмиттером и охваченного отрицательной обратной связью (рис.3.5), для расчета его характеристик по переменному току; Использовать малосигнальную модель биполярного транзистора в h-параметрах.

Рисунок 3.5

Рабочая схема усилительного каскада (схема для переменных составляющих сигнала) приведена на рис.3.6 :

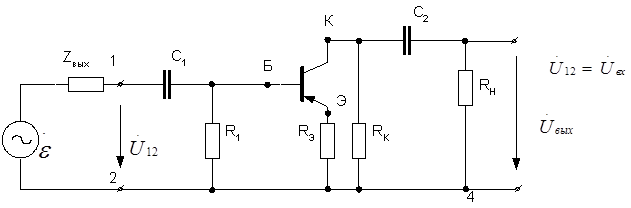
Рисунок 3.6

Малосигнальная модель биполярного транзистора в h-параметрах в схеме с общим эмиттером имеет вид:

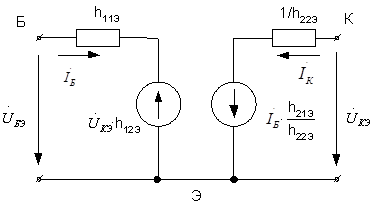
Рисунок 3.7

На основании рабочей схемы (рис.3.6), используя модель транзистора (рис.3.7), вычерчиваем эквивалентную схему усилительного каскада (рис.3.8):

Рисунок 3.8

3.3 Вторичные параметры схемы

Матрично-векторные параметры схемы (матрица схемы и задающий вектор), используемые для определения значений токов и напряжений в схеме, принято называть первичными выходными параметрами схемы.

На практике часто представляют интерес не сами токи и напряжения в схеме, а соотношения между этими величинами на входе и выходе схемы. Эти соотношения в обобщенном виде выражаются некоторыми функциями комплексной переменной p=s+jw и называются функциями схемы или вторичными выходными параметрами схемы.

Пусть к схеме с двумя входными и двумя выходными зажимами подключены, соответственно, источник энергии (или сигнала) и нагрузка. Источник входного сигнала схемы может быть представлен в виде источника напряжения Е с внутренним сопротивлением Z_u (рис.3.9а) или источника тока J c внутренней проводимостью Y_u (рис.3.9б). Нагрузка на выходе схемы может быть представлена сопротивлением Z_н (рис.1а) или проводимостью Y_н (рис. 3.9б).

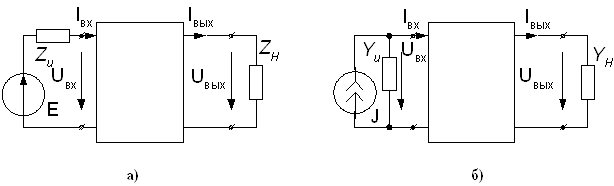Рисунок 3.9

Очевидно, что для схем, приведенных на рис.3.9, справедливо следующее:

U_вх=E - Z_u×I_вх ; I_вх=J - Y_u×U_вх ;

U_вых=Z_н×I_вых ; I_вых=Y_н×U_{вых .}

Важными вторичными параметрами схемы, характеризующими передачу сигнала (или энергии), являются следующие:

- коэффициент передачи напряжения ,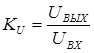

- коэффициент передачи тока ,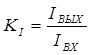

- сопротивление передачи ,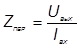

- проводимость передачи .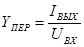

Сопротивление и проводимость передачи можно записать иначе:

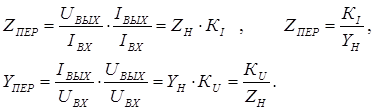
Ко вторичным выходным параметрам схемы относится также входное сопротивление:

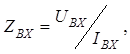
или обратная ему величина – входная проводимость:

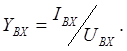
Входные сопротивление и проводимость можно выразить через другие вторичные параметры схемы:

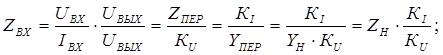
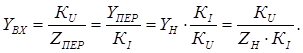
Входное сопротивление или входная проводимость характеризуют схему, как нагрузку на источник входного сигнала.

Относительно выходных зажимов схему вместе с источником входного сигнала в соответствии с теоремой об эквивалентном генераторе можно представить эквивалентным активным двухполюсником на основании опытов х.х. и к.з. При этом э.д.с. эквивалентного генератора (рис.3.10а) определяется как выходное напряжение схемы в режиме х.х., а ток эквивалентного генератора (рис.3.10б) – как ток в режиме к.з. по выходу схемы. Выходное сопротивление (проводимость) эквивалентного генератора можно рассматривать как входное сопротивление (проводимость) схемы со стороны зажимов подключения нагрузки.

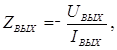
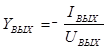
Рисунок 3.10