Матрица схемы с зависимыми источниками
Определение вторичных параметров на основе эквивалентной схемы связано с необходимостью составления уравнений (по методу контурных токов; по методу узловых потенциалов; уравнений Кирхгофа или проч.) и последующих громоздких преобразований. Этого можно избежать, если для полученной эквивалентной схемы применить методику определения вторичных параметров через матрично-векторные параметры схемы.
Действительно. Поскольку эквивалентная схема состоит из двухполюсных элементов, то система уравнений, составленная для неё то ли по методу контурных токов, то ли по методу узловых потенциалов, формально может быть записана в матричной форме:
[Q] = [W] · [X] , (3.6)
где [Q] - задающий вектор; [W] - матрица схемы; [X] - вектор состояния.
а)Если в анализе применяют метод контурных токов, то
[Е] = [Z] · [I],
где [Q]=[Е] - матрица-столбец задающих э.д.с. (задающий вектор); [W]=[Z] - матрица сопротивления схемы, [Х]=[I] - матрица-столбец контурных токов (вектор состояния).
Матрицы [Е] и [Z] образуют матрично-векторные параметры схемы. Матрица контурных токов может быть определена из решения уравнения:
[I] = [Z]-1 · [E].
б)При использовании метода узловых потенциалов уравнение (3.6) можно записать: [J] = [g] · [j];
где[J] и [g] - матрично-векторные параметры схемы; [g] - матрица проводимости схемы.
[j] = [g]-1 · [J].
Несложно показать, что в связи с наличием в схеме замещения зависимых источников вектор состояния можно представить суммой:
[Q] = [Q]¢ + [Q]¢¢,
где [Q]¢ - вектор (матрица-столбец) задающих токов или напряжений; [Q]¢¢ - вектор зависимых источников.
В свою очередь матрица схемы [W] может быть представленна суммой двух матриц:
[W] = [W]¢ + [W]¢¢, (3.7)
где [W]¢ - симметричная матрица, учитывающая только пассивные двухполюсные элементы (матрица пассивной части схемы); [W]¢¢ - матрица, связывающая вектор зависимых источников с вектором состояния схемы (матрица взаимосвязи).
Вектор (матрица) зависимых источников [Q]¢¢ и матрица взаимосвязи [W]¢¢ связаны между собой следующим матричным равенством:
[Q]¢¢ = - [W]¢¢ · [X]. (3.8)
Таким образом, матрица электронной схемы [W] может быть определенна путем суммирования матрицы пассивной части схемы [W]¢ и матрицы взаимосвязи [W]¢¢.
Порядок нахождения матрицы схемы [W] с зависимыми источниками следующий:
1) на основании эквивалентной схемы записать матрицу [W]¢ пассивной части схемы (матрицу сопротивления [Z]¢ для метода контурных токов и матрицу проводимости [g]¢ для метода узловых потенциалов);
2) записать матрицу зависимых источников схемы [Q]¢¢.
3) выразить в матрице зависимых источников [Q]¢¢ управляющие токи (напряжения) через контурные токи (узловые напряжения) эквивалентной схемы;
4) представить матрицу зависимых источников [Q]¢¢ в виде произведения некоторой матрицы [А] на вектор состояния [Х]:
[Q]¢¢ = [A] . [X];
5) записать матрицу [А] и матрицу взаимосвязи [W]¢¢ = -[A];
6) записать матрицу электронной схемы по правилу:
[W]= [W]¢+ [W]¢¢.
Как только получена матрица [W] электронной схемы, можно приступать к определению вторичных выходных параметров анализируемой схемы.
Пример 3.3 Составить матрицу сопротивления схемы усилителя на составном транзисторе – рис.3.11:
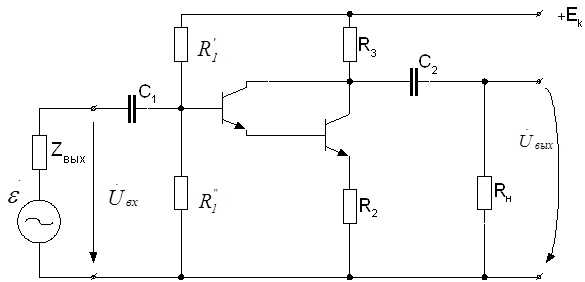
Рисунок 3.11
2) Составляем рабочую схему усилителя (схему для переменных составляющих токов и напряжений) – рис.3.12:
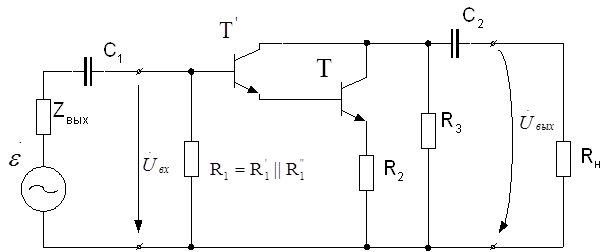
Рисунок 3.12
2) Составляем схему замещения усилителя, используя Т–образную физическую модель биполярного транзистора – рис.3.13:

Рисунок 3.13
3) Выделяем в схеме замещения (рис.3.13) независимые контуры.
Система независимых контуров, используемая при записи матрицы сопротивления схемы, должна удовлетворять следующим требованиям:
должна охватывать все ветви схемы; количество независимых контуров равно:
n = b – y + 1
где «b» – количество ветвей, «y» – количество узлов в схеме;
каждый контур должен включать хотя бы одну ветвь, которая не входит в другие контуры (это условие для сложных схем не является обязательным);
входное напряжение (ток) должно входить только в один независимый контур – входной контур (номер «а»); выходное напряжение тоже должно входить только в один – выходной контур (номер «b»); эти контуры образуют внешние контуры схемы.
В анализируемой схеме y=5, b=9, значит n=5. Входной контур – а=1; выходной контур – b=5.
3) Записываем матрицу сопротивления пассивной части схемы – [Z]', она не учитывает наличие в схеме замещения зависимых источников; размер этой матрицы n´n (5´5):
| [Z]¢= | ||||||
| XC1+R1 | -R1 | 0 | 0 | 0 | ||
| -R1 | R1+rб¢+rэ¢+ +rб +rэ +R2 | -R2- rэ - - rб - rэ¢ | -R2- rэ | 0 | ||
| 0 | -R2- rэ - - rб - rэ¢ | R2+rб +rэ + +rk¢+ rэ¢+R3 | R2+R3+rэ | -R3 | ||
| 0 | -R2- rэ | R2+R3+rэ | R2+rэ + +rк +R3 | -R3 | ||
| 0 | 0 | -R3 | -R3 | R3+XC2 |
Примечание: внутреннее сопротивление источника входного сигнала схемы Zвых и сопротивление нагрузки усилителя Rн в матрицу [Z] не вносить!!!
5) Записываем матрицу-столбец зависимых источников [Е]¢¢: в нее входят э.д.с. зависимых источников и она имеет размер 5´1:
| [E]¢¢= | 0 | |
| 0 | ||
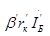
| ||

| ||
| 0 |
6) Выражаем управляющие величины (токи) зависимых источников через контурные токи , составляя таблицу зависимых источников:
| Управляемый источник | Управляющий параметр | Управляющая величина источника |
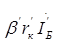
| 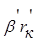
| 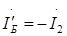
|
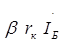
| 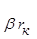
| 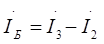
|
7) Представляем матрицу–столбец [Е]¢¢ в виде произведения [А] ´ [ 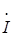 ]¢, где [A] – некоторая матрица размером 5´5; [
]¢, где [A] – некоторая матрица размером 5´5; [ 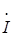 ] – матрица–столбец контурных токов (размер 5´1):
] – матрица–столбец контурных токов (размер 5´1):
| 0 | 0 | 0 | 0 | 0 | 0 | 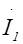
| ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 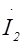
| ||||
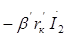
| = 3 | 0 | 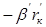
| 0 | 0 | 0 | ´ | 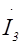
| ||
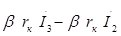
| 0 | 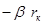
| 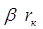
| 0 | 0 | 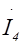
| ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 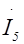
| ||||
| [E]¢¢ | [A] | [I] |
8) Записываем матрицу взаимосвязи [Z]¢¢, используя правило [Z]¢¢=– [A]. Для этого надо изменить знаки элементов матрицы [A] на противоположные.
9) Записываем полную матрицу сопротивления анализируемой схемы, суммируя соответствующие элементы матриц [Z]¢ и [Z]¢¢:
[Z] = [Z]¢ + [Z]¢¢ .
Из рассмотренного примера видно, что матрица взаимосвязи состоит из управляющих параметров зависимых источников. В данном случае управляющим параметром 1-го зависимого источника является 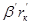 , а управляющим параметром 2-го источника -
, а управляющим параметром 2-го источника - 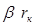 . Управляющей величиной 1-го источника является ток
. Управляющей величиной 1-го источника является ток 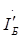 , а управляющей величиной 2-го источника -
, а управляющей величиной 2-го источника - 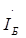 .Из примера видна закономерность, по которой управляющие параметры вписывают в матрицу сопротивления схемы. Положение параметра в матрице определяется связью зависимого источника и управляющей величины источниками с контурами схемы.
.Из примера видна закономерность, по которой управляющие параметры вписывают в матрицу сопротивления схемы. Положение параметра в матрице определяется связью зависимого источника и управляющей величины источниками с контурами схемы.
Управляющий параметр вписывается в матрицу на пересечении некоторых строк и столбцов по следующему правилу:
а) номера строк соответствуют номерам контуров, в которые входит зависимый источник, а номера столбцов – контурных токов, через которые выражаются управляющие величины (токи);
б) если зависимый источник и контур, в который он входит, совпадают по направлению, а управляющая величина (ток) также совпадает по направлению со связанным с ней контурным током, то управляющий параметр вписывается в соответствующую клетку матрицы со знаком “-”; при изменении одного направления знак меняется на противоположный; правило знаков можно представить в виде таблицы:
| Направление зависимого источника относительно контурного тока, определяющего номер строки | Направление управляющего тока зависимого источника относительно контурного тока, определяющего номер столбца | Знак управляющего параметра в соответствующей клетке матрицы |
| совпадает | совпадает | – |
| не совпадает | + | |
| не совпадает | не совпадает | – |
| совпадает | + |
Пример 3.4 Записать матрицу проводимости схемы двухкаскадного усилителя с отрицательной обратной связью, приведенной на рис.3.14

Рисунок 3.14
1) Составляем рабочую схему усилителя (схему для переменных составляющих токов и напряжений) для диапазона частот, где реактивным сопротивлением емкостей С1,С2,С3 и С4 можно пренебречь – рис.3.15

Рисунок 3.15
2) Составляем малосигнальную схему замещения усилителя, используя линейную модель полевого транзистора с источником тока – рис.3.17 (модель ПТ приведена на рис.3.16).

Рисунок 3.16

Рисунок 3.17
3) В схеме замещения номеруем все узлы цифрами 0,1,2…n. Выделяем входной узел (его номер “а”) и выходной узел (номер “b”). В анализируемой схеме а=1, b=4.
Составляем матрицу проводимости пассивной части схемы, не учитывающую наличие в схеме зависимых источников. Ее размер n´n (в анализируемой схеме - 4´4):
| [Y]¢= | g1 | ||||
| Gi¢ + g24 | - Gi¢ | ||||
| - Gi¢ | g3+ Gi¢ + g6 | -g6 | 3 | ||
| -g6 | g5+ Gi2 + g6 | 4 |
Примечание: проводимость источника входного сигнала схемы gвых и проводимость нагрузки gн в матрицу [Y] не вносить!!!
4) Составляем таблицу зависимых источников анализируемой схемы
| Зависимый источник | Управляющий параметр зависимого источника | Управляющая величина (напряжение) источника |
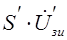
| 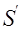
| 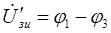
|
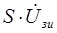
| 
| 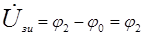
|
5) Записываем матрицу взаимосвязи [Y]¢¢. Она, как и матрица [Y]¢, имеет размер 4´4; содержит матрица [Y]¢¢ управляющие параметры зависимых источников, которые вписывают в клетки матрицы на пересечении некоторых строк и столбцов, используя следующие правила:
а) номера строк соответствуют номерам узлов, к которым присоединен зависимый источник;
б) номера столбцов соответствуют номерам узлов, через потенциалы которых определяется управляющая величина (напряжение) источника – см. табл. зависимых источников;
в) знаки управляющих параметров в соответствующих клетках матрицы определяют согласно приведенной ниже таблице
| Направление зависимого источника относительно узла, определяющего номер строки | Направление управляющего напряжения относительно узла, определяющего номер столбца | Знак управляющего параметра в соответствующей клетке матрицы |
| от узла | от узла | + |
| к узлу | – | |
| к узлу | к узлу | + |
| от узла | – |
Для анализируемой схемы матрица [Y]¢¢ имеет вид:
| [Y]¢¢= | |||||
| +S¢ | – S¢ | ||||
| – S¢ | +S¢ | ||||
| +S |
6) Полная матрица проводимости схемы равна сумме матриц [Y]¢ и [Y]¢¢:
[Y] = [Y]¢ + [Y]¢¢ .
Примечание: суммируя матрицы [Y]¢ и [Y]¢¢, следует выполнить алгебраическое суммирование элементов соответствующих клеток этих матриц.
3.5 Связь вторичных выходных параметров с
матрицей сопротивления (проводимости) схемы
Пусть для анализируемой схемы составлена схема замещения, содержащая в своём составе и зависимые источники. При составлении уравнений для контурных токов условимся выбирать независимые контуры таким образом, чтобы каждое из внешних напряжений схемы - 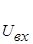 и -
и - 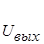 - входило только в один контур. Таким образом будем иметь два внешних контура – входной и выходной. Пусть направление обхода этих контуров выбрано одинаковым – например, по часовой стрелке (рис.3.18). Обозначим номер входного контура “a”, а выходного - “b”. На выбор остальных контуров схемы ограничений не накладываем, кроме требований их взаимной независимости.
- входило только в один контур. Таким образом будем иметь два внешних контура – входной и выходной. Пусть направление обхода этих контуров выбрано одинаковым – например, по часовой стрелке (рис.3.18). Обозначим номер входного контура “a”, а выходного - “b”. На выбор остальных контуров схемы ограничений не накладываем, кроме требований их взаимной независимости.
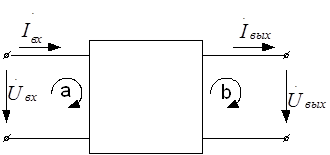
Рисунок 3.18
В выбранной системе независимых контуров внешние токи 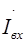 и
и 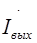 соответствуют контурным токам
соответствуют контурным токам 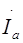 и
и 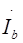 внешних контуров. Для данной схемы может быть составлена система алгебраических уравнений, решение которой для внешних токов можно записать в виде:
внешних контуров. Для данной схемы может быть составлена система алгебраических уравнений, решение которой для внешних токов можно записать в виде:
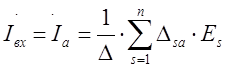 ,
,

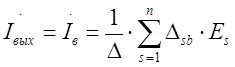 .
.
где D – определитель матрицы сопротивления схемы, записанной в выбранной системе контуров; S – номер независимого контура схемы; 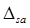 = Msа·(-1)s+а – алгебраическое дополнение матрицы сопротивления схемы; Msа – минор элемента Zsа матрицы сопротивления схемы (его получают из определителя Δ путем вычеркивания S-й строки и а-го столбца).
= Msа·(-1)s+а – алгебраическое дополнение матрицы сопротивления схемы; Msа – минор элемента Zsа матрицы сопротивления схемы (его получают из определителя Δ путем вычеркивания S-й строки и а-го столбца).
Внутри схемы отсутствуют независимые источники сигналов, поэтому задающие э.д.с. всех внутренних контуров равны нулю, т.е. Es = 0 при S 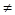 а и S
а и S 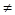 b. Задающие э.д.с. внешних контуров определяются внешними напряжениями схемы:
b. Задающие э.д.с. внешних контуров определяются внешними напряжениями схемы: 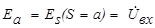 и
и 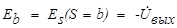 . С учетом этого уравнения для внешних токов схемы принимают вид:
. С учетом этого уравнения для внешних токов схемы принимают вид:
 , (3.9)
, (3.9)
 . (3.10)
. (3.10)
Решив уравнения (3.9) и (3.10) относительно внешних напряжений схемы, получим:
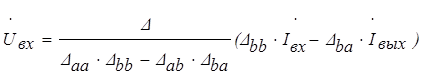 ,
,

Воспользуемся известной из матричной алгебры зависимостью
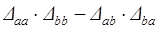 =
= 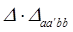 , (3.11)
, (3.11)
где 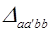 - двойное алгебраическое дополнение матрицы сопротивления схемы [Z], получающееся путем вычеркивания из определителя матрицы двух строк и двух столбцов с номерами “a” и “b”.
- двойное алгебраическое дополнение матрицы сопротивления схемы [Z], получающееся путем вычеркивания из определителя матрицы двух строк и двух столбцов с номерами “a” и “b”.
Тогда получим:
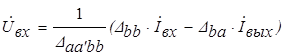 , (3.12)
, (3.12)
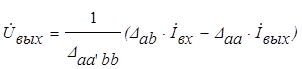 . (3.13)
. (3.13)
Уравнения (3.9)…(3.13) позволяют выразить вторичные выходные параметры схемы (приводящейся к виду четырехполюсника) через определитель и алгебраические дополнения матрицы сопротивления схемы (методика её получения рассмотрена ранее).
Подставим значения 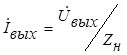 в уравнение (3.10):
в уравнение (3.10):
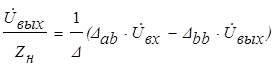 .
.
Разделяя 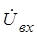 и
и 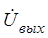 из последнего получаем:
из последнего получаем:
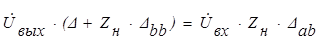 ,
,
откуда
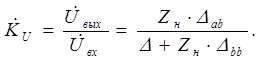 . (3.14)
. (3.14)
При к.з. на выходе (Zн=0), 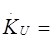 0.
0.
При х.х. на выходе (Zн®¥), из (3.14) получаем:
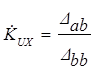 . (3.15)
. (3.15)
Подставим значение  в (3.13). После несложных преобразований получаем:
в (3.13). После несложных преобразований получаем:
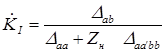 . (3.16)
. (3.16)
При х.х. на выходе схемы 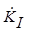 =0, а при к.з. (Zн=0)
=0, а при к.з. (Zн=0)
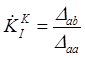 . (3.17)
. (3.17)
Учитывая, что 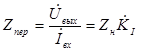 , получим
, получим
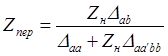 . (3.18)
. (3.18)
Аналогично
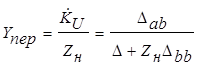 . (3.19)
. (3.19)
Для определения входного сопротивления можно воспользоваться ранее полученной зависимостью
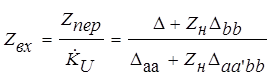 . (3.20)
. (3.20)
Входное сопротивление при к.з. выхода схемы будет (Zн=0):
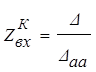 ,
,
а при х.х. на выходе (Zн®¥):
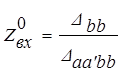 .
.
Следует отметить, что матрица сопротивления, которую мы использовали выше при расчете вторичных параметров схемы, не включает в себя выходное сопротивление Zи источника входного сигнала и сопротивление нагрузки Zн. Поэтому, если при анализе схемы необходимо определить полный коэффициент усиления по напряжению (относительно э.д.с. источника входного сигнала) 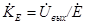 , в отличие от коэффициента
, в отличие от коэффициента 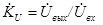 , то необходимо учитывать и коэффициент передачи по напряжению входной цепи:
, то необходимо учитывать и коэффициент передачи по напряжению входной цепи:
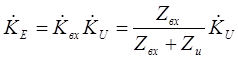 ,
,
Далее в таблице приведены некоторые выражения для расчета вторичных выходных параметров анализируемой схемы используя определитель Δ и алгебраические дополнения Δij матрицы сопротивления [Z] (проводимости – [Y]) схемы. Более полная таблица приведена в кн. “Сигорский В.П., Петренко А.Н. Основы теории электронных схем. Киев, 1967.”
| Вторичный параметр | Обозначение | Формула | |
| [Z] | [Y] | ||
| Коэффициент передачи тока | 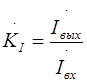
| 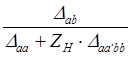
| 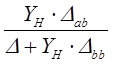
|
| Коэффициент передачи напряжения | 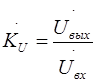
| 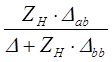
| 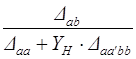
|
| Входное сопротивление |  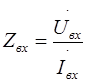
| 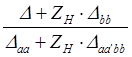
| |
| Входная проводимость | 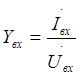
| 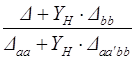
| |
| Сопротивление передачи |  
| 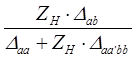
| 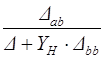
|
| Проводимость передачи | 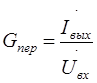
| 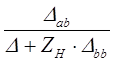
| 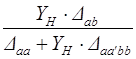
|
3.6 Условия стационарности (самовозбуждения)
генератора
Хотя генераторы колебаний являются нелинейными системами, условия стационарности (условия возбуждения) могут быть найдены на основании линейной теории. Напряжения и токи в установившемся режиме при этом считаются гармоническими, не зависящими от амплитуды. Поэтому при анализе применим символический метод.
Пусть имеется некоторая электрическая схема, матрица W которой известна. Решение матричного уравнения [Q]=[W].[X] этой схемы относительно искомого вектора состояния [X] имеет вид:
[X]=[W]-1.[Q].
Для того, чтобы схема была генератором гармонических колебаний, компоненты вектора [X] должны быть гармоническими функциями времени с постоянными амплитудами, отличными от нуля, даже когда компоненты задающего вектора [Q] нулевые. Как известно, это возможно при условии
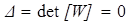 .
.
Составив матрицу [W] в символической форме, можно записать ее определитель в виде комплексного выражения:
D = A(ω) + jB(ω) = Re(D) + jIm(D) .
Условие стационарности имеет вид:
A(w) = 0 , B(w) = 0.
Совместное решение этих равенств позволяет определить частоту w0, которая устанавливается в схеме, а также установить связь между параметрами элементов схемы для того, чтобы последняя была способна генерировать колебания этой частоты. При таком рассмотрении элементы схемы предполагаются линейными и в условия стационарности не входят амплитуды токов и напряжений. Это значит, что теоретически возможны любые значения амплитуд, определяемые начальными условиями.
В действительности существенным для генераторов является наличие нелинейных элементов, ограничивающих значения амплитуд токов и напряжений. Однако определение последних выходит за рамки линейной теории.
Таким образом, приведенные уравнения A(w) = 0 и B(w) = 0 могут быть положены в основу линейной теории возбуждения генератора гармонических колебаний. Их получение существенно упрощается, если воспользоваться методикой записи матрицы схемы.
Дата добавления: 2016-01-03; просмотров: 2727;
