Глава II. Дискретность электронных и атомных состояний. 3 страница

Рассмотрим теперь предельные случаи зависимости 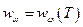, которые были объяснены теоретически.

1. 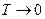. Рэлей и Джинс предположили, что если излучение тепловое, то на каждую степень свободы по классической теореме о равнораспределении энергии по степеням свободы приходится энергия 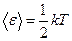. У гармонического осциллятора средняя кинетическая энергия равна средней потенциальной, поэтому его средняя энергия равна 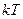. Поскольку в условиях термодинамического равновесия в полную статистическую систему входят излучение в полости и осцилляторы стенок полости, это означает, что средняя энергия, приходящаяся на одну моду колебаний в плоскости, 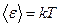. Тогда объёмная спектральная плотность энергии будет равна: 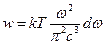, или . 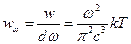Данная формула распределения плотности энергии теплового излучения по спектру даёт достаточно хорошее согласие с экспериментом на малых частотах. Однако простой анализ показывает, что при 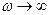, 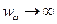. Данное явление абсолютно не согласуется с опытом. Причём при больших 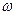рассчитанная частота оказывается значительно больше опытной. Этот факт получил название ультрафиолетовой катастрофы. Основная ошибка здесь заключается в том, что при выводе формулы не учитывались квантовые свойства системы.

2. 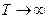. В. Вин предположил, что каждая мода колебаний является носителем энергии 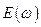, но не все моды данной частоты в полости возбуждены. Относительное число возбуждённых мод определяется распределением Больцмана: 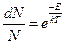. Отсюда средняя энергия, приходящаяся на моды с частотой 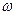, , 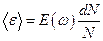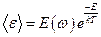. При этом, энергия любого типа колебаний пропорциональна частоте: 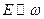. С введением постоянной Планка, стало возможным записать: 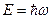, а 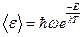. Тогда для объёмной спектральной плотности энергии мы можем записать: 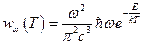. Полученное соотношение называют формулой Вина. Она описывает зависимость 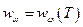лишь при больших частотах.

В 1900 г. Максом Планком была получена формула, описывающая зависимость 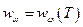на всём диапазоне частот. Он исходил из предположения, что осциллятор не может обладать любой энергией, а лишь дискретным набором энергий, пропорциональных некоторой минимальной энергии 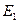. Он поставил в соответствие каждой моде свой гармонический осциллятор: 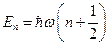, где 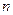– номер энергетического уровня. Слагаемое 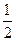получается с учётом энергии вакуума. Число мод в полости 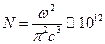. С другой стороны, 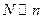. Тогда 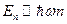. Обозначим через 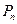вероятность того, что при температуре 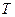осциллятор будет находиться на 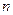– ом энергетическом уровне. Так как мы имеем дело с тепловым излучением, то вероятность 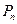будет описываться распределением Больцмана: 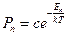. Здесь 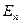– энергия на 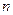– ом энергетическом уровне. Тогда среднее значение на всех энергетических уровнях будет определяться следующим выражением: 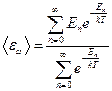. Мы получили в знаменателе сходящуюся геометрическую прогрессию с параметрам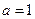и и 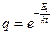. Как известно, сумма бесконечно убывающей геометрической прогрессии равна: 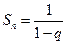. Таким образом, 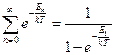. Возвращаясь к указанному выше выражению для энергии, можно записать: 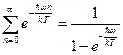. Продифференцируем последнее выражение по 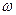: 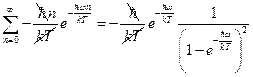, 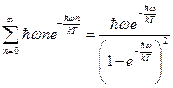. Тогда средняя энергия, приходящаяся на один осциллятор, с учётом последнего уравнения будет равна: 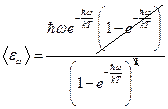. Домножим полученное соотношение на 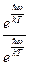. Получим: 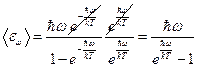. И окончательно, 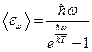. Найдём теперь объёмную спектральную плотность энергии, с помощью выражения: 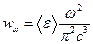. 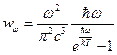(3). Полученная формула называется формулой Планка и описывает излучение абсолютно чёрного тела во всём диапазоне частот. В пределах пр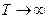и и 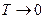, данная формула сводится к формулам Вина и Рэлея – Джинса. Найдём полную объёмную плотность излучения. Для этого необходимо взять интеграл от (3) по всем частотам: 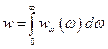. Подставляя в данный интеграл полученное выше значение для объёмной спектральной плотности энергии, получим:

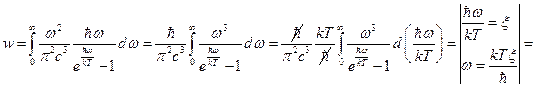
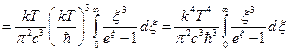. Полученный интеграл затабулирован и имеет значение: 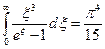. Таким образом, 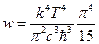. Введём обозначение 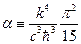. Данная величина является

константой, так как из констант составлена. Итак, для объёмной плотности излучения можно записать: 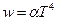. Вспоминая второй закон Кирхгофа 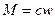, получим: 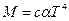, где 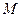– энергетическая светимость или 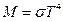. Полученное уравнение определяет энергетическую светимость абсолютно чёрного тела: энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его температуры. Данный закон называется законом Стефана – Больцмана. Константа 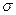в этом уравнении равна: 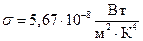. Найдём теперь максимальную спектральную плотность энергии излучения в единицу длин волн. Для этого в выражении (3) перейдём от частоты 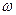к длине волны 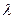: 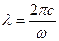, 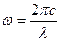(4). По определению 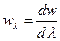, а 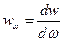то есть 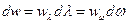; 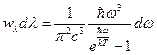. Подставляя в последнее соотношение (4), получим: 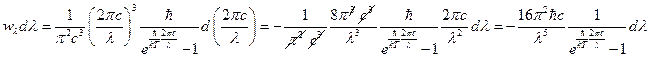. Сравнивая начало и конец данного выражения, получим: 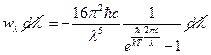, 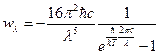. Так как энергия излучения не может быть отрицательной, мы должны взять модуль этого выражения. В итоге получим: 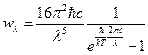. Исследуем его на экстремум. 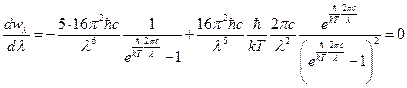. Сократим константы 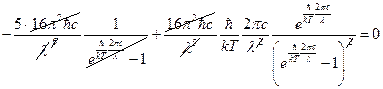, 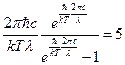. Введём для удобства обозначение: 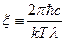, тогда последнее выражение перепишется в виде: 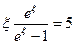, , 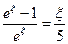, 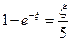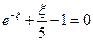. Мы получили итерационное уравнение относительно переменной 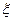. Решая его, найдём эту переменную, а потом из ней выразим и 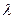. . 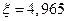Тогда рассматривая выражение для 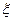: 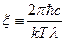, нетрудно заметить, что часть его есть некоторая константа: 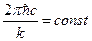. Поэтому мы можем получить уравнение, связывающее 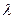и 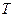: 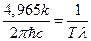или, записывая это выражение в общепринятой форме, имеем: 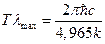. Константа, стоящая в этом выражении справа равна: 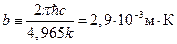. Итак, мы получили закон смещения Вина: произведение длины волны, соответствующей максимуму спектральной плотности энергии излучения абсолютно чёрного тела на температуру излучения есть величина постоянная и независящая от рода излучающего тела: .

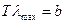Данная формула имеет большое значение в астрофизике при определении температуры звёзд. Можно, например, посчитать, чему равна длина волны, соответствующая максимуму спектральной плотности энергии излучения для нашего Солнца. Известно, что температура его поверхности в среднем равна примерно 6000 К. Тогда по формуле смещения Вина получим, что .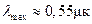

§ 2.2.Экспериментальное подтверждение дискретной природы энергетических уровней атомов и молекул.

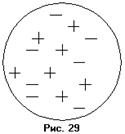
Любое излучение электромагнитных волн осуществляется телами. Если излучение дискретно, то тело должно переходить с одного дискретного уровня на другой. Опыты Франка и Герца дали прямое доказательство дискретности атомных состояний. Если состояние атомных систем дискретно, а кинетическую энергию свободных электронов мы можем менять непрерывно, то при взаимодействии электронов с атомами, атомы могут поглощать энергию лишь строго определёнными порциями. В ходе опыта использовалась вакуумная лампа (см. рис. 29). В ней находились накаливающийся катод, анод и две сетки, которые соединялись между собой. На сетку подавался ускоряющий пот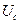енциал . 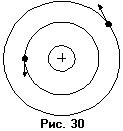Изменением его можно было плавно изменять кинетическую энергию электронов. На другую сетку подавался задерживающий потенциал 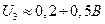. Электроны, ускоренные между сеткой и катодом, попадали в свободное от полей пространство. Наблюдалась ВАХ, представленная на рисунке 30. Если теперь наполнить трубку парами (например, ртути) при пониженном давлении, в пространстве между сетками будут происходить столкновения электронов с атомами ртути. Те, что не потеряли энергию в результате подобных столкновений, достигнут анода. Те же, что энергию потеряли, анода не достигают. Анодный ток убывает. ВАХ лампы в этом случае представлена на рисунке 31. Качественно её можно объяснить следующим образом. Когда энергия электрона меньше разности энергий между энергетическими уровнями ртути, то оно не отдаёт энергию атому при 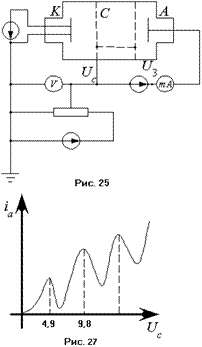столкновении. С увеличением ускоряющей разности потенциалов энергия электронов также возрастает. Когда разность потенциалов достигает 4,9 эВ., электроны при неупругом столкновении с атомами ртути вблизи сетки отдадут им всю свою энергию и уже не смогут преодолеть запирающей разности потенциалов. Следовательно, на анод могут попасть лишь

электроны не испытавшие неупругого столкновения, и поэтому при разности потенциалов 4,9В. сила тока начинает уменьшаться. Когда разность потенциалов достигает такого значения, что достаточное число электронов после неупругого столкновения смогут приобрести энергию, необходимую для преодоления задерживающего потенциала, начинается новый рост силы тока. При достижении разности потенциалов 9,8 В., электрон после одного неупругого столкновения приходит к сетке с энергией 4,9 эВ., достаточной для второго неупругого столкновения. При втором неупругом столкновении электрон теряет всю свою энергию и не достигает анода. Поэтому сила тока начинает уменьшаться (второй максимум на ВАХ). Последующие максимумы объясняются аналогично. Из опыта следует, что разница в энергии основного состояния атома ртути и ближайшего возбуждённого состояния равна 4,9 эВ., что и доказывает дискретность состояний атомных систем.

Отношение энергии возбуждения атома к заряду электрона называется потенциалом ионизации: 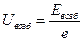. Первый потенциал возбуждения соответствует переходу атома с уровня с наименьшей энергией на последующий уровень.

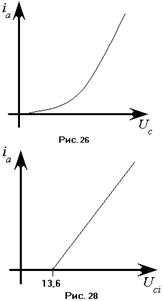
Ионизацией называется процесс отрыва электрона от атома. Для определения потенциала ионизации также используют установку, изображённую на рисунке 29. Потенциал ионизации определяется по формул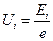е , где 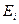– работа выхода электрона из атома. Для атома водорода ВАХ этого процесса имеет вид, представленный на рисунке 32. Здесь измеряется ток, создаваемый положительными ионами. Величина 13,6 В. называется потенциалом насыщения.

§ 2.3.Спектры испускания и поглощения атомов.

Все спектры (испускания, поглощения) делятся на линейчатые, полосатые и сплошные. Чем проще структура вещества, тем разрежённей его спектр. С другой стороны, чем меньше электронов содержит вещество, тем проще его спектр. Линейчатые спектры характерны для атомов определённых веществ. Полосатые спектры дают молекулы газа в разряженном состоянии. Сплошным спектром обладает газ при высокой температуре или жидкость, а также твёрдые тела.

Во второй половине 19 века были проведены многочисленные и тщательные исследования спектров излучения. Исследователи обнаружили, что спектральные линии объединяются в серии. Серией называется группа спектральных линий, соответствующая переходу атома с одного и того же энергетического уровня на какой-либо другой (для спектра испускания) либо в одно и то же энергетическое состояние (для спектра поглощения). Первая спектральная серия для атома водорода была обнаружена Бальмером в 1885 г. и получила его имя. Изучая спектр атома водорода в видимой области, Бальмер получил формулу: , где 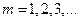. Впоследствии были открыты и остальные серии для атома водорода:

1. Серия Лаймана. 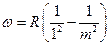. Ультрофиалетовая область.

2. Серия Пашена. 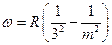. Инфракрасная область.

3. Серия Брэкета. 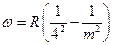. Инфракрасная область.

4. Серия Пфунда. 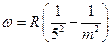. Инфракрасная область.

Расстояния между спектральными линиями с увеличением числа 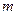становится всё меньше и меньше. Это утверждение очевидно следует из приведённых выше формул. Обобщая, можно записать закон построения спектральных линий для атома водорода для всех серий: 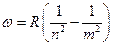, где 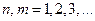. Причём 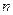определяет номер спектральной серии. 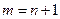для спектра испускания; 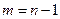для спектра поглощения.

Введём понятие спектрального терма: 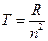. Таким образом, частота любой спектральной линии определяется линейной комбинацией термов 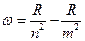(1). Этот принцип называют комбинационным принципом Ритца: всё многообразие спектральных линий одноэлектронного атома является комбинацией спектральных термов. Как будет постулировано в дальнейшем, частота излучённой электромагнитной волны при переходе атома с одного энергетического уровня на другой определяется формулой: 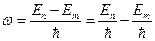(2), где 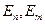– энергии соответствующих энергетических уровней. Таким образом, сравнение формул (1) и (2) даёт, что физический смысл терм есть отношение энергии уровня к постоянной Планка. Следует отметить, что принцип Ритца справедлив только для определённого ряда атомов, у которых на внешней оболочке либо один электрон, либо одного нет. Это – так называемые водородоподобные атомы. К их числу принадлежат ионы, щелочные металлы и т. д. В данном случае справедлива формула: 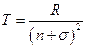, где 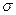– некоторая константа, в каждом случае своя.

В спектре атома других линий быть не может, тем не менее, не все линии, определяемые комбинационным принципом Ритца, обязательно присутствуют в спектре, так как не нулевой вероятностью обладают лишь переходы, удовлетворяющие правилам отбора.

§ 2.4.Ядерная модель атома.

Исторически существовало две признанных модели атома: модель Томпсона и модель Резерфорда.

По модели Томпсона (рис. 35) атом представлял собой непрерывно распределённый в пространстве положительный заряд, в который были вкраплены отдельные отрицательные заряды. Электроны взаимодействуют с элементами положительно заряженной среды атома по закону Кулона. При отклонении электрона от положения равновесия, возникают силы, которые стремятся возвратить его в положение равновесия. Благодаря этому возникают колебания электрона. Колебания электронов обуславливают излучение атомов.

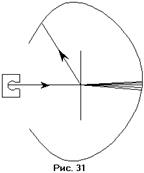Вторая модель, модель Резерфорда (рис.36), приписывала атому строение, аналогичное строению Солнечной системы: в центре находится положительно заряженное ядро, вокруг которого, подобно планетам, движутся электроны, удерживаемые у ядра силами кулоновского притяжения. Спор между двумя этими теориями разрешил эксперимент, поставленный Резерфордом. Резерфорд изучал движение тяжёлых положительно заряженных частиц в поле, создаваемом атомом. Схема использовавшейся установки приведена на рисунке 31. Узкий пучок 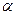– частиц из источника излучения падала на тонкую золотую фольгу. За фольгой находилась поверхность, покрытая веществом, способным сцинтиллировать, например, 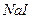. 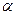– частицы пролетали сквозь фольгу и падали на сцинтиллятор. Сцинтиллятор на короткое время начинал светиться в точке падения 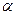– частиц. За этими вспышками как раз и наблюдали. Если бы взаимодействия частиц с веществом не было, то вспышки наблюдались бы все в одном и том же месте. Тем не менее, большинство частиц отклонялись от направления своего первоначального движения на 3°-5°, и что ещё более интересно, приблизительно одна из 6000 – 8000 частиц отклонялась от первоначального направления движения на угол более 90°. В то же время не было частиц, которые притягивались бы. Это навело Резерфорда на мысль, что в атоме должен находиться мощный силовой центр, который заставляет отклоняться частицы на большие углы, причём, так как заряд 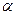– частицы считался положительным, этот силовой центр также должен быть положительным. Редкость отскакивания частицы на угол более 90° говорила о том, что центр должен быть точечным. Итак, по Резерфорду получалось, что в центре атома существует нечто, обладающее большой массой и имеющее малые размеры и положительный заряд. Изучая движение частиц сквозь фольгу, Резерфорд получил соотношение, связывающее угол рассеяния частицы с прицельным параметром 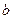. Прицельным параметром 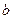называется расстояние наименьшего сближения частиц, при отсутствии 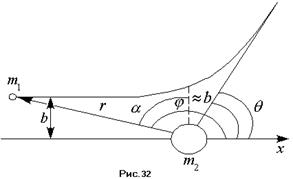взаимодействия между ними (см. рис. 32). Получим это соотношение. Пусть на положительно заряженную частицу массой 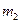и зарядом 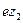налетает положительно же заряженная частица массой 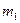, движущаяся со скоростью 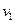и имеющая заряд 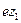, причём 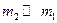. Тогда при движении частицы в поле центральных сил, должна сохраняться энергия системы и момент импульса частиц. Запишем эти законы: 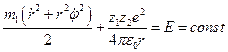(1) – закон сохранения энергии1. 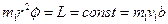– момент импульса для первой частицы. Из последнего выражения можно записать: 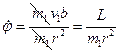(2); 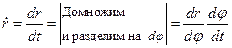. Осуществим замену переменных: 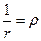. Тогда 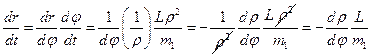. Подставляя полученное выражение в (1), переходя к переменной 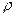, получим: 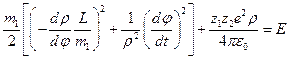. Раскроем скобки. Тогда 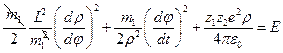. Умножим слева и справа это выражение на 2 и перенесём вправо слагаемое, характеризующее потенциальную энергию взаимодействия: 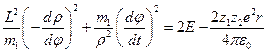. Совершим некоторые очевидные преобразования: 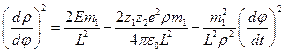. Возвращаясь к формуле (2), и подставляя ей в данное выражение, получим: 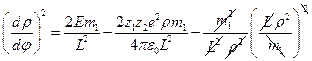, или 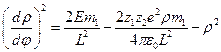. Продифференцируем теперь по 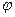: 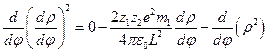; 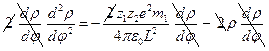, 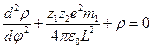. Введём следующее обозначение: 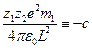. Тогда рабочее соотношение примет вид: 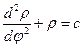. Решением данного уравнения, как нетрудно убедиться, будет 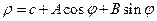(3) . чтобы найти неизвестную константу 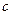, прибегнем к следующему приёму. Рассмотрим случай, когда частицы находятся друг от друга бесконечно далеко. Тогда можно записать следующее соотношение: при 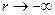, 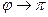. Тогда, подставляя данное допущение в уравнение (3), получим: 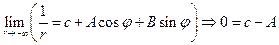; 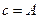. Таким образом, мы получили всего две неизвестных константы и два граничных условия. Из рисунка 32 следует очевидное равенство: 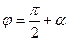, 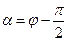. Из рисунка 32 также следует, что 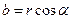, а с учётом последнего выражения 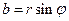. Отсюда 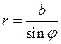. Тогда, с помощью этого выражения, а также уравнения (3) мы получим при 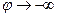: 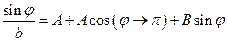. 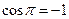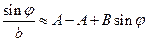Так как , то или 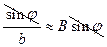, 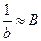. Таким образом, возвращаясь к уравнению (3), получим: 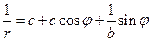Разделим полученное выражение на 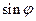: 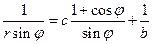. Разложим синусы и косинусы по формулам половинного аргумента и сократим подобные множители: 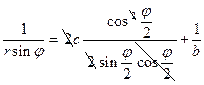; 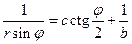. Рассмотрим теперь другое предельное значение угла 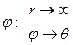. Тогда 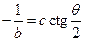и . 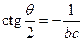Подставляя сюда значение постоянной 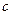, получим: 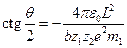. Возведём в квадрат закон сохранения импульса; полученный результат подставим в рабочую формулу: 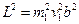, 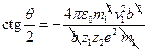; 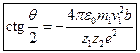(4). Последняя формула была получена Резерфордом и связывает угол рассеяния частицы с прицельным параметром 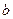. Оставалось только проверить эту формулу. В опыте Резерфорд имел дело не с одной частицей, а с большим их числом. Частицы двигались под некоторыми углами, то есть имел место некоторый разброс углов. Частицы рассеивались на различных атомах и после рассеяния приобретали некоторые импульсы, значения которых также претерпевали некоторый разброс. Для того чтобы описать данный процесс, немыслимо пытаться рассчитывать траекторию движения каждой частицы. Полученная система уравнений будет слишком громоздка и практически неразрешима. В данном случае уместно прибегнуть к теории вероятностей. Введём понятие дифференциального поперечного сечения рассеяния 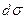в угол между 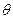и 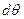. Так будем называть отношение числа частиц 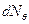, рассеянных в единицу времени в угол 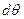к полному потоку частиц 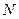: 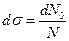. Здесь 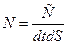, где 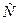– полное число частиц. 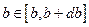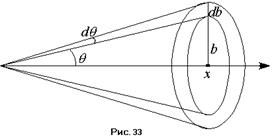Все частицы, для которых , будут рассеиваться в угол 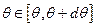. Число частиц, прицельный параметр которых заключён в этом интервале, будет равно числу частиц, падающих на кольцо шириной 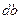и радиусом внутренней окружности 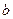: 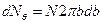. Тогда 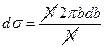, 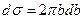. Нам не важен здесь знак 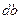, поэтому в дальнейшем будем рассматривать лишь его модуль. Воспользуемся теперь полученной нами формулой (4) для нахождения 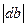: 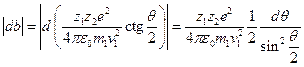. Подставляя полученное выражение в уравнение для 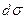, получим 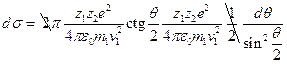, 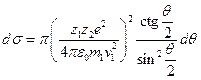. Последняя формула называется формулой Резерфорда. Перейдём теперь от плоского угла 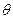к телесному 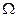. Известно, что они связаны соотношением 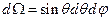в сферической системе координат. Тогда если угол 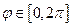, 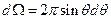. Из последней формулы выразим 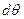и подставим его в формулу Резерфорда для плоского угла: 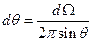, 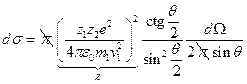; 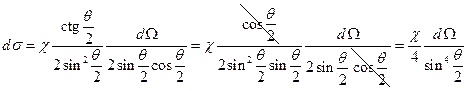, или 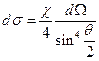(5). Мы получили формулу Резерфорда для телесного угла. Данная формула подтверждается с хорошей точностью и при современных исследованиях. Использовались разные частицы, двигавшиеся с различными скоростями, и формула была в согласии с полученными результатами. Таким образом, косвенно подтвердилось уравнение (4), которое было выведено исходя из соображений планетарного строения атома, что и утвердило главенствующее положение этой теории. Если известно сечение рассеяния 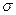, то с помощью формул (4) и (5) можно вычислить зарядовое число 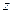. Эксперименты Резерфорда показали, в частности, что элементы в таблице Менделеева изменяются по порядку зарядового числа.