НАПРАВЛЕННЫХ ГРАФОВ

АНАЛИЗ ЭЛЕКТРОННЫХ СХЕМ МЕТОДОМ

В методе направленных графов для адекватного представления анализируемой схемы используется некоторая топологическая структура – граф, состоящий из множества вершин и направленных ветвей. Близость графов и электронных схем обусловлена тем, что любая электронная цепь представляет собой, прежде всего понятие топологическое, т.к. в ней всегда могут быть выделены два пересекающихся множества: узлы и ветви. На этих множествах по некоторому закону организована электронная структура.

Переход от исходной схемы к её графу осуществляется на основе уравнений элементов, входящих в схему, и зависимостей между токами и напряжениями, учитывающих соединения между элементами. Искомые функции схемы можно получить либо последовательным преобразованием графа к эквивалентной ветви, либо применением формулы передачи графа. Используемый для этих целей аппарат направленных графов подменяет математические действия с уравнениями схемы топологическими действиями над элементами графа: его вершинами и ветвями. Схемные функции, так же, как и свойства графов, определяются связями двух указанных множеств.

6.1 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Направленным сигнальным графом (или просто-направленным графом) называют совокупность направленных ветвей (дуг, ребер …), изображаемых отрезками прямых или дугами произвольной кривизны со стрелками, и вершин (узлов), в которых начинаются и кончаются ветви. Таким образом, любой граф содержит два множества: а) множество связанных элементов, т.е. множество вершин, изображаемых точками или кружками, и б) множество связывающих элементов, т.е. множество ветвей.

Для того чтобы определить (задать, описать …) граф, следует задать:

а) множество вершин;

б) множество ветвей;

в) закон (предикат), устанавливающий взаимную принадлежность элементов этих множеств.

Обычно предикат является логическим высказыванием следующего типа: ветвь а_к соединяет вершины x_i и x_j.

Как правило, направленный граф используется для графической записи системы линейных алгебраических уравнений. Вершинами графа бывают представлены независимые и зависимые переменные, входящие в уравнения. Ветви графа отображают коэффициенты уравнений.

Рядом с каждой вершиной и стрелкой ветви проставляются соответствующие буквы или цифры. Буквы или цифры, стоящие рядом со стрелками ветвей, задают коэффициенты передачи ветвей (или просто – передачи ветвей), равные коэффициентам уравнений, отображаемых графом.

Вершина графа, связанная с направленными от нее ветвями, отображает независимую переменную и называется истоком.

Вершина графа, связанная с ветвями, направленными в эту вершину, отображает зависимую (искомую) переменную и носит название стока. Однако вершины, отображающие искомые переменные, т.е. стоки, могут быть связаны с ветвями, которые направлены и от этих вершин. Поэтому, говоря о связи ветвей и вершин, можно говорить о ветвях, исходящих из вершины, и ветвях, заходящих в вершину.

В качестве разновидностей элементов в графе могут быть выделены и другие элементы. Путем в графе называется последовательность элементов (вершин и ветвей), позволяющих совершить через них проход в определенном направлении. Путей в графе может быть несколько. В графе рис.6.1 это могут быть: 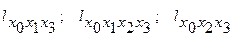и др. Здесь буква l- символ пути, а последовательность нижних индексов, указывает порядок прохождения узлов графа.

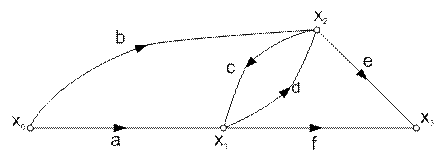
Рисунок 6.1

В качестве количественных характеристик пути часто используются такие понятия, как длина пути и вес (или мера) пути. Число ветвей образующих путь, называют длиной пути. Вес (или мера) пути есть передача пути, равная произведению передач ветвей, входящих в путь.

Путь может содержать несколько ветвей, одну ветвь и в вырожденном виде - одну вершину.

Путь называют разомкнутым, если ни одна из проходящих вершин не встречается более одного раза. Разомкнутый путь может быть прямым и обратным. В последнем случае проходят в обратном порядке.

Путь, начинающийся и заканчивающийся в одной и той же вершине и не проходящий дважды через другие вершины, является замкнутым путем или контуром.

Контур, состоящий из одной ветви, называется петлей. На рис.6.2 показаны примеры пути графа.

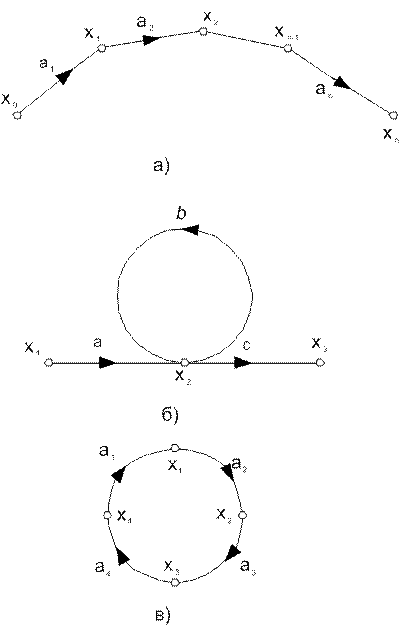
Рисунок 6.2

Каждой вершине графа соответствует величина x_i – сигнал вершины; каждой ветви графа соответствует величина k_ij – передача ветви. Для одиночной ветви можно записать: k_ij= x_j/x_i или x_j = k_ijx_i.

Если в одну вершину (обозначим ее х_j) сходится несколько направленных к ней ветвей, то сигнал этой вершины определится суммой:

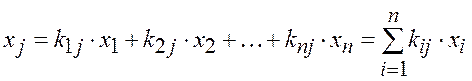.(6.1)

При этом ветви, выходящие из вершины x_j, на величину сигнала этой вершины не влияют, т.е. индекс «i» в равенстве (6.1) соответствует номерам вершин, которые являются начальными вершинами ветвей, оканчивающихся в j-й вершине.

Равенство (6.1) указывает способ записи системы алгебраических уравнений, соответствующих заданному графу, и обратно - способ построения графа для данной системы линейных алгебраических уравнений. Пусть, например, задан граф, приведенный на рис. 6.3 (здесь в обозначении вершин графа опущена буква « х »).

Рисунок 6.3

Записав выражения для сигналов всех вершин графа, получим систему уравнений, соответствующую этому графу:

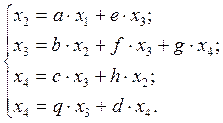
Если система уравнений задана, то соответствующий ей граф можно построить, рассматривая поочередно каждое уравнение и отображая его графически для соответствующей вершины. Таким образом, существует взаимное однозначное соответствие между системой линейных алгебраических уравнений и направленным графом.

В целом граф топологически отображает передачу сигналов от источников к стокам. В связи с этим направленные графы, применяемые для анализа схем, часто называют графами прохождения сигналов.

Как видно из равенства (6.1), уравнения графа составляются для зависимых вершин так, что их сигналы записываются через сигналы других вершин (как зависимых, так и независимых). Пусть записывается уравнение для i-й вершины. Наличие в правой части уравнения для i-й вершины члена k_iix_i означает, что с этой вершиной связана петля, передача которой равна k_ii.

Граф является не геометрической, а топологической фигурой. Существенные свойства графа отображают только направления ветвей и характер связи между вершинами. Важно лишь то, из какой вершины выходит данная ветвь и в какую вершину она входит. Сами ветви могут изображаться отрезками произвольной конфигурации и длины. Графы, в которых направление ветвей и характер связи вершин одни и те же, называются тождественными в топологическом смысле.