Нечеткие отношения, их свойства и операции над ними. Нечеткие графы.
Аппарат теории нечётких отношений используется при построении теории нечётких автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений.
Пусть 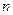 -арное отношение
-арное отношение 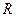 является подмножеством декартова произведения
является подмножеством декартова произведения 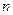 множеств:
множеств: 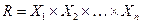 . Подобно нечёткому множеству, нечёткое отношение можно задать с помощью его функции принадлежности, где в общем виде
. Подобно нечёткому множеству, нечёткое отношение можно задать с помощью его функции принадлежности, где в общем виде 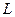 – полная дистрибутивная решетка,
– полная дистрибутивная решетка, 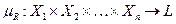 , т. е.
, т. е. 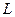 – частично упорядоченное множество, в котором любое непустое подмножество имеет наибольшую нижнюю и наименьшую верхнюю грани, а операции объединения и пересечения в
– частично упорядоченное множество, в котором любое непустое подмножество имеет наибольшую нижнюю и наименьшую верхнюю грани, а операции объединения и пересечения в 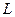 удовлетворяют законам дистрибутивности.
удовлетворяют законам дистрибутивности.
Все операции над нечёткими отношениями определяются с помощью этих операций из 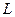 (дистрибутивной решётки).
(дистрибутивной решётки).
Например, если в качестве 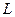 взять ограниченное множество вещественных чисел, то операциями пересечения и объединения в
взять ограниченное множество вещественных чисел, то операциями пересечения и объединения в 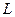 будут соответственно операции минимума (
будут соответственно операции минимума ( 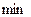 ) и максимума (
) и максимума ( 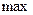 ). Эти операции определяют операции над нечёткими отношениями. В дальнейшем ограничимся рассмотрением лишь бинарных нечётких отношений, являющихся отображением на отрезок
). Эти операции определяют операции над нечёткими отношениями. В дальнейшем ограничимся рассмотрением лишь бинарных нечётких отношений, являющихся отображением на отрезок 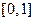 , т. е.
, т. е. 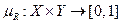 .
.
Если множества 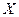 и
и 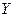 конечные, то нечёткое отношение
конечные, то нечёткое отношение 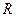 между
между 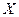 и
и 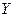 можно представить с помощью его матрицы отношения. Первой строке и первому столбцу ставятся в соответствие элементы множеств
можно представить с помощью его матрицы отношения. Первой строке и первому столбцу ставятся в соответствие элементы множеств 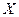 и
и 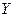 , а на пересечении строки и столбца помечается элемент:
, а на пересечении строки и столбца помечается элемент:
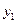
| 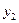
| 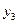
| 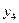
| |
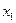
| 0,5 | 0,8 | ||
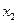
| 0,7 | 0,6 | 0,3 | |
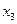
| 0,7 | 0,4 |
В случае, если множества 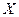 и
и 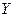 совпадают, нечёткое отношение
совпадают, нечёткое отношение 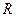 называют нечётким отношением на множестве
называют нечётким отношением на множестве 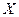 . В случае конечных или счётных универсальных множеств очевидна интерпретация нечёткого отношения в виде взвешенного графа, в котором каждая пара вершин
. В случае конечных или счётных универсальных множеств очевидна интерпретация нечёткого отношения в виде взвешенного графа, в котором каждая пара вершин 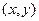 из
из 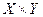 соединяется ребром с весом
соединяется ребром с весом 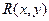 .
.
Пример: пусть 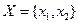 ,
,  , тогда нечёткий граф задает некоторое нечёткое отношение
, тогда нечёткий граф задает некоторое нечёткое отношение 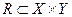 .
.
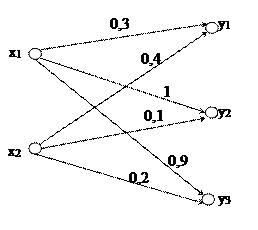
Все элементы 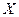 находятся в некотором отношении с элементами
находятся в некотором отношении с элементами 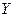 .
.
Операции над нечёткими отношениями:
объединение:
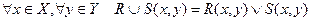 ;
;
пересечение:
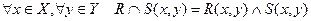 ;
;
отношение включения 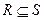 определяется с помощью отношения частичного порядка на
определяется с помощью отношения частичного порядка на 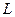 :
:
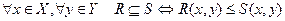 .
.
Множество всех нечётких отношений между 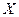 и
и 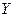 образует дистрибутивную решетку по отношению к операциям объединения и пересечения, и удовлетворяет следующим тождествам:
образует дистрибутивную решетку по отношению к операциям объединения и пересечения, и удовлетворяет следующим тождествам:
1. Идемпотентность:
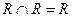 ;
; 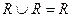 .
.
2. Коммутативность:
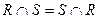 ;
; 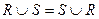 .
.
3. Ассоциативность:
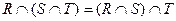 ;
; 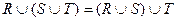 .
.
4. Дистрибутивность:
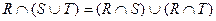 ;
; 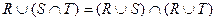 .
.
Свойства нечётких отношений.
Различные типы нечётких отношений определяются с помощью аналитических свойств обычных отношений, причём для нечётких отношений можно указать различные способы обобщения этих свойств.
Нечёткое отношение 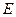 такое, что
такое, что 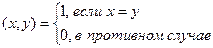 называется отношением равенства.
называется отношением равенства.
1. Рефлексивность:
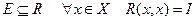 .
.
2. Слабая рефлексивность:
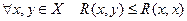 .
.
3. Сильная рефлексивность:
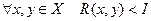 .
.
4. Антирефлексивность:
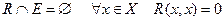 .
.
5. Слабая антирефлексивность:
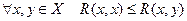 .
.
6. Сильная антирефлексивность:
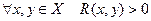 .
.
7. Симметричность:
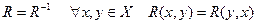 .
.
8. Антисимметричность:
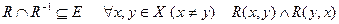 .
.
9. Асимметричность:
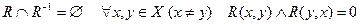 .
.
10. Сильная линейность:
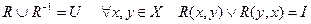 .
.
11. Слабая линейность:
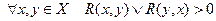 .
.
12. Транзитивность:
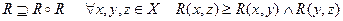 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Операции над нечеткими множествами. | | | Нечеткая логика. Подходы к реализации нечеткого логического вывода. |
Дата добавления: 2015-12-16; просмотров: 2230;
