Нечеткая логика. Подходы к реализации нечеткого логического вывода.

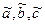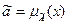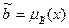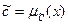Для того, чтобы перейти к нечёткой логике, нужно ввести нечёткие пропозициональные переменные. Нечёткие пропорциональные переменные – это , , . При таком определении переменные 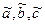начинают принимать не только классические значения 0 и 1, но и любые другие из интервала (0, 1).

Полагаем, что 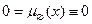и .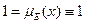

Определяем нечёткие логические операции:

,

,

.

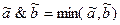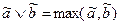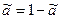Мы можем теперь ввести понятие нечёткой формулы:

1. нечёткая пропорциональная переменная – есть (атомарная) нечёткая формула;

2. есл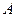и и 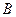– нечёткие формулы, то 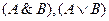и 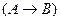– также нечёткие формулы;

3. если 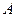– нечёткая формула, то 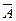– также нечёткая формула.

Справедливы следующие тождества:

свойство коммутативности конъюнкции:

;

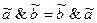свойство коммутативности дизъюнкции:

;

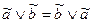свойство ассоциативности конъюнкции:

;

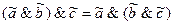свойство ассоциативности дизъюнкции:

;

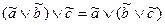законы дистрибутивности:

;

;

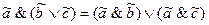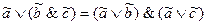законы идемпотентности:

;

;

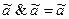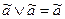закон двойного отрицания:

;

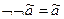законы де Моргана:

;

;

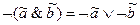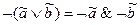свойства констант:

;

;

;

.

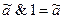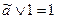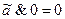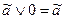Однако

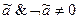(кроме 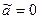или );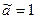

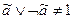(кроме 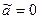или ).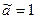

Т. о., нечёткая логика высказываний является классической.

Нечётко релейно-контактные схемы.

Поставим в соответствия формуле 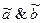– последовательную, а формуле 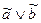– параллельную релейно-контактную схемы:

1. последовательная:

;

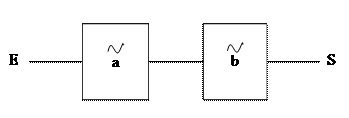
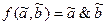2. параллельная:

.

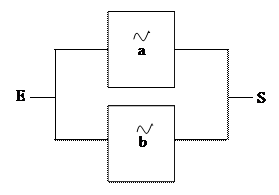
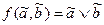В этих схемах указывается вход 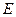и выход 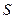. Результат выполнения нечётких логических операций называется током схемы.

Если взять 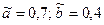, то для последовательной схемы ток 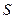равен 0,4, а для параллельной – 0,7. В случае классической логики ток мог принимать только значения 0 и 1.