Эйлеровы и гамильтоновы цепи и циклы.

Теорема Эйлера

Рассмотрим задачу о кенигсбергских мостах, сформулированную Эйлером. Река Прегель делит г. Кенигсберг на четыре части: A, B, C, D, соединенные между собой семью мостами (рис. 3.1.5).

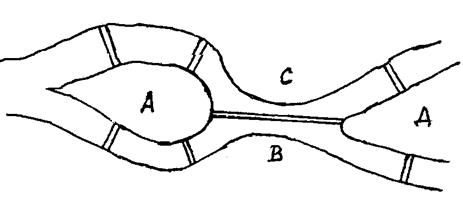
Рис. 5

Требуется определить, можно ли, выйдя из какой-либо части города, пройти по всем мостам по одному разу и вернуться в исходную часть города. Решая эту задачу, Эйлер доказал теоремы, позволяющие установить, для каких графов существуют эйлеровы циклы и цепи.

Теорема 1. Чтобы неориентированный граф обладал эйлеровым циклом, необходимо и достаточно, чтобы он был связан, и все вершины графа имели четные степени.

Для существования эйлерова контура на ориентированном графе необходимым и достаточным условием являются связность графа и равенство полустепеней захода и исхода в каждой вершине. Очевидно, что степени вершин графа четны.

Граф, соответствующей задаче Эйлера о кенигсбергских мостах, не удовлетворяет теореме 1. Он не содержит эйлерова цикла.

Теорема 2. Неориентированный граф содержит эйлерову цепь, соединяющую вершины А и В в том и только в том случае, если граф связен, и только эти вершины А и В являются вершинами с нечетными степенями, а степени всех остальных вершин четны.

Алгоритм построения эйлерова цикла состоит в следующем:

1. Выходим из произвольной вершины X₀, каждое пройденное ребро зачерчиваем.

2. Никогда не идем по такому ребру, которое в рассматриваемый момент является перешейком, а также не выбираем ребра, идущего в X₀, пока есть другие возможности.

Задача об определении гамильтоновых линий в общем виде не решена. Для каждого графа она решается отдельно. Получены некоторые необходимые, некоторые достаточные условия существования гамильтоновых графов, т.е. графов, содержащих гамильтонов цикл. К полученным результатам относится теорема Кенига: в полном графе (т.е. в графе, любая пара вершин которого соединена хотя бы в одном направлении) всегда существует гамильтонов путь.

К числу задач, требующих определения гамильтонова цикла, относится задача о коммивояжере. Бродячий торговец, предлагая товар, посещает ряд городов, причем каждый город он посещает единственный раз, после чего вновь возвращается в исходный пункт. Требуется определить кратчайший путь коммивояжера, если расстояния между городами заданы. Города можно представить как вершины связного неориентированного графа, в котором каждый паре вершин x_ix_j приписывается расстояние l(x_i,x_j). Эта задача имеет ряд важных приложений в экономике, к ней, в частности, сводится задача о наиболее эффектном использовании подвижного состава оборудования. Решается задача методами динамического программирования.

Изоморфизм графов.

Два графа называются изоморфными, если между их вершинами можно установить взаимно однозначное соответствие, сохраняющее смежность, т.е. два графа G(x,u) и G'(x',u') изоморфны, если существует такое взаимно однозначное соответствие j

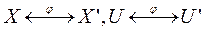, что если 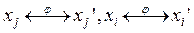, то

,

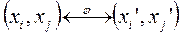где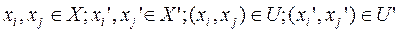

Изоморфные графы несут одну и ту же информацию, поэтому они могут рассматриваться как один граф. Графы различаются с точностью до изоморфизма.

Планарность. Плоские графы.

Говорят, что граф укладывается на поверхности S, если его можно нарисовать на S так, что никакие два его ребра не пересекаются в точках, не являющихся вершинами графа.

Граф называется планарным, если его можно уложить на плоскости. Плоский граф – граф, уложенный на плоскости.

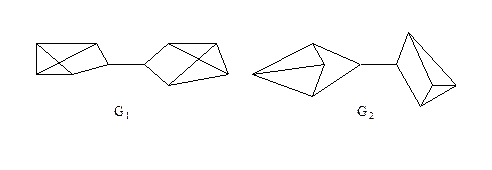
Рис. .6.

Граф G1 (рис. 3.1.6) планарен, он изоморфен плоскому графу G2. Исследование планарности графов составляет одну из задач этой теории. Изучение планарных графов было начато Эйлером. Опираясь на результаты, полученные Эйлером, можно доказать, что графы K1, K2, K3 (рис. 3.1.7) не являются планарными. Заметим, что графы K1, K3 изоморфны.

Рис.7.

Графы, изоморфные указанным графам, также не являются планарными.

Отыскание общего критерия планарности графов составляло одну из труднейших задач теории графов. Решение было найдено Понтрягиным и независимо от него Куратовским. Чтобы сформулировать эти результаты, необходимо познакомиться с определением гомеоморфизма. Но прежде сформулируем следующие определения.

Говорят, что граф G'(x',u') получен из графа G(x,u) операцией подразделения ребра (x_i,x_j)Îu, если x'=xÈa, u'=u[(x_i,x_j)È(x,.a)È( a,x_j)]

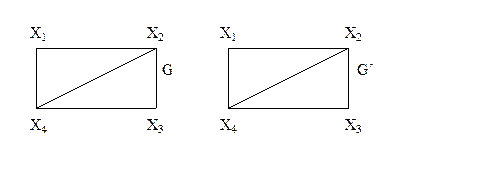
Рис. .8.

Два графа G1,G2 называются гомеоморфными, если существует такой граф G', который может быть получен как из графа G1, так и из G2 операцией подразделения ребра конечное число раз. Или: графы G1 и G2 гомеоморфны, если существуют изоморфные подразбиения G1' и G2', изображенные на рис. 3.1.9, гомеоморфны.

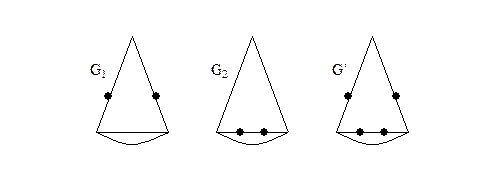
Рис. 9

Граф G' может быть получен из графов G1 и G2 операцией подразделения ребра, проведенной дважды.

Теорема Понтрягина-Куратовского. Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного графам K1 или K2 (рис.3.1.7).

Вслед за этим классическим результатом были предложены другие критерии планарности.