Операции над графами. Объединение графов.

Объединением графов G1(x₁,г₁x₁) и G2(x₂,г₂x₂) называется такой граф G(x,гx), у которого множество вершин есть сумма множеств вершин объединяемых графов x=x₁Èx₂, а отображение есть сумма отображений объединяемых графов гx=г₁x₁Èг₂x₂. обозначает: G=G1ÈG2.

Пример. Заданы графы G1 и G2:

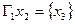
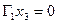
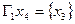
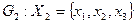
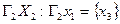
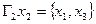
Требуется определить G(x,гx)=G1ÈG2.

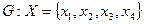
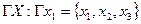
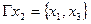
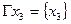
Геометрическая реализация складываемых графов и графа-суммы имеет следующий вид:

Рис. 14

Граф-сумма содержит все вершины и дуги, встречающиеся хотя бы в одном из двух складываемых графов.

Пересечение (произведение) графов.

Пересечением графов G1(x₁,г₁x₁) и G2(x₂,г₂x₂) называется такой граф G(x,гx), у которого множество вершин есть пересечение множеств вершин графов X=X₁ÇX₂, а отображение есть пересечение отображений перемножаемых графов ГX=Г₁X₁ÇГ₂X₂.

Пример.

Пересечение графов G1 и G2 предыдущего примера есть граф G(x,гx):

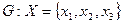
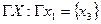
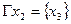
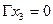
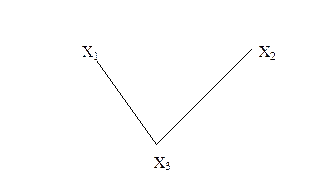Рис. 15.

Граф-пересечение содержит вершины и дуги, являющиеся общими у перемножаемых графов.