Матрицы достижимостей и контрадостижимостей.

Пусть задан граф G(x,г(x)). Говорят, что вершина x_jÎX достижима из вершины x_iÎX, если существует по крайней мере один путь из x_i в x_j. Пусть R(x_i) – множество вершин, достижимых из вершин x_i графа G. Так как каждая вершина графа достижима из себя самой с помощью пути длины нуль, то первым элементом достижимого множества R(x_i) является вершина x_i. Множество вершин x_j, достижимых из x_i с использованием путей длины единица, есть множество Г(x_i). Множество Г(Г(x_i))=Г²(x_i) состоит из вершин, достижимых из x_i с использованием путей длины два и, аналогично, Г^p(x) является множеством вершин, которые достижимы из x_i с помощью путей длины p. Так как вершина графа G, достижимая из вершины x_i должна быть достижима с использованием путей длины нуль, или единица, или два,…, или p, то множество R(x_i) вершин, достижимых из x_i, можно представить в следующем виде:

R(x_i)={x_i}Èг(x_i)Èг²(x_i)È…Èг^p(x_i). (3.1.1)

Для того чтобы получить достижимое множество R(x_i), необходимо в выражении (5.1) последовательно выполнять слева направо операции объединения до тех пор, пока мощность “текущего” множества не перестанет увеличиваться при очередной операции объединения. Это означает, что последующие операции объединения не будут давать новых элементов “текущему” множеству, которое и определяет множество R(x_i). Матрицей достижимостей R= (r_ij) называется квадратная матрица порядка n (n – число вершин графа), элементы которой определяются следующим образом:

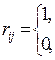
	если ,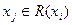
в противном случае

Пример.

Для графа G (рис.3.1.21) построить матрицу достижимостей

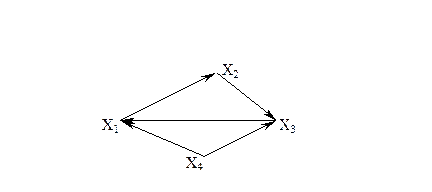
Рис. 21.

Решение.

На основании выражения (3.1.1) находим множества достижимостей :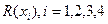

,

,

,

.

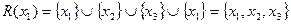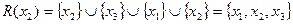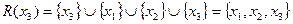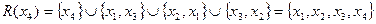Следовательно, матрица достижимостей имеет вид

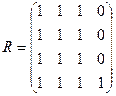
Матрицей контрадостижимостей (обратных достижимостей) Q=(q_ij) называется квадратная матрица порядка n, элементы которой определяются следующим образом:

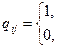
	если ,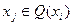
в противном случае

где Q(x_i) – множество таких вершин, что из любой вершины этого множества можно достигнуть вершину x_i.

Контрадостижимое множество Q(x_i) строится на основании следующего выражения:

Q(x_i)={x_i}Èг^-1(x_i)Èг^-2(x_i)È…Èг^-p(x_i). (2)

где г^-1(x_i) – множество вершин, из которых достижима вершина x_i с использованием пути длины единица; г^-2(x_i)=г^-1(г^-1(x_i)) – множество вершин, из которых достижима вершина x_i с использованием пути длины два и т.д.

Пример.

Для графа G (рис..21) построить матрицу контрадостижимостей.

Решение.

На основании выражения (2) находим множества контрадостижимостей Q(x_i),i=1,2,3,4:

,

,

,

.

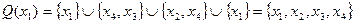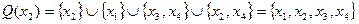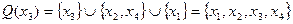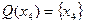Следовательно, матрица контрадостижимостей имеет вид:

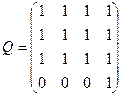
Из определения матриц R и Q следует, что i-й столбец матрицы R совпадает с i-й строкой матрицы Q. Поэтому Q=R^T, где T – знак транспонирования.

Так как R(x_i) является множеством вершин, достижимых из x_i, а Q(x_j) – множеством вершин, из которых достижима вершина x_j, то R(x_i)ÇQ(x_j) является множеством таких вершин, каждая из которых принадлежит по крайней мере одному пути, идущему от x_i к x_j. Эти вершины называются существенными (неотъемлемыми) относительно двух концевых вершин x_i и x_j. Эти вершины называются существенными (неотъемлемыми) относительно двух концевых вершин x_i и x_j. Все остальные вершины x_kÏR(x_i)ÇQ(x_j) называются несущественными (избыточными), так как их удаление не влияет на пути от x_i к x_j.

Деревья