Сети. Отношение порядка между вершинами ориентированного графа.
Ориентированный граф без циклов, имеющий одну вершину без входящих дуг (вход графа) и одну вершину без выходящих дуг (выход графа), называется сетью.
Отыскание экстремальных путей на графах такого вида используется в различных экономических расчетах. К их числу относятся рассмотренная выше задача, а также задачи сетевого планирования.
В любом ориентированном графе для циклов можно установить отношение порядка между его вершинами.
Вершина xi предшествует вершине xj, если существует дуги из xi в xj. Это отношение порядка удовлетворяет аксиомам порядка:
1) если xi предшествует xj, то xj не предшествует xi;
2) если xi предшествует xj, xj предшествует xk, то xi предшествует xk.
“Правильная” нумерация вершин графа заключается в том, что при xi предшествующему xj номера i и j должны удовлетворять неравенству i<j.
На графе-сети практически это можно сделать, используя распределение вершин по рангам методом вычерчивания дуг. Вычеркиваем дуги, исходящие из входа графа, вершины x0. Вершины, соответствующие концам этих дуг и не имеющие после этой операции входящих дуг, относим к вершинам I-го ранга. На графе G (рис.3.3.1) вершинами I-го ранга являются вершины x1 и x2. Вершины I-го ранга получают первые порядковые номера 1,2. Внутри одного ранга нумерация произвольна.
Затем вычеркиваем дуги, выходящие из вершин I-го ранга. Вершины, соответствующие концам таких дуг и не имеющие после этих операций входящих дуг, относим к вершинам 2-го ранга. Они получают следующие порядковые номера. В нашем примере к вершинам 2-го ранга относится одна вершина x3.
Процесс вычеркивания дуг продолжается до тех пор, пока все вершины графа не будут занумерованы. Последний порядковый номер получит вершина xn – выход графа.
В рассмотренном примере все вершины распределены по 4 рангам. К вершинам 3-го ранга принадлежит x4, а к вершинам 4-го ранга – x5.
Существуют и другие способы “правильной” нумерации вершин графа, в том числе алгоритм Форда для нумерации вершин графа.
Задача о пути максимальной длины между двумя вершинами ориентированного графа в сетевом планировании.
Постановка задачи.
Задача ставится следующим образом.
Задан конечный ориентированный граф без контура G(x,u).
Каждой дуге графа “u” ставится в соответствие длина дуги l(u).
Требуется определить длиннейший путь, соединяющий две вершины графа x0 и xn.
Аналогичные задачи можно ставить для ориентированных графов с контурами, а также неориентированных графов. Но в этом случае во избежание бессодержательности задачи нужно вводить дополнительные условия, исключающие пути бесконечной длины.
Решение задачи состоит как в отыскании пути максимальной длинны между двумя фиксированными вершинами графа, так и в определении величины этого пути.
Одну из основных задач сетевого планирования составляет отыскание путей максимальной длины между входом и выходом графа-сети.
Алгоритм.
Каждая вершина графа получает числовую метку, которая может меняться конечное число раз. Установившаяся метка – величина длиннейшего пути из вершины x0 в данную вершину xj. В частности, установившаяся метка вершины xn есть величина длиннейшего пути из x0 в xn.
Чтобы определить искомый путь, нужно рассмотреть последовательность шагов, на каждом из которых ищется одна из дуг длиннейшего пути между x0 и xn.
Алгоритм состоит в последовательном проведении следующих этапов:
1. Полагаем λ0 = 0; λi = -∞ (i = 1,…,n).
2. Ищем дугу (xi, xj) такую, что 
. Если такой дуги нет, то не существует пути, соединяющего x0 и xn. Если такая дуга найдется, то изменяем метку lj на l’j=lj +l(x0,xj).
3. Продолжаем процедуру пункта 2 до тех пор, пока метки вершин xi не перестанут меняться.
Установленные метки обозначим l*i. При этом могут встретиться два случая:
1) l*n= -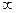 
, это соответствует тому, что пути, соединяющего вершины x0 и xn, не существует;
2) l*n- конечное число. Оно равно длине пути максимальной длины из x0 в xn.
Сам путь находим, отмечая вершины, по которым достигается максимум, т.е. те вершины, для которых
.
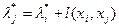Если между вершинами графа-сети установлено отношение порядка, т.е. они “правильно” занумерованы, то решение задачи можно получить за один шаг, произведя подсчет меток с учетом следующей формулы:
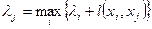(2)
Пример.
Определим длиннейший путь на графе, изображенном на рис.1, а также его длину.
Вначале полагаем для вершины x0 l0=0 и lj=- 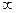для вершин xi (I=1,…,5).
Затем, т.к. l1-l0=- 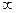<l(x0,x1), меняем метку вершины x1, т.е. l1, на
| l’1=l0+l(x0,x1)=2 | (x0) |
Аналогично l’2=l0+l(x0,x2)=4.
Чтобы найти метку вершины x3, пользуясь формулой (3.3.2)
| l’3=max{[l’1+l(x1,x3)].[ l0+l(x0,x3)]}=max{(2+4),(0+5)}=6 | (x1) |
Справа в скобочках отмечаем вершины, по которым достигается максимум длины.
Аналогично
| l’4=max{[l’1+l(x1,x4)],[ l’3+l(x3,x4)]}=max{(2+3),(6+6)}=12 | (x3) |
| l’5=max{[l’3+l(x3,x5)],[l’4+l(x4,x5)],[l’2+l(x2,x5)]= =max{(6+4),(12+2),(4+7)}=14 | (x4) |
Искомый путь имеет длину l(m)=l*5=14. Причем в x5 он идет из вершины x4, в x4 из x3, в x3 из x1, в x1 из x0: x5,x4,x3,x1,x0. Следовательно m=(x0,x1,x3,x4,x5).
Путь максимальной длины называют критическим путем. Следовательно, критический путь в рассмотренном примере есть m=(x0,x1,x3,x4,x5), а его длина l(m)=14.
Сетевое планирование. Скорейшее время завершения проекта.
Рассмотрим некоторый проект – совокупность операций (работ), составляющий некоторый многошаговый процесс. Примером может служить строительство некоторого объекта. Считаем известными все работы, которые предстоит совершить, их последовательность и время, необходимое для выполнения каждой работы. Проект может быть изображен в виде графа-сети. Зададимся целью определить кратчайший срок завершения проекта.
Пусть данные о строительстве приведены в следующей таблице
| Виды работ | Какие работы следуют за перечисленными | Продолжительность работ |
| 2,3 | ||
| 6,7 | ||
| 6,7 | ||
| - | ||
| - | ||
| - |
Эту информацию о проекте представим в виде графа-сети. Дугами графа будем изображать работы, а вершины графа – некоторые события. Назовем элементарными событиями начало и конец каждой работы, а некоторую совокупность элементарных событий – событием.
Вход графа – событие, заключающееся в начале всего проекта. Оно является событием, стоящим в начале одной или нескольких работ, а именно тех, которые не следуют ни за какими другими, т.е. работ, с которых может быть начато строительство. В нашем примере такими работами являются №1,4,5 (их нет во 2- столбце).
Выходом графа будет являться событие, заключающееся в окончании работ, за которыми не следуют никакие другие работы, т.е. в окончании всего проекта. В данном примере – это работы №7,8,9.
Все другие вершины графа есть события, заключающиеся в окончании одних и начале других работ.
Сетевой граф, соответствующий приведенным в таблице данным, изображен на рис.3.3.2. Номер работы обозначен числом вне кружка. Число, обведенное кружком, есть продолжительность данной работы. Вход графа, вершина x0 – начало проекта. Выход графа, вершина x5 – окончание проекта.
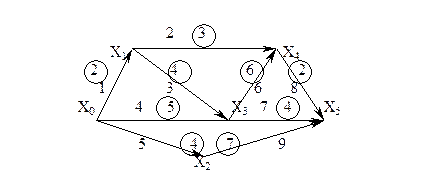
Рис. 2
Вершины x1,x2,x3,x4 есть события, заканчивающиеся в начале одних и окончании других работ. Так, например, вершина x3 есть окончание 3-й и 4-й работ и начало 6-й и 7-й.
Путь максимальной длины из вершины x0 в xi есть скорейшее время наступления события xi. В самом деле, событие x3, например, соответствующее началу 6-й и 7-й работ, может произойти только после окончания 3-й и 4-й работ, а следовательно, и после окончания 1-й, т.к. для выполнения 3-й работы необходимо окончание 1-й работы. Следовательно, скорейшее время наступления события x3 есть
max{5,(2+4)}=6
Скорейшее время наступления события 5 есть скорейшее время окончания проекта в целом и равно длине пути максимальной длины из вершины x0 в x5.
Итак, если x0 и xn есть вход и выход графа-сети, соответствующего данному проекту, то для определения наиболее раннего срока окончания всех работ нужно найти путь максимальной длины из x0 в xn, т.е. критический путь, и определить его длину. Время, соответствующее скорейшему окончанию работ, т.е. скорейшему завершению проекта, называется критическим временем данного проекта. Оно численно совпадает с длиной критического пути из x0 в xn.
В приведенном примере критический путь, проходящий через вершины x0,x1,x3,x4,x5, имеет длину, равную 14 l(m)=14, т.е. критическое время данного проекта равно 14.
Работы, составляющие критический путь, называются критическими работами (операциями). От своевременного выполнения критических операций зависит срок завершения проекта. Они не допускают запаздывания в исполнении в отличие от некритичных операций.
С другими параметрами сетевого графа, правилами составления графа-сети, а также вопросами сетевого планирования в целом читатель может ознакомиться по списку литературы.
Дата добавления: 2016-01-26; просмотров: 1799;