Основные определения и теоремы.
Неориентированный граф с числом вершин n>1 называется деревом, если он связен и не содержит циклов.
Следующая теорема характеризует свойства деревьев, каждое из которых может служить определением дерева.
Теорема 1.Для графа G, имеющего n вершин (n>1), равносильны следующие свойства:
1. G связен и не содержит циклов;
2. G не содержит циклов и имеет (n-1) ребро;
3. G связен и имеет (n-1) ребро
4. G не содержит циклов, но добавление ребра между любыми его вершинами приводит к образованию цикла;
5. G связен, и все его ребра являются перешейками;
6. Всякая пара вершин G соединена только одной цепью.
Доказательство этой теоремы можно провести, показав цепочку следствий 1→2→3→4→5→6→1.
Доказательство. Если граф G связен и не имеет циклов, то цикломатическое число ν=N-n+1=0, откуда N=n-1, т.е. G не содержит циклов и имеет (n-1) ребро (1→2).
Если G не имеет циклов, то ν=0, причем N=n-1, т.е. ν=N-n+P=0, откуда получаем P=1, т.е. G связен и имеет (n-1) ребро (2→3).
Если G связен и имеет (n-1) ребро, то ν=N-n+1, N=n-1. Отсюда ν=0, т.е. G не содержит циклов. Если добавить одно ребро, получим связной граф G’ с числом ребер N’=n. Цикломатическое число этого графа ν’=n-n+1=1, т.е. G’ содержит один цикл(3→4).
Если G не содержит циклов, но добавление одного ребра ведет к образованию цикла, то G связен так как в противном случае в графе G должны существовать две вершины Xi и Xj , не соединенные никакой цепью и такие, что добавление ребра(Xi Xj) не привело бы к образованию цикла. Все ребра графа являются перешейками, т.к. удаление любого из них приводит к графу G’, для которого ν’=N-n+P=0, причем N’=N-1. так как G связен и не содержит циклов, ν’=N-n+1=0, откуда N=n-1, N’=n-2 и, следовательно, P=2.т.е. G’ не является связным (4→5).
Если G связен, то всякая пара его вершин соединена цепью. В силу того, что все ребра G являются перешейками, существует единственная цепь, соединяющая любую пару вершин Xi, Xj , т.к. в противном случае удаление ребра (Xi Xj) не нарушило бы связности графа G (5→6).
Если всякая пара вершин G соединена цепью, то G связен. Так как такая цепь единственная, G не содержит циклов: если бы G содержал циклы, то в нем нашлась бы пара вершин Xi, Xj , соединенная более чем одной цепью (6→1), что и требовалось доказать.
Ориентированное дерево называется прадеревом.
Несвязный граф, компонентами связности которого являются деревья, называется лесом.
В дальнейшем понадобится следующее определение: подграф G’(X’,U’) содержащий все вершины графа G(X,U), называется частичным графом.
Теорема 2. Граф G(X,U) тогда и только тогда содержит частичный граф, являющийся деревом, когда он связен.
Доказательство. Если граф G содержит частичный подграф-дерево, то, очевидно, он связен, т.к. на основе свойства 6 предыдущей теоремы каждая пара его вершин может быть соединена цепью.
Предположим теперь, что граф связен. Докажем, что он содержит частичный граф-дерево.
Если граф G не содержит циклов, то он сам является деревом по определению. Предположим, что G содержит цикл μ. Вычеркнем из μ любое ребро. Получившийся частичный граф G1 ,будет связным, т.к. удаление из цикла любого ребра не нарушает связности графа. Если G1 – дерево, доказательство закончено. Если G1 содержит циклы, то удаляем ребро любого из них и получаем подграф G2 . Если G2 не имеет циклов, то он есть дерево и доказательство закончено. Если G2 содержит циклы, то удаляем ребро одного из них, и.т.д.
Через несколько шагов получим связной граф без циклов, т.е. дерево, являющееся подграфом исходного графа G.
Постановка задачи.
Предположим, что имеется n городов, которые нужно соединить нефтепроводом (электролинией, газопроводом). Стоимость строительства нефтепровода между городами Xi, Xj задана. Как построить самый дешевый нефтепровод, связывающий все города?
Построим граф, вершинами которого обозначены города, а ребрами возможные нефтепроводы между ними. Каждому ребру графа (Xi, Xj) поставим в соответствие число l(Xi, Xj)≥0, равное стоимости строительства нефтепровода на участке (Xi, Xj). Задача строительства самого дешевого нефтепровода сводится к следующей задаче на графе. Задан конечный неориентированный связной граф G(X,U) каждому ребру которого (Xi,Xj)=U поставлено в соответствие число l(U)≥0, называемое длинной ребра. Требуется найти такой частичный граф-дерево графа G (частичное дерево), общая длина ребер которого минимальна. Решение этой задачи может быть получено с помощью следующего алгоритма.
Алгоритм Краскала
Алгоритм построения кратчайшего дерева для графа G(X,U) состоит в следующем:
1. Выбираем самое короткое ребро графа U1 , затем ребро U2, затем самое короткое из оставшихся;
2. Из оставшихся ребер выбираем самое короткое ребро U3 так, чтобы оно не образовывало цикла с выбранными ребрами;
3. Продолжаем эту процедуру. На k-м к выбранным ребрам U1,…,Uк-1 добавляем самое короткое ребро из оставшихся │U│-(к-1) ребер так, чтобы оно не образовывало цикла с выбранными ребрами;
4. При k=n-1 процесс заканчивается. Получим граф без циклов с (n-1)-м ребром. На основании теоремы 1 (пункт 2) построенный граф есть дерево, обозначим его T(n-1).
Докажем, что построенное по этому графу дерево T(n-1) кратчайшее.
1.Сначала предположим что G – полный граф, и длины всех его ребер различны. Для доказательства воспользуемся методом от противного. Предположим, что построенное T(n-1) дерево не кратчайшее и имеется отличное от него кратчайшее дерево T. В этом существует две возможности:
а) T и Т(n-1) не имеют общих ребер. Присоединим к дереву Т ребро U1Є Т(n-1). В этом случае согласно пункту 4 теоремы 1 в получившемся графе имеется цикл, одним из ребер которого является U1. Выбросим из этого цикла любое ребро U’≠U1.В результате этой операции получим частичное дерево Т', которое отличается от Т одним ребром: u’ заманено U1. Но l(U1)<l(U') , т.к. U1 – кратчайшее ребро. Следовательно, l(T')<l(T) т.е. Т не кратчайшее дерево;
б) Т и Т(n-1) имеют общие ребра U1 , U2 ,…, U(k-1). Пусть Uк есть первое ребро, принадлежащее Т(n-1), но не принадлежащее Т.
Рассмотрим граф, который получится присоединением к дереву Т ребра Uк, т.е.  . В соответствии с пунктом 4 теоремы 1 в нем есть цикл μ, причем μ содержит ребро U’, не принадлежащее Т(n-1), т.к. в противном случае дерево Т(n-1) содержало бы цикл, что противоречит определению дерева.
. В соответствии с пунктом 4 теоремы 1 в нем есть цикл μ, причем μ содержит ребро U’, не принадлежащее Т(n-1), т.к. в противном случае дерево Т(n-1) содержало бы цикл, что противоречит определению дерева.
Удалив из цикла μ ребро U’, получим дерево 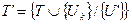 , отличающееся от Т одним ребром: U' заменено на Uk. Но l(Uk)<l(U’) , т.к. в противном случае на k-м шаге при построении дерева Т(n-1) в него включили бы ребро U’. Следовательно, l(Т')<l(Т), т.е. Т – не кратчайшее дерево.
, отличающееся от Т одним ребром: U' заменено на Uk. Но l(Uk)<l(U’) , т.к. в противном случае на k-м шаге при построении дерева Т(n-1) в него включили бы ребро U’. Следовательно, l(Т')<l(Т), т.е. Т – не кратчайшее дерево.
2. Пусть G(X,U)- неполный граф, но его ребра имеют разную длину. Пусть l(U)=L –сумма длин всех ребер графа G. Присоединим к G столько новых ребер, сколько требуется для получения полного графа. Припишем каждому вновь построенному ребру длину lj>L.
В полученном полном графе построим кратчайшее дерево Т(n-1).
На основании теоремы 2 в графе G есть кратчайшее дерево, длина которого не превосходит L. Частичное дерево графа G будет являться частичным деревом для построенного полного графа. Поэтому ни одно новое ребро в кратчайшее дерево входить не может. Следовательно, для построения кратчайшего частичного дерева в графе G можно пользоваться алгоритмом Краскала.
3. Предположим теперь, что некоторые ребра графа G(X,U) имеют одинаковую длину. Пусть Δ – минимальная ненулевая разность длин ребер. Обозначим 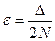 , где N=│U│. Пусть l1,…,lm – все значения длин ребер графа; kj принимают значение lj. Занумеруем ребра графа в порядке увеличения длины. Затем изменим длину ребра графа следующим образом:
, где N=│U│. Пусть l1,…,lm – все значения длин ребер графа; kj принимают значение lj. Занумеруем ребра графа в порядке увеличения длины. Затем изменим длину ребра графа следующим образом:  . В получившемся графе длины всех ребер различны. Выберем с помощью алгоритмов Краскала кратчайшее частичное дерево. Проведенное изменение длин ребер графа обладает тем свойством, что если в исходном графе
. В получившемся графе длины всех ребер различны. Выберем с помощью алгоритмов Краскала кратчайшее частичное дерево. Проведенное изменение длин ребер графа обладает тем свойством, что если в исходном графе  , то и в графе с ребрами измененной длины
, то и в графе с ребрами измененной длины 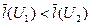 . Следовательно, кратчайшее частичное дерево в новом графе будет кратчайшим и в старом.
. Следовательно, кратчайшее частичное дерево в новом графе будет кратчайшим и в старом.
В графе, где некоторые ребра имеют одинаковую длину, кратчайшее частичное дерево может не быть однозначно определенным.
Пример
Требуется построить газопровод, соединяющий 10 городов (рис.1.). Возможные соединения городов обозначены ребрами, длины которых l(Xi,Xj), представляющие собой стоимость строительства газопровода на участке (Xi,Xj), заданы и обозначены на графе. Как построить самый дешевый газопровод?
Задача сводится к отысканию частичного дерева заданного графа, общая длина ребер которого минимальна. Воспользуемся алгоритмом Краскала.
Частичное дерево должно содержать (n-1) ребер, т.е. 9. общее число ребер исходного графа 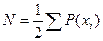 .
.
 Рис. .1
Рис. .1
Заданные длины ребер удобно поместить в следующую симметрическую таблицу, в которой достаточно заполнить один из углов – верхний или нижний по отношению к главной диагонали (рис.3.2.2). На пересечении строки Xi и столбца Xj стоит число, равное длине дуги (Xi,Xj), т.е. l(Xi,Xj). Число заполненных клеток равно числу ребер графа. Следуя алгоритму, выбираем самые короткие ребра U1=(X1,X2), U2=(X4,X6), l(U1)=l(U2)=1.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | ||||
| X1 | |||||||||||||
| X2 |
| ||||||||||||
| X3 |
| ||||||||||||
| X4 | |||||||||||||
| X5 |
|
| |||||||||||
| X6 |
| ||||||||||||
| X7 |
| ||||||||||||
| X8 | |||||||||||||
| X9 | |||||||||||||
| X10 |
|
|
|
Рис. 2.
Отметим это, зачеркнув выбранные числа в таблице и пометив выбранные ребра на графе жирной чертой. Наименьшее из оставшихся чисел в таблице есть 2, т.е. длина дуги (X1,X3). Выбираем в качестве U3 ребро (X1,X3), т.к. оно не образует цикла с выбранными ребрами. Вновь делаем отметку в таблице и на графе и т.д. Получим в результате U4=(X9,X10), U5=(X1,X10), U6=(X4,X5), U8=(X8,X10), U7=(X2,X5), U9=(X7,X6).
Длина последнего выбранного ребра равна 9, т.к. ребра графа с меньшими длинами 6,7,8 не могут являться ребрами дерева. Сумма длин ребер построенного дерева L=34. Стоимость строительства самого дешевого газопровода по исходным данным составляет 34 денежные единицы.
Дата добавления: 2016-01-26; просмотров: 1138;
