Удаление узлов из BST

Для реализации удаления первым шагом является поиск узла. Однако, при удалении узла мы также обязаны сохранить выполнение характеристического свойства, какова бы ни была структура дерева и местоположение удаляемого узла.

Случаи, когда удаляется листовой узел, тривиальны. Удаляемый узел просто отцепляется от родителя. Например, удаление узла 8 не вызывает никаких сложностей:

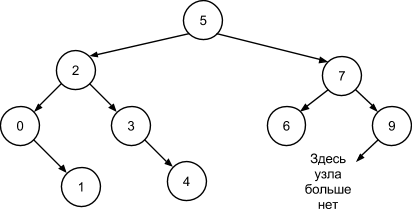
Если удаляется узел-родитель, имеющий только одно из поддеревьев, то корень поддерева становится на место узла-родителя. Удалим узел с ключом 3:

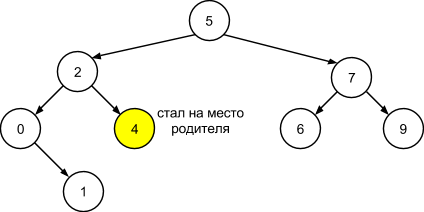
Если же удаляется узел-родитель, имеющий оба поддерева, следует на его место поставить узел с минимальным ключом из правого поддерева. Фактически, необходимо найти узел, являющийся следующим относительно удаляемого при симметричном обходе. Допустим удаляется корневой узел 5, на его место становится узел 6, являющийся минимальным в правом поддереве 9. Особую аккуратность при переназначении связей в деревьях следует проявить, если следующим узлом является непосредственный правый дочерний узел удаляемого узла.

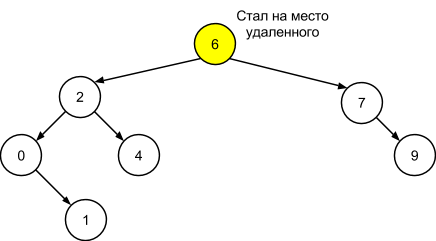
Следует отметить, что алгоритм принципиально не изменится, если вместо следующего узла (минимального узла из правого поддерева) будет использоваться предыдущий (максимальный узел из левого поддерева), поскольку такая замена является симметричной.

Ниже приведена реализация описанного алгоритма удаления узла:

// Вспомогательная функция пересадки узла:

// заменяет все ссылки на указанный узел на ссылки на другой узел (либо на nullptr)

voidBSTreeTransplant ( BSTree & _tree,
BSTree::Node * _pNode,
BSTree::Node * _pOtherNode )

{

// Если у пересаживаемого узла нет родителя, значит он является корневым

if( ! _pNode->m_pParent )

{

// Подменяем корневой узел

assert( _pNode == _tree.m_pRoot );

_tree.m_pRoot = _pOtherNode;

}

// Пересаживаемый узел является левым дочерним у своего родителя?

else if( _pNode->m_pParent->m_pLeft == _pNode )

// Левым дочерним узлом родителя будет другой узел

_pNode->m_pParent->m_pLeft = _pOtherNode;

// Пересаживаемый узел является правым дочерним у своего родителя?

else if( _pNode->m_pParent->m_pRight == _pNode )

// Правым дочерним узлом родителя будет другой узел

_pNode->m_pParent->m_pRight = _pOtherNode;

// Других случаев быть не может!

Else

assert( 0 );

// Новым родителем пересаженного узла является родитель прежнего узла

if( _pOtherNode )

_pOtherNode->m_pParent = _pNode->m_pParent;

}

// Удаление указанного ключа из дерева

voidBSTreeDeleteKey ( BSTree & _tree, int_key )

{

// Обнаруживаем узел с интересующим ключом

BSTree::Node * pNode = BSTreeFindKeyNode( _tree, _key );

if( ! pNode )

// Узел не найден, игнорируем запрос (либо сообщаем об ошибке)

return;

// Если у удаляемого узла нет левого поддерева, подменяем его правым поддеревом.

// Даже если правого поддерева нет, пересадка корректно переназначит связи.

if( ! pNode->m_pLeft )

BSTreeTransplant( _tree, pNode, pNode->m_pRight );

// Если у удаляемого узла нет правого поддерева, подменяем его левым поддеревом.

else if( ! pNode->m_pRight )

BSTreeTransplant( _tree, pNode, pNode->m_pLeft );

// Самый сложный случай - удаляемый узел имеет и левое, и правое поддерево

Else

{

// Ищем минимальный узел в правом поддереве удаляемого узла

BSTree::Node * pNextNode = BSTreeMinimumNode( pNode->m_pRight );

// Если родителем найденного узла не является сам удаляемый узел,

// необходимо отделить его от текущего узла-родителя.
if( pNextNode->m_pParent != pNode )

{

// У него точно нет левого поддерева, иначе бы он не был минимальным.

// Подменяем его правым поддеревом (возможно пустым).

BSTreeTransplant( _tree, pNextNode, pNextNode->m_pRight );

// Сцепляем выбранный узел с правым поддеревом удаляемого узла

pNextNode->m_pRight = pNode->m_pRight;

pNextNode->m_pRight->m_pParent = pNextNode;

}

// Сцепляем выбранный узел с родительским узлом удаляемого узла

BSTreeTransplant( _tree, pNode, pNextNode );

// Сцепляем выбранный узел с левым поддеревом удаляемого узла

pNextNode->m_pLeft = pNode->m_pLeft;

pNextNode->m_pLeft->m_pParent = pNextNode;

}

// Удаляем указанный объект-узел

deletepNode;

}

Тестовая программа

Проверим работу реализованного BST при помощи несложной тестовой программы:

#include "bstree.hpp"

#include <cassert>

#include <iostream>

// Функция обратного вызова для симметричного обхода: печатает ключ в узле

voidprintNode ( constBSTree::Node & _node )

{

std::cout << _node.m_key << ' ';

}

intmain ()

{

// Создаем объект-BST

BSTree * pTree = BSTreeCreate();

// Определяем последовательность ключей для вставки

intkeys[] = { 5, 2, 7, 3, 9, 0, 1, 4, 6, 8 };

intnKeys = sizeof( keys ) / sizeof( int);

// Вставляем ключи в BST в определенном выше порядке

for( inti = 0; i < nKeys; i++ )

BSTreeInsertKey( * pTree, keys[ i ] );

// Каждый из вставленных ключей точно находится в дереве

for( inti = 0; i < nKeys; i++ )

assert( BSTreeHasKey( * pTree, keys[ i ] ) );

// Сопоставляем минимальный и максимальный ключи с ожидаемыми

assert( BSTreeMinimum( * pTree ) == 0 );

assert( BSTreeMaximum( * pTree ) == 9 );

// Выполняем симметричных обход с распечаткой ключей на консоли

BSTreeSymmetricWalk( * pTree, & printNode );

std::cout << std::endl;

// Тестируем удаление ключей

for( inti = 0; i < nKeys; i++ )

{

// Удаляем очередной ключ

BSTreeDeleteKey( * pTree, keys[ i ] );

// После удаления ключ не должен быть представлен во множестве

assert( ! BSTreeHasKey( * pTree, keys[ i ] ) );

// Другие, еще не удаленные ключи, должны остаться во множестве

for( intk = i + 1; k < nKeys; k++ )

assert( BSTreeHasKey( * pTree, keys[ k ] ) );

}

// Уничтожаем объект-BST

BSTreeDestroy( pTree );

}

При вызове данной программы, убеждаемся в упорядоченности вывода ключей при обходе: