Основные сведения о деревьях
Дерево - это математическая абстракция, состоящая из совокупности вершин, называемых узлами, и соединяющих их дуг, называемых ребрами, при этом существует не более одного ребра, соединяющего любую пару узлов, и отсутствуют циклы.
Дерево является частным случаем понятия графа, и имеет широкое распространение в дискретной математике и информатике. В практических задачах часто встречаются древовидные структуры, например:
· каталоги и файлы на диске;
· разделы и главы в книге;
· факультеты и кафедры в университете;
· области и районы в государстве.
Пустое дерево - дерево, не содержащее ни одной вершины.
Каждый узел дерева имеет не более одного узла-родителя и может иметь несколько узлов-потомков, или дочерних узлов. В приведенном ниже примере для узлов B, C и D узел A является родителем, а они для него - потомками. В свою очередь потомками узла B являются узлы E и F, для которых узел B является родителем. Узел G является потомком узла C, для него узел C является родителем.
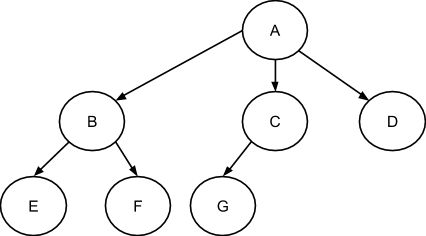
Корень дерева - это узел верхнего уровня, не являющийся потомком ни одного из других узлов. У непустого дерева может быть только один корень. В данном примере корнем является узел A.
Узлы, не имеющие потомков, называются листьями. В приведенном примере листьями являются узлы D, E, F и G.
Узлы-потомки, обладающие общим узлом-родителем, называются братскими. В данном примере братскими между собой являются узлы B, C, D (общий родитель - узел A), узлы E и F (общий родитель - узел B).
Совокупность узлов и соединяющих их ребер, начинающаяся от узла-потомка с точки зрения родителя, называется поддеревом. Например, с точки зрения узла A имеется 3 поддерева:
· поддерево, состоящее из узлов B, E, F
· поддерево, состоящее из улов C и G
· поддерево, состоящее из единственного узла D.
Путем в дереве называется последовательность ребер, соединяющая два связанных узла. Существует не более одного пути между любыми двумя узлами дерева (0 либо 1).
Для любого некорневого узла всегда существует путь до корня. Длина пути от некоторого выбранного узла до корневого, т.е. количество участвующих в пути узлов, называется высотой узла. В частности, высота узла A равна 1, высота узлов B, C и D равна 2, а высота узлов E, F и G равна 3.
Наибольшая высота соответствует наиболее отдаленным от корня узлам-листам, и называется высотой дерева. В примере наибольшая высота узла равна 3, отсюда высота дерева также равна 3.
Дерево, у которого среди всех нелистовых узлов имеется не более N потомков на один узел-родитель, называется N-арным деревом. В таком дереве допускается, что каждый узел имеет от 0 до N узлов-потомков. Приведенный пример представляет собой N-арное дерево с кратностью 3, поскольку наиболее разветвленный узел A имеет 3 узла-потомка.
Если для каждого узла-родителя имеет значение порядок перечисления соответствующих ему узлов-потомков, такое дерево называется упорядоченным. В противном случае, когда порядок перечисления дочерних узлов может быть любым, дерево является неупорядоченным.
Особый случай представляют собой бинарные, или двоичные, деревья. Бинарное дерево - это частный случай упорядоченного N-арного дерева, у которого N=2. Для каждого узла-родителя бинарного дерева поддеревья, образуемые первым и вторым узлами, называются левым и правым поддеревом соответственно.
Также как для элементов связных списков, с узлами деревьев могут быть ассоциированы произвольные данные-значения, иногда в литературе называемые метками узлов.
Обход деревьев
Наиболее часто применяемой операцией на деревьях является обход - перечисление узлов дерева в некотором строго определенном порядке с совершением некоторого полезного действия для каждого из узлов.
При прямом обходе сначала посещается узел-родитель, а затем первое и все последующие поддеревья. Прямой обход характерен многим рекурсивным алгоритмам на древовидных структурах, когда действие сначала применяется к узлу-родителю, а затем ко всем узлам-потомкам. Для приведенного выше примера прямой обход перечислит узлы в таком порядке:
A B E F C G D
При обратном обходе сначала посещаются все поддеревья слева направо, а затем узел-родитель. Такой обход характерен задачам, в которых некоторые вычисления сначала применяются к узлам-потомкам, а их результаты используются на уровне узлов-родителей для получения некоторого общего результата. Такой обход для рассматриваемого примера перечислит узлы следующим образом:
E F B G C D A
Также на практике применяют симметричный, или поперечный обход, в котором сначала посещается первое поддерево, затем узел-родитель, а затем все остальные поддеревья слева направо. Ниже показано перечисление узлов анализируемого примера при таком виде обхода::
E B F A G C D
Глубина рекурсии при обходе однозначно определяется высотой дерева.
АТД “Дерево”
Абстрактный тип данных “дерево” для реализации основных задач, в частности, задачи обхода, должен предоставлять следующий набор обязательных операций:
| ROOT( T ) : N | Возвращает узел, являющийся корнем дерева |
| LABEL( T, N ) : V | Возвращает данное-метку, ассоциированную с конкретным узлом |
| PARENT ( T, N ) : N | Возвращает узел-родитель по узлу-потомку |
| LEFTMOST_CHILD ( T, N ) : N | Возвращает первый узел-потомок по узлу-родителю |
| RIGHT_SIBLING ( T, N ): N | Возвращает следующий братский узел с тем же узлом-родителем |
Следующим образом мог бы выглядеть заголовочный файл, описывающий интерфейс дерева:
tree.hpp
#ifndef _TREE_HPP_
#define _TREE_HPP_
////////////////////////////////////////////////////////////////////////
// Форвардное объявление структуры дерева
structTree;
// Функция создания дерева, принимает число узлов
Tree * TreeCreate ( int_nNodes );
// Функция уничтожения дерева
voidTreeDestroy ( Tree * _pTree );
////////////////////////////////////////////////////////////////////////
// Вспомогательный тип для меток в узлах
typedef charTreeNodeLabel;
// Запрос метки конкретного узла
TreeNodeLabel TreeGetLabel ( constTree & _tree, int_nodeIndex );
// Установка метки конкретного узла
voidTreeSetLabel ( Tree & _tree, int_nodeIndex, TreeNodeLabel _label );
////////////////////////////////////////////////////////////////////////
// Индекс корневого узла
intTreeGetRootIndex ( constTree & _tree );
// Индекс узла-родителя по индексу узла-потомка
intTreeGetParentIndex ( constTree & _tree, int_nodeIndex );
// Установки индекса узла-родителя по индексу узла-потомка
voidTreeSetParentIndex ( Tree & _tree, int_nodeIndex, int_parentIndex );
// Индекс левого поддерева по индексу узла-родителя
intTreeGetLeftmostChildIndex( constTree & _tree, int_nodeIndex );
// Индекс правого братского узла по индексу левого
intTreeGetRightSiblingIndex ( constTree & _tree, int_nodeIndex );
////////////////////////////////////////////////////////////////////////
// Вспомогательный тип - указатель на функцию посещения узла при обходе
typedef void( * TreeNodeVisitFunction ) ( constTree & _t, int_nodeIndex );
// Прямой обход дерева
voidTreeDirectWalk ( constTree & _t, TreeNodeVisitFunction _f );
// Обратный обход дерева
voidTreeReverseWalk ( constTree & _t, TreeNodeVisitFunction _f );
// Симметричный обход дерева
voidTreeSymmetricWalk ( constTree & _t, TreeNodeVisitFunction _f );
////////////////////////////////////////////////////////////////////////.......
#endif // _TREE_HPP_
Используя такой интерфейс, напишем демонстрационную программу, в которой формируется дерево из примера-рисунка, приведенного выше в начале лекции, а затем обойдем его всеми тремя способами с распечаткой меток узлов.
Для формирования четкого представления о рассматриваемых ниже структурах данных реализации, пронумеруем узлы в соответствии с порядком прямого обхода:
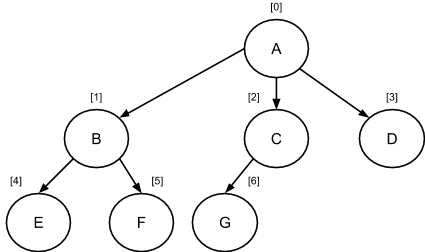
test.cpp
#include "tree.hpp"
#include <iostream>
// Функция посещения узла, печатающая его метку
voidPrintNodeLabel ( constTree & _t, int_nodeIndex )
{
std::cout << TreeGetLabel( _t, _nodeIndex ) << ' ';
}
intmain ()
{
// Создание дерева из 7 узлов
const intNUM_NODES = 7;
Tree * pTree = TreeCreate( NUM_NODES );
// Инициализация меток узлов
for( inti = 0; i < NUM_NODES; i++ )
TreeSetLabel( * pTree, i, 'A' + i );
// Инициализация ребер
TreeSetParentIndex( * pTree, 1, 0 ); // B -> A
TreeSetParentIndex( * pTree, 2, 0 ); // C -> A
TreeSetParentIndex( * pTree, 3, 0 ); // D -> A
TreeSetParentIndex( * pTree, 4, 1 ); // E -> B
TreeSetParentIndex( * pTree, 5, 1 ); // F -> B
TreeSetParentIndex( * pTree, 6, 2 ); // G -> C
// Обход дерева 3 способами с распечаткой значений:
// 1) Прямой
TreeDirectWalk( * pTree, & PrintNodeLabel );
std::cout << std::endl;
// 2) Обратный
TreeReverseWalk( * pTree, & PrintNodeLabel );
std::cout << std::endl;
// 3) Симметричный
TreeSymmetricWalk( * pTree, & PrintNodeLabel );
std::cout << std::endl;
// Уничтожение дерева
TreeDestroy( pTree );
}
Остается лишь предложить способы реализации интерфейса дерева, и программа заработает.
Дата добавления: 2016-01-29; просмотров: 1998;
