Двойное хэширование
Применение базового алгоритма закрытого хэширования иногда приводит к появлению большого количества идущих подряд занятых ячеек. Такие группы называют линейными кластерами. Кластеризация является нежелательным явлением, поскольку замедляет дальнейшую вставку и поиск. Предположим, в сформированную выше таблицу будет добавлена еще одна пара ключ-значение:
| x | y |
Вычислим хэш-код от нового ключа:
| x | h(x)=x%N(N=10) |
Ячейка с индексом 6 уже занята ключом 35 в результате предыдущего разрешения коллизии, несмотря на то, что его хэш-код не равен 6. Соответственно, следуя логике алгоритма, новую пару ключ-значение следует разместить в ближайшей ячейке 9:

Из-за образовавшегося кластера идущих подряд ячеек 5-8, новая пара размещена в ячейке 9, более значительно отстоящей от изначальной 6, на которую указывает хэш-код. Хотя все процедуры хэш-таблицы, такие как поиск, удаление, будут функционировать корректно, это приведет к заметной потере производительности из-за большого количества операций перебора ключей.
Метод двойного хэширования расширяет базовый подход закрытого хэширования и направлен на борьбу с образованием таких кластеров, замедляющих работу таблицы. Суть метода состоит в выборе дополнительной хэш-функции g(x). Для определения позиции размещения ключа xk следует:
- Вычислить начальный хэш-код h(xk) от основной хэш-функции.
- Если соответствующая хэш-коду ячейка еще не занята, разместить ключ в эту ячейку (никаких отличий от базового алгоритма в этом пункте).
- Если ячейка уже занята:
a. Вычислить еще один хэш-код g(xk)от дополнительной хэш-функции.
b. Добавить второй хэш-код к первому, взять остаток от деления полученного кода на размер хэш-таблицы N и вернуться к шагу 2.
Вторая хэш-функция должна обладать следующими свойствами:
- Никогда не возвращать значение 0 (иначе алгоритм зациклится).
- Не должна зависеть от основной хэш-функции (иначе не будет эффекта).
Такой подход существенно уменьшает вероятность формирования кластеров и уменьшает количество коллизий.
Например, пусть в качестве второй хэш-функции будет использоваться следующая:
g(x)=x % 7+1
Ниже приведены значения обеих хэш-функций для рассмотренных в предыдущем примере ключей:
| x | h(x)=x%N(N=10) | g(x)= x%7+1 | (h(x)+g(x))%N |
Следуя логике описанного алгоритма двойного хэширования, разместим узлы в таблице по одному:




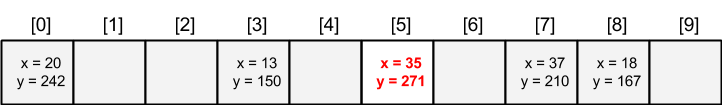
При вставке следующего ключа 45 происходит коллизия, поскольку ячейка 5 уже занята. В этот момент начинает использоваться вторая хэш-функция. Первая дает значение 5, вторая - 4, в сумме 9. Разместим новый элемент в свободную ячейку 9:

Теперь следующий ключ 16, который в базовом алгоритме создавал трудности и помещался далеко от значения первого хэш-кода, с применением двойного хэширования размещается безболезненно:

Для проверки эффективности алгоритма создадим еще одну ситуацию, вызывающую коллизию. Пусть необходимо дополнительно разместить в таблице еще одну пару ключ-значение:
| x | y |
| x | h(x)=x%N(N=10) | g(x)= x%7+1 | (h(x)+g(x))%N |
Хэш-код от основной хэш-функции вызывает коллизию с ключем 45, применяя вторую хэш-функцию и суммируя ее с результатом первой, получим итоговую позицию 1, в которой ячейка не занята::

Конечно, можно подобрать случаи, когда не будет эффективным и двойное хэширование, однако в такой ситуации следует искать решение в виде увеличения размера хэш-таблицы, что с очень высокой вероятностью уменьшит количество коллизий.
Хэш-функции
В качестве ключей в хэш-таблице могут выступать многие типы данных - числа, символы, перечисляемые типы, указатели, строки, структуры, массивы и любые другие пользовательские типы данных. Однако, для успешной организации хэш-таблицы для рассматриваемого типа ключа понадобится отдельная подходящая хэш-функция. Как правило, в качестве хэш-функции не выбирают никаких осмысленных зависимостей, характерных предметной области, поскольку некоторое логичное и понятное человеку преобразование вряд ли будет удовлетворять условию о равномерном распределении всех множеств ключей по области значений хэш-функции.
Предпочтительным является низкоуровневое преобразование байтов памяти, содержащих двоичное представления ключа. Такое универсальное преобразование будет более равномерно распределять все возможные ключи по области значений, а также будет непредсказуемым для человека.
Например, для текстовых строк подойдет следующая функция:
unsigned intHashCodeForString ( const char* _key )
{
unsigned inthashCode = 0;
for( ; *_key; ++_key)
{
charc = *_key;
hashCode = ( hashCode << 5 ) + c;
}
returnhashCode;
}
Каждая буква из строки повлияет на результирующий хэш-код. Сдвиг влево на 5 (умножение на 32) дает удачное распределение для типичных текстов, содержащих различные буквы алфавита.
Если необходима хэш-функция для строк без учета регистра, символы-буквы следует преобразовывать перед суммированием:
unsigned intHashCodeForStringIgnoreCase ( const char* _key )
{
unsigned inthashCode = 0;
for( ; *_key; ++_key)
{
charc = *_key;
if( c >= ‘A’ && c <= ‘Z’ )
c = c - ‘A’ + ‘a’;
hashCode = ( hashCode << 5 ) + c;
}
returnhashCode;
}
Для массивов двоичных данных (абсолютно любой объект в памяти можно интерпретировать как последовательность байт в памяти), можно предложить различные функции с использованием операций сдвига, исключающего ИЛИ и других операций с битами, обеспечивающих равновероятное перемешивание всех бит ключей. Например:
unsigned inthashCodeForBinarySequence ( unsigned char* bytes, size_tlength )
{
unsigned intresult = 0;
for( size_t i = 0; i < length; i++ )
result = result ^ ( ( bytes[i] >> i ) + ( result << 6 ) + ( result >> 2 ) );
returnresult;
}
Возможны и другие варианты для универсальной хэш-функции. Как было уже сказано, важна не форма конкретной функции, а выполнение необходимых для работы хэш-таблицы свойств - повторяемости результата для одинаковых ключей и равномерного распределения ключей по области значений хэш-функции.
В криптографии, где также применяются хэш-функции, существуют популярные алгоритмы для хэширования двоичных данных, обладающие различными свойствами. Например - семейства SHA (Secure Hash Algorithm) и MD (Message Digest Algorithm), имеющие широкое распространение. Они предназначены, в первую очередь, для преобразования больших двоичных файлов в короткие блоки-подписи (160 и 128 бит соответственно), которые можно использовать, например, для сверки подлинности содержимого файла с образцом. В частности, функция MD5 широко используется в программировании для проверки паролей учетных записей пользователей. Такие алгоритмы также можно использовать для организации работы хэш-таблиц, однако такой подход нельзя назвать рациональным для общего случая - криптографические хэш-функции намного более сложны и вычисляются существенно дольше, по сравнению с рассмотренными более простыми аналогами.
Дата добавления: 2016-01-29; просмотров: 6374;
