Уравнение Шредингера
Волны материи
Итак, снова дискретность, таинственные целые числа. В классическойфизике они появлялись в явлениях интерференции (номера максимумови минимумов) и в стоячих волнах (число узлов на закрепленных стру-нах). Луи де Бройль в 1923 г. выдвинул фундаментальную гипотезу:корпускулярно-волновой дуализм(с которым мы встретились на при-мере фотона) насамом деле присущ всем микрочастицам.Фотону мыбыли вынуждены приписать импульс р =h/ 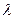 .Долгое время уделялосьвнимание только его волновым свойствам, а в XX веке восстановили вправах и корпускулярные. С электроном получилось наоборот: лишь деБройль разглядел в нем колебания с длиной волны
.Долгое время уделялосьвнимание только его волновым свойствам, а в XX веке восстановили вправах и корпускулярные. С электроном получилось наоборот: лишь деБройль разглядел в нем колебания с длиной волны 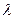 . Условие кван-тования Бора рR =пhполучило простую интерпретацию. Оно сталоусловием того, чтобы на длине стационарной орбиты уложилось целоечисло длин волн: 2
. Условие кван-тования Бора рR =пhполучило простую интерпретацию. Оно сталоусловием того, чтобы на длине стационарной орбиты уложилось целоечисло длин волн: 2 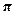 R= п
R= п 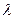 (аналогия с обоями: если по периметрукомнаты укладывается целое число периодов рисунка на обоях, то придальнейшем обклеивании рисунок воспроизводится на тех же местах ---своего рода стационарность). Отсюда вытекает соотношение
(аналогия с обоями: если по периметрукомнаты укладывается целое число периодов рисунка на обоях, то придальнейшем обклеивании рисунок воспроизводится на тех же местах ---своего рода стационарность). Отсюда вытекает соотношение 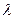 = h/р.Сравнивая с выражением , видим, что получилась общая формуладля фотонов и электронов (и любых других частиц).
= h/р.Сравнивая с выражением , видим, что получилась общая формуладля фотонов и электронов (и любых других частиц).
Гипотеза де Бройля подтверждена экспериментами Дэвиссона и Джер-мера (отражение от кристаллических плоскостей) и Томсона (дифракцияна фольге). Красив и поучителен опыт В. А. Фабриканта (1949 г.) --- ди-фракция одиночных электронов, доказывающая, что волновые свойстваприсущи не коллективу электронов, но каждому в отдельности. И в тоже время электрон --- частица с зарядом и массой.
29.2. Волны материи
115
Вопрос, долго волновавший физиков: что такое микрочастица? Волнаили корпускула? Здесь налицо некорректная постановка вопроса, под-разумевающая альтернативу. Надо ``или'' заменить на ``и'': электрони волна, и частица. Если задать этот вопрос природе с помощью при-бора, то получим ответ, соответствующий прибору: для волнового при-бора (например, дифракционная решетка) ответ будет ``волна'', для кор-пускулярного (скажем, счетчик) --- ``частица''. Неоднозначность ответаотражает двойственность природы частиц или, точнее, узость нашегоальтернативного мышления, допускающего лишь одну из этих возмож-ностей. Это --- новые для нас объекты, квантовые русалки и кентаврымикромира, которых невозможно разделить на людей и животных. Вэтом смысле микрообъект --- ни волна, ни частица и ни их симбиоз. Это--- новое качество, которое мы количественно отражаем в формуле деБройля
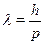
связывающей волновые и корпускулярные проявления свойств единогообъекта. В экспериментах с ускоренными частицами их длина волныде Бройля играет ту же роль, что и длина волны видимого света, опре-деляющая разрешающую силу микроскопа. Ускорители --- своеобразныемикроскопы микромира, и с их помощью исследуются законы природы намалых расстояниях. Так, на ускорителе в Серпухове длина волны про-тонов составляет примерно 10-17 м, что в 10 млн раз меньше размероватомов.
При решении задач, связанных с длиной волны де Бройля, надо с осто-рожностью применять общую формулу 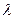 = h/р. Необходимо ясно пони-мать, какое выражение для импульса следует использовать. Например, взадаче может быть задана скорость частицы
= h/р. Необходимо ясно пони-мать, какое выражение для импульса следует использовать. Например, взадаче может быть задана скорость частицы 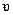 . Если эта скорость многоменьше скорости света с = 2.998 108 м/с, то можно применить класси-ческое соотношение р=тv. (На практике считают, что v
. Если эта скорость многоменьше скорости света с = 2.998 108 м/с, то можно применить класси-ческое соотношение р=тv. (На практике считают, что v 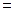 с, еслиотношение v/c ? 0.3, т.е. v2/с2
с, еслиотношение v/c ? 0.3, т.е. v2/с2 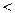 0.1.) Если же это не так, то следуетприменить релятивистское соотношение между импульсом частицы иее скоростью:
0.1.) Если же это не так, то следуетприменить релятивистское соотношение между импульсом частицы иее скоростью:
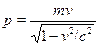
В задаче может быть задана не скорость частицы, а ее кинетическаяэнергия Еk. Критерием применимости классических формул являетсямалость кинетической энергии по сравнению с энергией покоя частицы
Глава 29. Волновые свойства микрочастиц
Ео=тс2.Если условие Ек 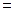 тс2 выполняется (что, как нетрудно ви-деть, эквивалентно условию v
тс2 выполняется (что, как нетрудно ви-деть, эквивалентно условию v 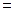 c ), то для нахождения импульса можновоспользоваться формулами классической механики
c ), то для нахождения импульса можновоспользоваться формулами классической механики
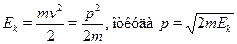
Если же кинетическая энергия частицы не мала по сравнению с энергиейпокоя (тем более, превышает ее), то следует использовать релятивист-ские формулы. В теории относительности выводится общее соотношениемежду полной энергией частицы Е и ее импульсом, которое уже встре-чалось выше :
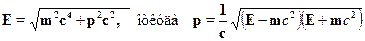 .
.
Кинетическая энергия Ек равна разности между полной энергией и энер-гией покоя: Ек=Е---тс2, так что для импульса получаем
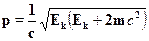
Наконец, удобно переписать это выражение так, чтобы под знаком ква-дратного корня стояли безразмерные величины:
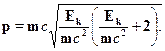
Нетрудно убедиться, что при Ек 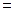 тс2 формула действительно пе-реходит в классическое выражение р=
тс2 формула действительно пе-реходит в классическое выражение р= 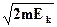 . Традиционные единицыэнергии (Дж) оказываются неудобными в микромире. Поэтому физикипредпочитают пользоваться несистемными единицами --- электронволь-том (эВ) и его производными (1 кэВ = 103 эВ, 1 МэВ = 10б эВ, 1 ГэВ =109 эВ и т.п.).
. Традиционные единицыэнергии (Дж) оказываются неудобными в микромире. Поэтому физикипредпочитают пользоваться несистемными единицами --- электронволь-том (эВ) и его производными (1 кэВ = 103 эВ, 1 МэВ = 10б эВ, 1 ГэВ =109 эВ и т.п.).
Электронвольт --- это энергия, приобретаемая электроном при прохо-ждении разности потенциалов 1 В: Е=еV. Так как заряд электронаравен е = 1.602 10-19 Кл, то 1 эВ = 1.602 10-19 Дж. Поскольку у наспоявилась энергия покоя, приведем ее численные значения для электронаи протона вместе с массами этих частиц. Заодно укажем численные зна-чения постоянной Планка, выраженной в эВ с:
h= 4.136 10-15 эВ с,
29.2. Волны материи
117
h = 6.582 10``16 эВ с,те= 9.109 10-31 кг,mес2 = 8.187 10-14 Дж = 0.511 МэВ,mр = 1.673 10-27 кг,
трс2 = 1.503 10-10 Дж = 938.3 МэВ.
Наконец, встречаются обратные задачи, когда задана длина волныде Бройля 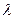 и требуется найти скорость или энергию частицы. Встаетвопрос, как по величине
и требуется найти скорость или энергию частицы. Встаетвопрос, как по величине 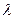 сразу определить, какими формулами сле-дует пользоваться. Представим себе, что мы применяем для нахожде-ния скорости классическую формулу р=тv и, следовательно, получаемv=h/т
сразу определить, какими формулами сле-дует пользоваться. Представим себе, что мы применяем для нахожде-ния скорости классическую формулу р=тv и, следовательно, получаемv=h/т 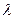 . Критерием справедливости этого результата является ма-лость v по сравнению с с:
. Критерием справедливости этого результата является ма-лость v по сравнению с с:
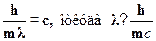
Комбинации 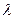 с=h/тси
с=h/тси 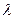 с=h/тс называются комптоновской дли-ной волны частицы. По своему физическому смыслу это --- характерноерасстояние, определяющее область, где уже неприменима нерелятивист-ская квантовая механика. Приведем численные значения этого важногопараметра для электрона и протона:
с=h/тс называются комптоновской дли-ной волны частицы. По своему физическому смыслу это --- характерноерасстояние, определяющее область, где уже неприменима нерелятивист-ская квантовая механика. Приведем численные значения этого важногопараметра для электрона и протона:
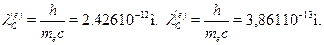
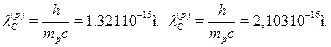

Видно, что чем легче частица, тем больше ее комптоновская длина волны,то есть тем раньше проявятся релятивистские эффекты. Для электронакомптоновская длина волны много меньше характерной длины, опреде-ляющей размеры атома. Это значит, что к атому применима нереляти-вистская квантовая механика. Ядра, состоящие из протонов и нейтронов,имеют размеры порядка 10-14 м, что много больше комптоновской длиныволны протона. Следовательно, к ним также применима эта теория.
Задача 29.18.Определить скорость частицы, у которой длина волныде Бройля в 10 раз меньше комптоновской длины волны 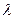 с-
с-
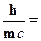 10
10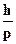
Решение.По условию
Глава 29. Волновые свойства микрочастиц
откуда находим для импульса частицы
р = 10mc.
Так как длина волны де Бройля меньше комптоновской длины волнычастицы, то мы не можем воспользоваться нерелятивистским соотно-шением р = те, которое приведет к несуразному ответу v = 10с (какизвестно, ничто не может двигаться быстрее света). Здесь необходимоприменить релятивистскую формулу связи импульса со скоростью:
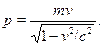
Отсюда вытекает уравнение
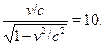
решение которого дает
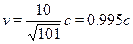
то есть скорость частицы всего на 0.5% меньше скорости света. ¦
• Соотношения неопределенностей
Само наличие у частицы волновых свойств накладывает определенныеограничения на возможность корпускулярного описания ее поведения.Для классической частицы всегда можно указать ее точное положениеи импульс. Для квантового объекта имеем иную ситуацию.
Представим цуг волн пространственной протяженностью  х --- образлокализованного электрона, положение которого известно с точностью
х --- образлокализованного электрона, положение которого известно с точностью  х. Длину волны электрона можно определить, подсчитав число пери-одов на отрезке: N=
х. Длину волны электрона можно определить, подсчитав число пери-одов на отрезке: N=  х/
х/ 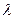 . Какова точность определения
. Какова точность определения 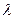 ? Ясно,что для слегка отличающейся длины волны мы получим то же самоезначение N. Неопределенность
? Ясно,что для слегка отличающейся длины волны мы получим то же самоезначение N. Неопределенность 
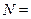
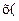
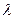
/ 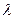 2) в числе узлов, причем измерению доступны лишь
2) в числе узлов, причем измерению доступны лишь  N
N 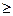 1. Так как р = h/
1. Так как р = h/ 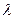 и
и  р = h
р = h 
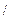
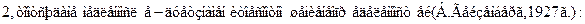
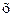
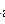
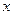
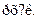
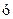
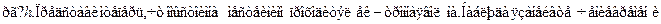
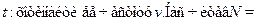
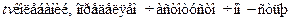
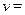
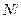
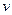 >
> 
 >
> 
 >
> 
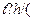 E_ 1
E_ 1  E_ 2
E_ 2 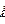
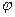
влечет за собой неопределенность ее положения на орбите  х = R
х = R 
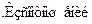
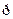 >
> 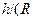
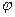
) . Учитываясвязь момента количества движения Lс импульсом (L=Rр), получаем  R=R
R=R  р, откуда следует соотношение неопределенностей
р, откуда следует соотношение неопределенностей
 L
L 
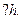
Для массивных объектов правая часть исчезающе мала, что позво-ляет одновременно измерить скорость и положение объекта (областьсправедливости классической механики). В атоме же Бора импульсэлектрона р= h/а, и неопределенность положения оказывается по-рядка размеров орбиты!
• Невозможность достижения минимума потенциальной энергии. При-мер: осциллятор (тело на пружине):
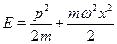
Основное состояние в классической механике: р = 0 , х = 0 . Поэтомувеличина неопределенностей --- порядка самих импульса и коорди-нат:
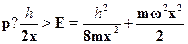
Минимум достигается в точке х = 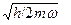 и равен
и равен
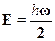
29.3. Соотношения неопределенностей
121
В принципе мы не можем претендовать на точный ответ, хотя в дан-ном случае (то же --- для атома водорода) он действительно точен.Мы получили так называемые нулевые колебания:квантовый осцил-лятор, в отличие от классического, не может оставаться в покое: этопротиворечит соотношению неопределенностей Гейзенберга. Точ-ные расчеты показывают, что формулу Планка для уровней энергииосциллятора надо было бы писать в виде
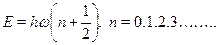
При решении задач на применение соотношения неопределенностейследует иметь в виду, что в основном состоянии в классической фи-зике электрон покоится в точке, соответствующей минимуму потенци-альной энергии. Соотношения неопределенностей не позволяют ему этоделать в квантовой теории, так что электрон должен иметь некоторыйразброс импульсов. Поэтому неопределенность импульса (его отклонениеот классического значения 0) и сам импульс по порядку величины совпа-дают (р  р).Неопределенность координаты электрона, замкнутого вобъеме V, равна по порядку величины линейному размеру этого объема
р).Неопределенность координаты электрона, замкнутого вобъеме V, равна по порядку величины линейному размеру этого объема
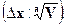
Задача 29.19.Электрон с кинетической энергией 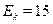 эВ находитсяна металлической пылинке диаметром d= 1 мкм. Оценить относитель-ную неточность
эВ находитсяна металлической пылинке диаметром d= 1 мкм. Оценить относитель-ную неточность 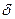 v, с которой может быть определена скорость электрона.
v, с которой может быть определена скорость электрона.
Решение.По условию  х?d/2и
х?d/2и  р?2h/d.Энергия электронамного меньше его энергии покоя, так что можно применять нереляти-вистские соотношения Ек = теv2/2, р=
р?2h/d.Энергия электронамного меньше его энергии покоя, так что можно применять нереляти-вистские соотношения Ек = теv2/2, р= 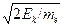 ,
,  р=me
р=me  v,откуда
v,откуда  v?2h/(теd). Для относительной неопределенности скоростиэлектрона получаем
v?2h/(теd). Для относительной неопределенности скоростиэлектрона получаем
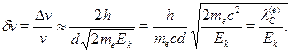
В этом выражении выделены безразмерные множители --- отношениекомптоновской длины волны электрона к диаметру пылинки и отноше-ние энергии покоя электрона к его кинетической энергии. Подставляемчисленные значения:
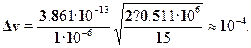
Глава 29. Волновые свойства микрочастиц
Задача 29.20.Среднее время жизни атома в возбужденном состоянии 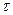 = 10-8 с. При переходе в основное состояние излучается фотон с длинойволны
= 10-8 с. При переходе в основное состояние излучается фотон с длинойволны 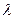 = 0.5 мкм (зеленый цвет). Определить энергию кванта, ширинуи относительную ширину спектральной линии.
= 0.5 мкм (зеленый цвет). Определить энергию кванта, ширинуи относительную ширину спектральной линии.
Решение.Энергия кванта равна
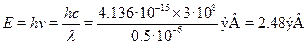
Неопределенность в энергии определяется по соотношению  t
t 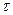 ):
):
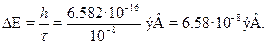
Отсюда
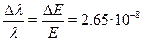
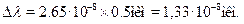
• О границах применимости квантовой механики
Собственно, мы еще с квантовой механикой даже не познакомились, нолишь подошли к ее порогу. Тем не менее, уже сейчас можно дать оценкуобласти, в которой заведомо не будут справедливы выводимые нами со-отношения. Если подходить к микромиру со стороны области примени-мости классической физики, то никаких проблем не возникает. В самомделе, квантовые соотношения вовсе не отменяют классических законов,но уточняют их. В макромире с большими значениями энергий и мо-ментов количества движения квантовая дискретность просто будет неза-метна, так что спокойно можно применять и квантовые, и классическиезаконы. Разница между получаемыми с их помощью количественнымирезультатами будет ничтожно мала, но классические законы проще. Вэтом смысле мы говорим об области, где справедливы законы классиче-ской физики.
Иное дело, когда мы станем продвигаться вглубь микромира. В прин-ципе ясно, что где-то откажут и законы квантовой механики, и ученымпридется придумать какую-то новую теорию. В этом курсе мы будемзаниматься нерелятивистской квантовой механикой, изучающей микро-объекты, движущиеся со скоростями, гораздо меньшими скорости света
29.4. О границах применимости квантовой механики
123
с. Мы встретимся и с релятивистскими объектами (фотонами и др.), нобудем оговаривать такие случаи особо.
Определим теперь область справедливости нерелятивистской кванто-вой механики. Представим себе микрочастицу с массой т. Квантоваянеопределенность  Е ее энергии должна быть много меньше энергиипокоя тс2 (в противном случае квантовые эффекты с необходимостьюбудут релятивистскими, что потребует обобщения теории). Из соотно-шения неопределенностей и условия применимости нерелятивист-ских уравнений
Е ее энергии должна быть много меньше энергиипокоя тс2 (в противном случае квантовые эффекты с необходимостьюбудут релятивистскими, что потребует обобщения теории). Из соотно-шения неопределенностей и условия применимости нерелятивист-ских уравнений  Е
Е 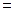 тс2 следует ограничение на интервалы времени:
тс2 следует ограничение на интервалы времени:  t
t 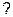 h/mc2. Характерное время tС = h/тс2 является, таким образом,водоразделом между релятивистской и нерелятивистской квантовыми те-ориями. За это время частица может пройти расстояние не большесtс = h/тс. Величина h/тс --- характерное расстояние, на которомпроходит граница между нерелятивистской и релятивистской теориями.Для электрона оно равно 3.86 10-13 м, а для протона --- 2.1 10" 16 м.Соответствующие промежутки времени равны tС = 1.3 10-21 с для элек-трона и tС= 7 10-25 с для протона.
h/mc2. Характерное время tС = h/тс2 является, таким образом,водоразделом между релятивистской и нерелятивистской квантовыми те-ориями. За это время частица может пройти расстояние не большесtс = h/тс. Величина h/тс --- характерное расстояние, на которомпроходит граница между нерелятивистской и релятивистской теориями.Для электрона оно равно 3.86 10-13 м, а для протона --- 2.1 10" 16 м.Соответствующие промежутки времени равны tС = 1.3 10-21 с для элек-трона и tС= 7 10-25 с для протона.
На рис. 29.3 по оси х в логарифмическом масштабе отложены рассто-яния, а по оси у --- скорости. Отмечены области применимости основныхфизических теорий (ОТО --- общая теория относительности, СТО --- спе-циальная теория относительности, КТП --- квантовая теория поля, онаже --- релятивистская квантовая теория, она же --- теория элементарныхчастиц). Штриховкой показаны области применимости теорий, изучав-шихся нами. Правая граница заштрихованной области КМ не означает,что квантовую механику нельзя применять там, где мы привыкли поль-зоваться классической. Просто это делать нецелесообразно.
Обратим внимание, что рисунок ограничен с обеих сторон. Большойвзрыв, в котором родилась наша Вселенная, произошел 15-20 млрд леттому назад. За это время свет преодолел путь порядка 1026 м , что и опре-деляет максимальные возможные расстояния в этом мире. На расстоя-ниях порядка 10-35 м необходимо учитывать силы гравитации, квантоваятеория которых пока не создана. Только очень смелые теоретики реша-ются серьезно обсуждать, что происходит на столь малых расстояниях.Поэтому данная область на рисунке не показана.
Подведем итоги этой главы. Мы пришли к противоречивой картинемикромира. В атоме Бора использовались законы движения по класси-ческой траектории, которые в результате оказались несправедливыми.
Глава 29. Волновые свойства микрочастиц
Рис. 29.3: Диаграмма расстояние-скорость делает наглядными области применимо-сти физических теорий: классической механики, специальной теории относительности(СТО), квантовой механики (КМ), общей теории относительности (ОТО) и квантовойтеории поля (КТП). Границы между различными теориями размыты, так как они не от-рицают друг друга, но развивают и дополняют. Так, КТП, занимающаяся свойствамиэлементарных частиц, родилась при соединении КМ и СТО, а ОТО (она же теориягравитации) --- при распространении СТО и классической механики на область боль-ших расстояний. Точка показывает электрон в атоме, свойства которого, как видно,попадают в сферу действия квантовой механики.
Расчет радиуса орбиты и импульса электрона противоречит волновымидеям де Бройля, из которых мы и выводили эти характеристики. Нако-нец, совершенно непонятно, что же колеблется в пространстве при дви-жении электрона?
Контрольные вопросы
• Что такое спектральные серии?
• Сформулируйте постулаты Бора.
• Какие значения могут принимать радиусы электронных орбит в атоме водородав теории Бора?
4. Какие значения может принимать скорость электрона, находящегося в поле ядрас зарядом +Zе? На основании полученного результата покажите, чтов природене могут существовать ядра с Z 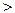 137.
137.
29.4. О границах применимости квантовой механики
125
• Какие значения может принимать энергия электрона в атоме водорода в теорииБора?
• Как теория Бора объясняет спектральные серии?
• В чем сущность гипотезы де Бройля?
• Какова длина волны де Бройля у электрона с кинетической энергией, равной егоэнергии покоя?
• Сформулируйте соотношения неопределенностей Гейзенберга.
• Вообразите мир, в котором постоянная Планка имеет значение h=2000 Дж с.Живя в этом мире, Вы назначаете свидание, которое может состояться, если Вы иВаш партнер окажетесь в одном месте --- скажем, на расстоянии порядка  x 1мдруг от друга. Будет ли у вас возможность спокойно пообщаться на свидании?
x 1мдруг от друга. Будет ли у вас возможность спокойно пообщаться на свидании?
Глава 30
Уравнение Шредингера
Вот мы и подошли к настоящей квантовой механике. Все, что было досих пор это интуитивные полуклассические представления, позво-
Лившие инкорпорировать в классическую физику идеи физики кванто-вой. Но этот уровень знаний недостаточен для расчетов, количествен-ных предсказаний многих явлений. Требуется стройная система, те-ория движения (или распространения) микрочастиц с дуальными (волна-корпускула) свойствами.
• Волна вероятности
Предыдущая глава закончилась констатацией, что мы пока не устано-вили, что именно колеблется при движении электрона. В истории фи-зики такое уже случалось. Когда-то при выводе уравнений электроди-намики Максвелл тоже не знал, что представляют собой описываемыеими колебания и волны, но уравнения оказались верны. Поэтому отло-жим пока вопрос о физической природе волн де Бройля и просто введемнекую ``электронную'' волну, т.е. функцию 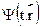 . О ней мы знаем покатолько одно: волновая функция должна описывать результаты опытов,доказывающих волновые свойства электронов (дифракцию и т.п.).
. О ней мы знаем покатолько одно: волновая функция должна описывать результаты опытов,доказывающих волновые свойства электронов (дифракцию и т.п.).
Представим мысленно эксперимент В. А. Фабриканта, в котором элек-троны поочередно направлялись на кристалл, играющий роль дифракци-онной решетки. За кристаллом помещена фотопластинка, на которой вконце концов возникают типичные дифракционные кольца. Из классиче-ской физики известно, какие математические средства описывают такуюкартину: обычное сложение интерферирующих волн, интенсивности ко-торых пропорциональны | 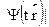 2 .
2 .
Правда, в отличие от обычной волны электрон не делится на части:
30.1. Волна вероятности
127
при прохождении электронов через кристалл каждый из них попадаетв какую-то одну точку на фотопластинке, вызывая почернение именноздесь и нигде больше. В этом проявляются свойства электрона как ча-стицы. Несмотря на одинаковые начальные условия электроны, как по-казал опыт, попадают в разные точки. О данном конкретном электронезаранее неизвестно, в какую именно точку на пластинке он попадет. Вэтом проявляются его волновые свойства. Дифракционная картина воз-никает, когда через кристалл пройдет достаточно много таких электро-нов. Интенсивность почернения пластинки в данной точке пропорцио-нальна числу попавших туда частиц, то есть вероятности попадания.
В классической же физике почернение пластинки определяется интен-сивностью волны, то есть квадратом модуля волновой функции. Выхо-дит, что | 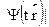 2 пропорционален вероятности обнаружить электрон вточке
2 пропорционален вероятности обнаружить электрон вточке 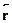 в момент времени t. Волна де Бройля --- это волна вероятно-сти! Отдельный акт взаимодействия электрона с кристаллом остаетсяотдельным актом (электрон-частица), но результат его можно предска-зать только вероятностно, статистически (электрон-волна). В этом ---смысл корпускулярно-волнового дуализма. Квантовая механика созданав 1925-27 гг. В. Гейзенбергом и Э. Шредингером; вероятностная ин-терпретация волновой функции дана чуть позже в работах М. Борна ишколы Н. Бора.
в момент времени t. Волна де Бройля --- это волна вероятно-сти! Отдельный акт взаимодействия электрона с кристаллом остаетсяотдельным актом (электрон-частица), но результат его можно предска-зать только вероятностно, статистически (электрон-волна). В этом ---смысл корпускулярно-волнового дуализма. Квантовая механика созданав 1925-27 гг. В. Гейзенбергом и Э. Шредингером; вероятностная ин-терпретация волновой функции дана чуть позже в работах М. Борна ишколы Н. Бора.
Итак, вероятность найти электрон в точке 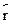 должна быть пропорци-ональна |
должна быть пропорци-ональна | 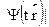 2. Но вероятность обнаружить электрон точно в данномместе исчезающе мала; имеет смысл говорить лишь о его попадании вмалый объем dV, окружающий эту точку. Ясно, что вероятность dWобнаружить там электрон пропорциональна величине объема. Поэтомудля вероятности имеем
2. Но вероятность обнаружить электрон точно в данномместе исчезающе мала; имеет смысл говорить лишь о его попадании вмалый объем dV, окружающий эту точку. Ясно, что вероятность dWобнаружить там электрон пропорциональна величине объема. Поэтомудля вероятности имеем
Иными словами, | 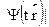 2--- плотность вероятности найти частицу вточке с координатой
2--- плотность вероятности найти частицу вточке с координатой 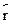 . Вероятность W(v)найти частицу в каком-токонечном объеме v вычисляется с помощью сложения вероятностей, т.е.интегрированием
. Вероятность W(v)найти частицу в каком-токонечном объеме v вычисляется с помощью сложения вероятностей, т.е.интегрированием
Интегрирование в ведется по объему v (в случае одномерного дви-жения --- по отрезку). Полная вероятность найти частицу хоть где-нибудь в пространстве должна быть равна единице. Отсюда --- так на-
dW= | 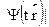 2dV.
2dV.
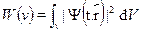
Глава 30. Уравнение Шредингера
зываемое условие нормировки волновой функции: такой же интеграл повсему пространству равен единице, т.е.
Замечание: выполнение этого условия возможно для тех задач, в кото-рых классическая частица движется в ограниченной области простран-ства (финитное движение). Для других движений условие нормировкиусложняется.
Наблюдаемые физические величины должны описываться действитель-ными числами и функциями. Соответственно, мы представляли класси-ческие волны (звуковые, электромагнитные) в виде 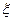 = A0cos(
= A0cos( 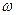 t-
t- 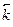 r
r 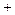
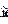
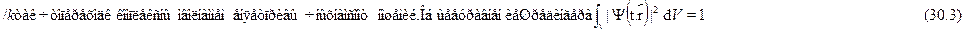
e-i 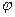 = соs
= соs 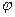 ---i sin
---i sin 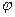 ,
,
где i= 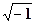 --- мнимая единица. Тогда ту же волну можно было быпредставить в виде действительной части выражения:
--- мнимая единица. Тогда ту же волну можно было быпредставить в виде действительной части выражения:
Волновая функция является главным объектом изучения в квантовой ме-ханике. Говоря о каком-то состоянии в классической физике, мы подра-зумевали, что в момент времени t= 0 частица имела некие положение и
30.2. Общее уравнение Шредингера
129
скорость (импульс), а дальнейшая ее судьба предопределена уравнениямидвижения Ньютона.
Состояние в квантовой механике имеет иной смысл: в момент времениt = 0 задана волновая функция, изменение которой регулируется пока неизвестным нам уравнением (Шредингера). В этом смысле теперь пони-мается причинность: в классике --- точные предсказания положений искоростей, в квантовой механике --- предсказания состояний (волновыхфункций). Уравнения новой физики (в данном случае --- уравнение Шре-дингера) никогда не выводятся логически из прежних принципов (иначеэто будет не новая теория, а следствие старой). Но квантовомеханическоеуравнение должно иметь некие классические корни, поскольку классиче-ская механика хороша в области своей применимости. Далее мы приве-дем не вывод, но наводящие соображения.
Свободной частице соответствует волна де Бройля, которую мы запи-сываем в виде классической плоской волны:
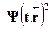 =
= 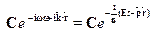 .
.
где модуль волнового вектора к связан с длиной волны соотношениемk =2 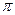 /
/ 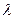 , а С --- амплитуда. Мы использовали уже известную связьэнергии и импульса частицы с частотой и длиной волны де Бройля. Ис-комое уравнение для волновой функции не должно содержать Е и р, таккак это --- характеристики конкретного состояния частицы. Попробуемнайти операции над волновой функцией свободной частицы, позволяю-щие исключить параметры Е и
, а С --- амплитуда. Мы использовали уже известную связьэнергии и импульса частицы с частотой и длиной волны де Бройля. Ис-комое уравнение для волновой функции не должно содержать Е и р, таккак это --- характеристики конкретного состояния частицы. Попробуемнайти операции над волновой функцией свободной частицы, позволяю-щие исключить параметры Е и 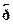 . Имеем для производной по времени
. Имеем для производной по времени
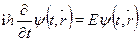
и по пространственной координате х
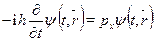 .
.
Такие же уравнения возникнут при дифференцировании по у и z. Повто-ряя дифференцирование по координатам, получаем:
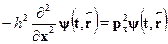
Складывая с аналогичными уравнениями для вторых производных
по у и 2, приходим к соотношению:
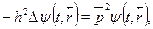
Глава 30. Уравнение Шредингера
где знаком  обозначен оператор Лапласа:
обозначен оператор Лапласа:
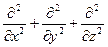
В этом месте возникает различие между релятивистским и нереля-тивистским случаями. Квантовая механика --- нерелятивистская те-ория., в которой Е= 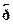 2/2m. Это классическое соотношение позволяетсвязать дифференцирование по времени в с дифференцированиемпо пространственным координатам в и тем самым исключить изуравнения зависимость от энергии и импульса частицы:
2/2m. Это классическое соотношение позволяетсвязать дифференцирование по времени в с дифференцированиемпо пространственным координатам в и тем самым исключить изуравнения зависимость от энергии и импульса частицы:
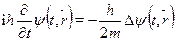
Это уравнение вполне бы нас устроило, но написано оно пока толькодля свободной частицы. Легко понять, как должно выглядеть уравнениедля системы с постоянным значением U0 потенциальной энергии. Полнаяэнергия равна сумме
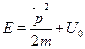
так что получаем
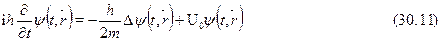
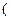
В случае частицы, находящейся в произвольном потенциальном полевблизи точки 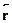 потенциальную энергию можно считать постоянной ве-личиной U(
потенциальную энергию можно считать постоянной ве-личиной U( 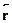 ), так что искомое обобщение почти с очевидностью следуетиз уравнения :
), так что искомое обобщение почти с очевидностью следуетиз уравнения :
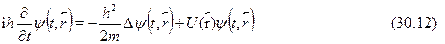
Это и есть основное уравнение квантовой механики --- знаменитоеуравнение Шредингера. Подчеркнем еще раз, что вывести его строгоневозможно, но можно угадать, исходя из наводящих соображений. Соот-ветствие уравнения и его следствий физической реальности проверяетсяэкспериментально. Подчеркнем некоторые свойства :
Уравнение Шредингера по сути есть аналог классического соотноше-ния между полной энергией Е частицы и ее кинетической энергией 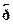 2/2т. Для свободной частицы они совпадают. При наличии потен-циального поля это соотношение принимает вид Е=
2/2т. Для свободной частицы они совпадают. При наличии потен-циального поля это соотношение принимает вид Е= 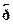 2/2т+U(
2/2т+U( 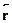 ).
).
30.3. Операторы, симметрия и законы сохранения
131
Мы уже знаем, что полной энергии соответствует производная по t,компонентам импульса --- производные по x, у, z, а кинетическойэнергии --- вторые производные по пространственным координатам,поскольку импульс входит в нее во второй степени. Классическойпотенциальной энергии, как мы видим, в квантовой механике соот-ветствует обычное произведение U( 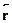 ) на волновую функцию.
) на волновую функцию.
Заметим, что уравнение Шредингера линейно по искомой волновой функ-ции. Отсюда сразу же вытекает, что
• если  ?
? 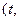 r
r 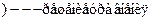 ?
?

(t, 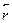 )--- также егорешение при любой константе А. Следовательно, подбором постоян-ной А можно добиться выполнения условия нормировки ;
)--- также егорешение при любой константе А. Следовательно, подбором постоян-ной А можно добиться выполнения условия нормировки ;
• если  ?
? 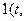 r
r 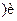 ?
?

2 (t, 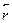 )--- решения уравнения Шредингера, то линей-ная комбинация A1
)--- решения уравнения Шредингера, то линей-ная комбинация A1  ?
? 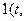 r
r 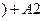 ?
?

2 (t, 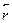 ) --- также его решение (принципсуперпозиции, т.е. основа явления интерференции).
) --- также его решение (принципсуперпозиции, т.е. основа явления интерференции).
• Операторы, симметрия и законы сохранения
Итак, состояние электрона описывается теперь волновой функцией  ?
? 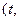 r
r 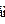 ?
?

(t, 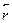 ). Из уравнения Шредингера видно, чтооно воспроизводит связь Е=Т+U полной энергии Е с кинетической Ти потенциальной U, но классические величины заменены на операторы,действующие на волновую функцию Ф. Будем обозначать оператор темже символом, что и классическую величину, снабжая его для отличияшляпкой. Тогда уравнение Шредингера можно записать в опера-торной форме, в которой отчетливо видна его связь с энергетическимисоотношениями классической физики:
). Из уравнения Шредингера видно, чтооно воспроизводит связь Е=Т+U полной энергии Е с кинетической Ти потенциальной U, но классические величины заменены на операторы,действующие на волновую функцию Ф. Будем обозначать оператор темже символом, что и классическую величину, снабжая его для отличияшляпкой. Тогда уравнение Шредингера можно записать в опера-торной форме, в которой отчетливо видна его связь с энергетическимисоотношениями классической физики:
E  ?
? 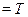 ?
?

+U  ?
? 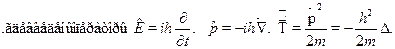
Глава 30. Уравнение Шредингера
Здесь 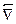 --- оператор градиента с компонентами:
--- оператор градиента с компонентами:
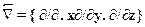
квадрат которого дает оператор Лапласа  . Оператор координаты
. Оператор координаты  сводится к простому умножению
сводится к простому умножению  ?
?  r
r  r
r  r
r 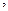 p
p 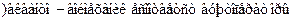 r
r 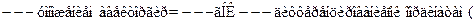 р
р 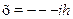 ?
?

/  ?
? 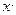 p
p 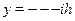 ?
?

/  ?
? 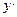 p
p 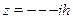 ?
?

/  ?
? 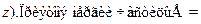 р
р 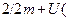 r
r 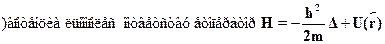
В этих обозначениях уравнение Шредингера имеет вид:
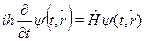
Оператор полной энергии 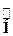 называется гамильтонианом (аналог функ-ции Гамильтона в теоретической механике).
называется гамильтонианом (аналог функ-ции Гамильтона в теоретической механике).
Очень важно! В классической механике законы сохранениясвязаны с симметрией системы: энергия --- с трансляцией (сдви-гом) времени t>t+ 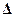 t, импульс --- с трансляцией пространства
t, импульс --- с трансляцией пространства 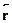 >
> 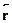 +
+ 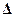 г
г 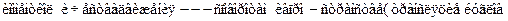
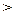
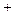

).
Трансляцию какой-то обобщенной координаты производит оператордифференцирования по этой координате. Например, для бесконечно ма-лой трансляции q>q+  q имеем по определению производной
q имеем по определению производной
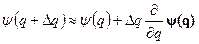
Поэтому не случайно в квантовой механике полной энергии соответствует  ?
? 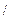 ?
?

t, а импульсу --- градиент 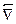 . Аналогично: оператор проекции мо-мента количества движения на какую-то ось z пропорционален оператору
. Аналогично: оператор проекции мо-мента количества движения на какую-то ось z пропорционален оператору
30.4. Стационарное уравнение Шредингера
133
дифференцирования  ?
? 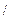 ?
?

рпо углу поворота вокруг этой оси:
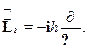
• Стационарное уравнение Шредингера
В теории операторов важную роль играют так называемые собствен-ные состоянияоператоров. Это такие состояния, которые при действииданного оператора меняются тривиальным образом: умножаются на не-которое число. Это число называется собственным значениемданногооператора, соответствующим данному собственному состоянию. Чтобынайти собственные состояния и собственные значения какого-то опера-тора Анадо решить уравнение
А  ?
? 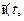 r
r 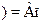 ?
?

п(t, 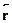 ),
),
где индекс потличает одно решение от другого. Набор величин Ап,тоесть набор собственных значений оператора А, определяет его свойства.
Пример: операция поворота вокруг некоторой оси 2. Роль состоя-ний играют здесь обычные радиус-векторы. Очевидно, что при поворотевсе векторы меняются, кроме параллельных оси. Это и есть собствен-ные векторы оператора поворота вокруг оси 2, причем соответствующеесобственное значение равно единице. Аналогичны выводы для поворотавокруг осей ж и у. Произвольный поворот можно получить комбина-цией этих трех поворотов. Соответственно, любой радиус-вектор можнопредставить как линейную комбинацию трех собственных векторов г,] ,к.Ситуация с другими операторами по сути ничем не отличается от опи-санной: зная набор собственных состояний любое другое состо-
яние  ?
? 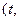 r
r 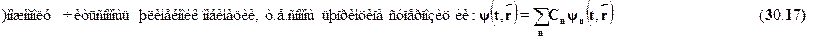
Связь математики с физикой реализуется в следующем правиле:
Правило 2 Измерение некой физической величины А всегда дает лишьодно из собственных значений Ап соответствующего ей оператора А.Вероятность получить при измерении именно значение Ап определя-ется состоянием системы (а именно, квадратом модуля \ Сп\ 2 соот-ветствующего коэффициента в разложении ).
Глава 30. Уравнение Шредингера
Следствие: в собственном состоянии  ?
? 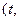 r
r 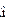 ?
?

е оператора полнойэнергии. Уравнение, согласно сказанному, имеет вид:
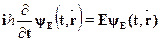
откуда следует решение
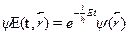
Мы получили общий вид состояния, в котором энергия имеет опреде-ленное значение. Такие состояния называются стационарными. Есте-ственно, пока невозможно сказать, чему равна энергия стационарногосостояния, поскольку мы еще не указали рассматриваемую физическуюсистему. В уравнении стоит некая функция  ?
? 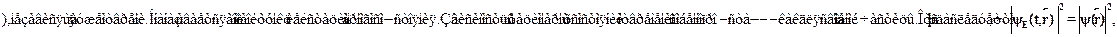
т.е. в стационарном состоянии плотность вероятности не зависит от вре-мени. В этом смысле и следует понимать название ``стационарное''. Под-ставляя решение в общее уравнение Шредингера , получимт.н. стационарное уравнение Шредингера, т.е. уравнение для  ?
? 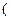 r
r 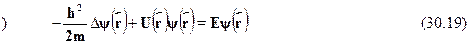
Подчеркнем: это --- уравнение для состояний с определенной энергиейЕ. В операторных обозначениях оно имеет вид 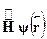 = E
= E 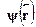 , то естьпредставляет собой уравнение для собственных состояний гамильтони-ана. Задавая тот или иной вид потенциальной энергии, мы конкретизи-руем систему и получаем стационарное уравнение Шредингера, решениякоторого и описывают квантовые свойства системы.
, то естьпредставляет собой уравнение для собственных состояний гамильтони-ана. Задавая тот или иной вид потенциальной энергии, мы конкретизи-руем систему и получаем стационарное уравнение Шредингера, решениякоторого и описывают квантовые свойства системы.
Не следует думать, что система может быть только в стационарномсостоянии. Возьмем характерный пример: пусть 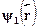 и
и  --- два не-ких стационарных состояния какой-то системы с разными энергиями E1\
--- два не-ких стационарных состояния какой-то системы с разными энергиями E1\
30.5. Уравнение Шредингера для простейших систем
135
и Е2. Предположим, что в начальный момент времени волновая функциясистемы является симметричной суперпозицией этих состояний:
Вопрос: что будет с системой в произвольный момент t
Зная, что справедлив принцип суперпозиции и что зависимость соб-ственных состояний от времени определяется соотношениями типа ,можно сразу же написать волновую функцию:
Плотность вероятности такого состояния зависит от времени! Введемобозначения для средней энергии Е=( 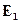 +Е2)/2 и частоты перехода
+Е2)/2 и частоты перехода 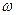 =(
=( 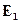 ---Е2)/h. Тогда
---Е2)/h. Тогда 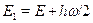 .
. 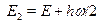 , и легко получаем
, и легко получаем
вместо :
Видно, что в момент t = 0 система находится в симметричном со-стоянии, к моменту времени t = 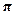 /
/ 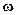 она перейдет в антисимметричноесостояние, а в момент t = 2
она перейдет в антисимметричноесостояние, а в момент t = 2 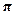 /
/ 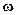 --- снова вернется в симметричное со-стояние. Следовательно, система осциллирует между симметричным иантисимметричным состояниями с круговой частотой
--- снова вернется в симметричное со-стояние. Следовательно, система осциллирует между симметричным иантисимметричным состояниями с круговой частотой 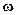 . Здесь усматри-вается аналогия с классической физикой: в рассмотренной ранее системесвязанных осцилляторов (см. Ч. 4, раздел 24.4.3) возникают похожиесобственные колебания (нормальные моды) и биения.
. Здесь усматри-вается аналогия с классической физикой: в рассмотренной ранее системесвязанных осцилляторов (см. Ч. 4, раздел 24.4.3) возникают похожиесобственные колебания (нормальные моды) и биения.
• Уравнение Шредингера для простейших систем
Дата добавления: 2016-01-26; просмотров: 1176;
