Трехмерный осциллятор
Эта задача является обобщением предыдущей. Как и для трехмернойпотенциальной ямы с бесконечно высокими стенками, волновая функцияпредставляется в виде произведения волновых функций одномерных ос-цилляторов, колеблющихся независимо вдоль осей х,у,z. Так, волноваяфункция основного состояния имеет вид:
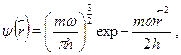
а уровни энергии трехмерного осциллятора описываются формулой
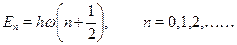
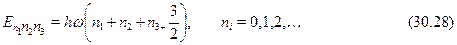
30.6. Принцип соответствия Бора
141
В отличие от одномерного осциллятора состояние определяется значе-нием трех квантовых чисел Легко понять, что все возбужден-
ные состояния должны быть вырожденными.
• Принцип соответствия Бора
Н. Бор на заре квантовой механики поставил вопрос о ее соотношениис классической. Обычные в нашем мире значения энергии велики посравнению с характерной энергией основного состояния и расщеплениемуровней: с высокой лестницы не различаем ступенек. Более научно: прибольших квантовых числах(высоколежащих уровнях) должны воспро-изводиться классические результаты. Покажем это на примере атомаводорода.
В главе 1 в разделе об атоме Бора было получено классическое выра-жение для скорости электрона на орбите радиусом R:
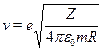
Отсюда легко получить классическую частоту вращения электрона:
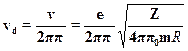
Кроме того, было найдено классическое выражение для энергии элек-трона на орбите:
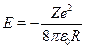
позволяющее выразить радиус орбиты через энергию электрона:
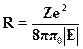
Подставляя это выражение в формулу для классической частоты враще-ния цс/, получаем
Именно на этой частоте ожидается излучение электрона в классическойтеории.
Глава 30. Уравнение Шредингера
Кроме того, в том же разделе было выведено выражение для энергииуровня с номером п:
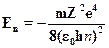
При п 
1 получаем отсюда квантовую частоту перехода 
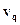между со-седними уровнями:
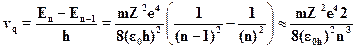
Выражая квантовое число п через энергию уровня, находим
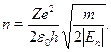
Подставляя это выражение в формулу для квантовой частоты переходамежду соседними высоко лежащими уровнями, приходим к окончатель-ному результату
На этой частоте должен излучать сильно возбужденный атом Бора. Срав-нивая классическую частоту с квантовой , убеждаемся, чтопри той же энергии электрона они совпадают. Это свойственно не тольководородоподобному атому. Аналогичный результат получается для бес-конечной потенциальной ямы, этот же вывод можно сделать и для прочихсистем. Следовательно, соблюдается принцип Бора, и классическая ме-ханика действительно является предельным случаем квантовой.
Задача 30.22.Используя формулы и данные задачи 30.21., продемон-стрировать справедливость принципа соответствия Бора для молекулазота в сосуде.
Решение.При переходе молекул между уровнями с разностью энергий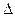 
Е излучается квант света с энергией hv= 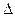Е, откуда находим
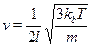
Кроме того, классическая скорость молекул азота равна v=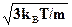 
и они пролетают сосуд от стенки до стенки и обратно за время 
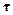= 2l/v
30.7. Отражение и туннелирование частиц
143
(период классического движения). Обратная величина есть классическаячастота
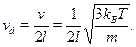
Именно на этой частоте классическая физика предсказывает электромаг-нитное излучение. Принцип соответствия Бора заключается в том, чтосовпадают обе частоты, квантовая (при переходах между высоковозбу-жденными состояниями) и классическая. То же самое справедливо, какмы видели, для атома Бора. Если подставить численные значения, тодля частоты излучения в данной задаче получится величина v ? 3.7кГц, что соответствует длине волны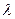 
= с/v ? 80 км --- сверхдлинныерадиоволны. ¦
• Отражение и туннелирование частиц
До сих пор мы имели дело с задачами на связанные состояния. Рассмо-трим теперь примеры инфинитного движения частиц, когда они могутуходить на бесконечно большие расстояния. В простейшем случае дви-жения вдоль одной из координатных осей задача рассеяния частиц сво-дится к задаче взаимодействия частицы с неким потенциальным барье-ром. Мы рассмотрим несколько типов барьеров простой прямоугольнойформы, чтобы усвоить характерные особенности этого типа квантовыхявлений.
Дата добавления: 2016-01-26; просмотров: 2017;