Лекция 11. Линейный гармонический осциллятор. При достаточно малых отклонениях от положения равновесия колебания являются гармоническими

При достаточно малых отклонениях 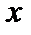от положения равновесия 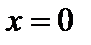колебания являются гармоническими 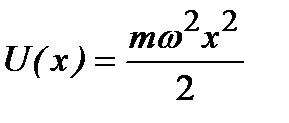. (2.38)

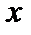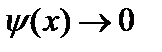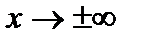Согласно (2.38), значения могут быть бесконечно большими. Это значит, что для волновой функции необходимо выбирать естественное граничное условие: при . (2.39)

Обозначая 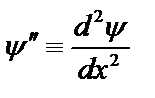и вводя также обозначения: 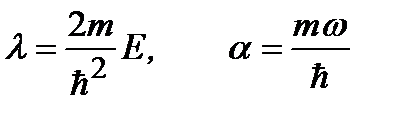, (2.39a)

запишем уравнение Шредингера (2.11) с потенциальной энергией (2.38) в виде:

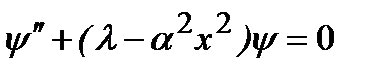. (2.40)

Решение этого уравнения, удовлетворяющее условию (2.39), ищут в виде:

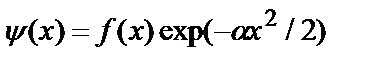, (2.41)

где функцию 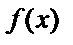необходимо найти. Подставляя (2.41) в (2.40), получаем уравнение

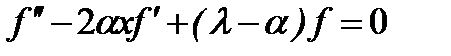. (2.42)

Решение уравнений такого типа ищут в виде ряда , (2.42a)где 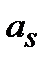– постоянные коэффициенты. этот ряд расходится, растет быстрее, чем 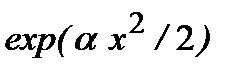. Это значит, что волновая функция (2.41) также расходится. Это противоречит естественному граничному условию. Для существования волновой функции необходимо потребовать, чтобы функция 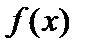в (2.42а) представляла собой не бесконечный ряд, а полином степени 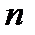. Тогда функция (2.41) будет убывать при 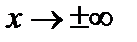. Итак, допустим, что ряд (2.42а) является полиномом степени 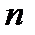. В этом случае отличны от нуля коэффициенты 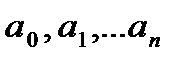, а все другие коэффициенты 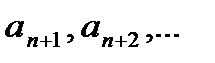должны обращаться в нуль. необходимо, чтобы выполнялось условие 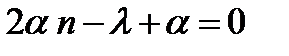.Получаем формулу для энергетического спектра гармонического осциллятора 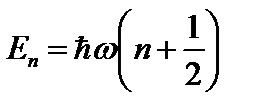(2.43)

В основном состоянии энергия 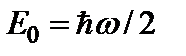. Это энергия нулевых колебаний.

Значениям энергии отвечают собственные функции 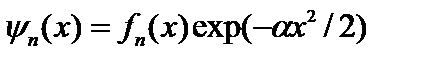. (2.44)

Полиномы 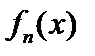, удовлетворяющие уравнению (2.42), называются полиномами Чебышева–Эрмита. Их обозначают как 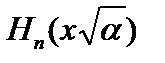: 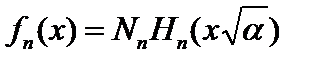. (2.44a)

Здесь 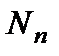– постоянная нормировки. Полиномы Чебышева–Эрмита определяются формулой:

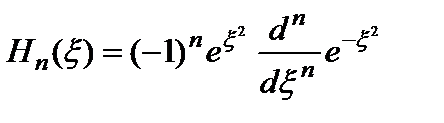. (2.44б)

Из условия нормировки 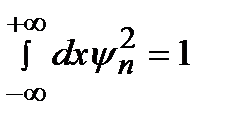следует .

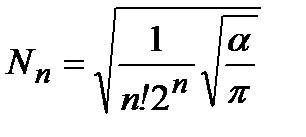Плотность вероятности найти квантовый осциллятор в 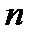-ом состоянии в интервале от 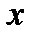до 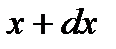равна: 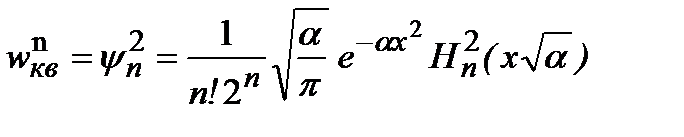. (2.45)

В качестве классического осциллятора рассмотрим математический маятник. Вероятность пребывания этой точки вблизи некоторого положения определяется относительным временем пребывания к периоду колебаний: 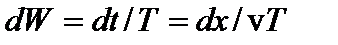.Плотность вероятностей для классического осциллятора обратно пропорциональна его скорости: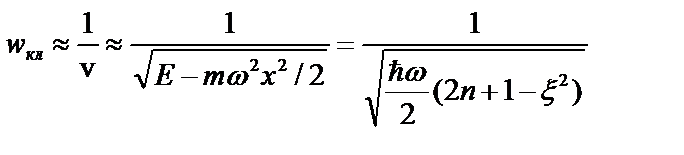

Здесь 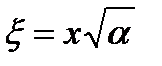. Сопоставим классическую и квантовую плотности вероятностей, изображая 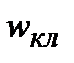пунктирной кривой . Основное состояние: , .

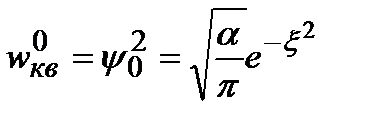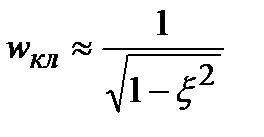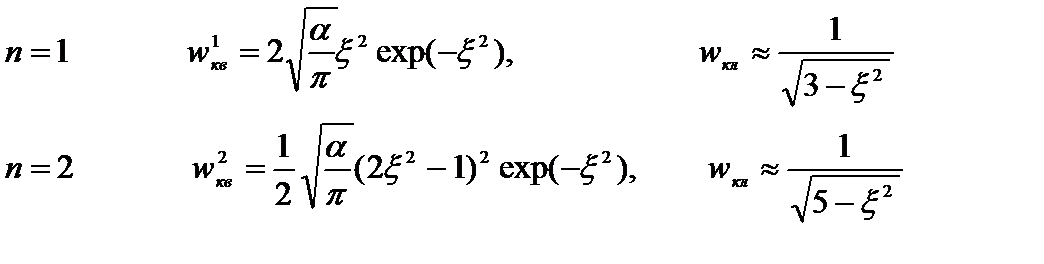
В возбужденных состояниях квантовые и классические вероятности также отличаются друг от друга. Однако с увеличением квантового числа 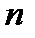количество максимумов квантовых вероятностей возрастает, и в пределе очень больших чисел 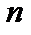огибающая максимумов повторяет характер классической кривой вероятности. В этом проявляется принцип соответствия.

Наличие энергии нулевых колебаний связано с неуничтожимостью движения. Это принципиально отражается в соотношении неопределенностей Гейзенберга. Если бы в основном состоянии осциллятора Е=0, то частица покоится, т.е. ее р=0. Но тогда одновременно можно было бы точно определить также положение частицы.