ГАРМОНИЧЕСКИЙ ТОК В ИНДУКТИВНОСТИ
Пусть через индуктивность L проходит ток i = Imsin(ωt + y).
Электродвижущая сила самоиндукции определяется по формуле (1.3)
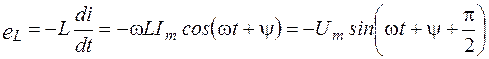 .
.
Значит, напряжение на индуктивности
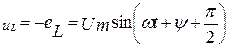
Полученное выражение показывает, что напряжение на индуктивности опережает ток на угол p/2; максимум напряжения смещен влево относительно максимума тока на p/2 (рисунок 2.9). Когда ток проходит через нуль, напряжение достигает положительного или отрицательного максимума, так как оно пропорционально скорости изменения тока (di/dt), которая в момент прохождения тока через нуль максимальна (синусоида тока в этот момент имеет наибольшую крутизну). Когда ток достигает максимума, скорость его изменения, а следовательно, и напряжение на индуктивности обращаются в нуль.

Под фазовым сдвигом j тока относительно напряжения понимается разность начальных фаз напряжения и тока (§ 2.4). Следовательно, в данном случае j = yu- yi= 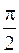 .
.
На векторной диаграмме вектор тока 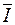 отстает от вектора напряжения
отстает от вектора напряжения 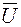 на угол p/2 (рисунок 2.9, в).
на угол p/2 (рисунок 2.9, в).
Амплитуды, так же как и действующие значения напряжения и тока, связаны соотношением, подобным закону Ома
Um = ωLIm = xLIm; U = xLI.
Величина xL= ωL, имеющая размерность сопротивления, называется индуктивным сопротивлением; обратная ей величина 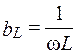 называется индуктивной проводимостью.
называется индуктивной проводимостью.
Итак, Im= bLUm; I = bLU.
Индуктивное сопротивление представляет расчетную величину, с помощью которой учитывается явление самоиндукции.
Мгновенная мощность, поступающая в индуктивность, будет:
рL= u i= UmIm sin(ωt+y+ 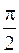 )sin(ωt+y) =
)sin(ωt+y) = 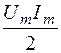 2cos(ωt+y)sin(ωt+y) = = UIsin2(ωt+y) .
2cos(ωt+y)sin(ωt+y) = = UIsin2(ωt+y) .
Она колеблется по синусоидальному закону с угловой частотой 2ω, имея амплитуду UI. Мгновенная мощность в данном случае равна скорости изменения энергии магнитного поля индуктивности (§ 1.3).
Энергия магнитного поля индуктивности согласно формуле (1.4а)
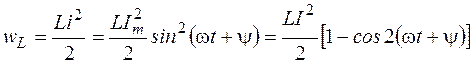
изменяется периодически с угловой частотой 2ω в пределах от 0 до 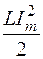 (рисунок 2.10).
(рисунок 2.10).

Поступая от источника, энергия временно запасается в магнитном поле индуктивности, затем возвращается источнику при исчезновении магнитного поля. Энергия магнитного поля достигает максимума в момент перехода тока в индуктивности через амплитудное значение, затем она убывает и обращается в нуль при токе, равном нулю.
Таким образом, происходит колебание энергии между источником и индуктивностью, причем средняя мощность, поступающая в индуктивность, равна нулю. Так как максимальное значение энергии, запасаемой в магнитном поле, равно wLmax= LI2, то индуктивное сопротивление XL= ωL может быть определено как XL = 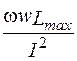 .
.
Дата добавления: 2015-12-16; просмотров: 2255;
