ГАРМОНИЧЕСКИЙ АНАЛИЗ

Во многих случаях моделирование рядов динамики с помощью полиномов или экспонециальной функции не дает удовлетворительных результатов, так как в рядах динамики содержатся заметные периодические колебания вокруг общей тенденции, В таких случаях используют гармонический анализ.

Целью данного анализа являются выявление и измерение периодических колебаний в рядах динамики. Функцию, заданную в каждой точке изучаемого интервала времени, представляют бесконечным рядом синусоидальных и косинусоидальных функций.

Гармонический анализ представляет собой операцию по выражению заданной периодической функции в виде ряда Фурье по гармоникам разных порядков. Каждый член ряда представляет собой слагаемое постоянной величины с функциями синусов и косинусов определенного периода.

Аппроксимация динамики экономических явлений рядом Фурье состоит в выборе таких гармонических колебаний, наложение которых друг на друга (сумма) отражало бы периодические колебания фактических уровней динамического ряда. С помощью рядов Фурье представляют динамику явлений в виде некоторой функции во времени, в которой слагаемые расположены по убыванию периодов:

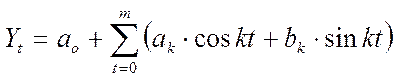
Параметры уравнений рассчитываются методом наименьших квадратов:

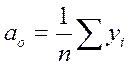
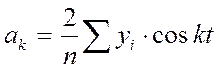
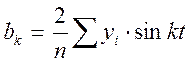
На графиках представлены возможные варианты зависимостей результативного признака Y от факторного Х, где Х – фактор времени