Если автокорреляции в ряду нет, то значения критерия d колеблются вокруг 2.

Эмпирическое значение d сравнивается с табличным значением.

В таблице есть два значения критерия – d₁ и d₂, v и n, где:

d₁ и d₂ -нижняя и верхняя границы теоретических значений;

v -число факторов в модели;

n -число членов временного ряда.

Если 1) d < d₁ - в ряду есть автокорреляция;

2) d > d₂ - автокорреляции нет;

3) d₁ ≤ d ≤ d₂- необходимо дальше исследовать автокорреляцию.

Если в рядах динамики имеется автокорреляция, то оценки коэффициентов регрессии, полученные методом наименьших квадратов, будут несмещенными, но неэффективными, так как наличие автокорреляции увеличивает дисперсии коэффициентов регрессии. Это затрудняет построение доверительных интервалов для коэффициентов регрессии и проверку их значимости.

Из этого следует сделать вывод, что прежде чем проводить коррелляционно-регрессионый анализ временных рядов, необходимо исключить из исследуемых рядов автокорреляцию.

Пример

Осуществите проверку ряда на автокорреляцию на основе критерия Дарбина-Уотсона.

Решение

Для проверки автокорреляции на основе критерия Дарбина-Уотсона в уровнях ряда выдвигается гипотеза о наличии автокорреляции, которая проверяется с помощью случайной величины d.

Период времени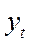
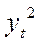
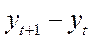
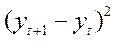
	4,1	16,81	-0,9	0,81
	3,2	10,24	1,1	1,21
	4,3	18,49	-1
	3,3	10,89	1,3	1,69
	4,6	21,16	-1,3	1,69
	3,3	10,89	1,4	1,96
	4,7	22,09	-1,1	1,21
	3,6	12,96	0,5	0,25
	4,1	16,81	0,4	0,16
	4,5	20,25	-0,5	0,25
			0,8	0,64
	4,8	23,04	-0,9	0,81
	3,9	15,21	0,8	0,64
	4,7	22,09	-0,5	0,25
	4,2	17,64
		254,57		12,57

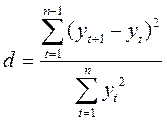=12,57/254, 57=0,049

Полученное значение d сравнивается с табличным значением (см. Приложение).

d₁=1,08, d₂=1,36 => d < d₁, что говорит о наличии автокорреляции в данном ряду.

Приложение