ГАРМОНИЧЕСКИЙ ТОК В ЕМКОСТИ
Пусть напряжение на емкости C синусоидально u = Umsin(wt+y).
На основании (1.8)
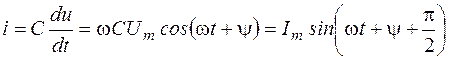 (2.14)
(2.14)
Изменение электрического заряда происходит по косинусоидальному закону в соответствии с приложенным напряжением и. При этом попеременное накапливание положительных и отрицательных электрических зарядов на пластинах емкости обусловливает прохождение в цепи гармонического тока i. Его величина определяется скоростью изменения заряда на емкости (dq/dt).
Выражение (2.14) показывает, что ток i опережает приложенное напряжение и на угол p/2 (рисунок 2.11). Нулевым значениям тока соответствуют максимальные (положительные или отрицательные) значения напряжения и. Физически это объясняется тем, что, когда электрический заряд q и соответственно напряжение и = q/С достигают максимального значения (положительного или отрицательного), ток i равен нулю.

Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т.е.
j = yu- yi=- 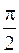 .
.
Таким образом, в отличие от цепи с индуктивностью, где j = p/2, фазовый сдвиг тока относительно напряжения в случае емкости отрицателен (j = −p/2).
На векторной диаграмме вектор тока 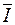 опережает вектор напряжения
опережает вектор напряжения 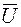 на угол p/2 (рисунок 2.11, в).
на угол p/2 (рисунок 2.11, в).
Амплитуды и соответственно действующие значения напряжения и тока связаны соотношением, подобным закону Ома:
Um= 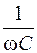 Im; Im = XCIm; U = XCI.
Im; Im = XCIm; U = XCI.
Величина XC= 1/ωС, имеющая размерность сопротивления, называется емкостным сопротивлением. Обратная ей величина bC= ωC называется емкостной проводимостью. Следовательно, Im=bCUm, I=bCU.
Мгновенная мощность, поступающая в емкость,
рC = ui = UmImsin(ωt+y)sin(ωt+y+ 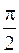 ) = UIsin2(ωt+y),
) = UIsin2(ωt+y),
колеблется синусоидально с угловой частотой 2ω, имея амплитуду, равную UI.
Мгновенная мощность, поступающая в емкость, равна скорости изменения энергии электрического поля емкости.
Энергия электрического поля емкости согласно (1.8а)
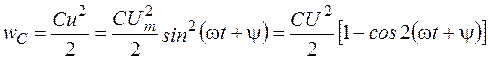
изменяется периодически с угловой частотой 2w в пределах от 0 до 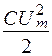 (рисунок 2.12).
(рисунок 2.12).

Поступая от источника, энергия временно запасается в электрическом поле емкости, а затем возвращается к источнику при исчезновении электрического поля. Энергия электрического поля достигает максимума при максимальном значении напряжения на емкости. Затем она убывает и обращается в нуль при напряжении, равном нулю.
Таким образом, так же как и в случае индуктивности, происходит колебание энергии между источником и емкостью, причем средняя мощность Р = 0.
Так как максимальное значение энергии, запасаемой в электрическом поле, равно WCmax= CU2, то емкостное сопротивление XC= 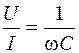 может быть определено как XC=
может быть определено как XC= 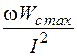 .
.
2.8. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L, С
При прохождении гармонического тока i = Imcosωt через электрическую цепь, состоящую из последовательно соединенных элементов R, L, С (рисунок 2.13), на зажимах этой цепи создается гармоническое напряжение, равное алгебраической сумме гармонических напряжений на отдельных элементах (второй закон Кирхгофа):
и = uR+ иL+ uC.

Напряжение uRна сопротивлении R совпадает по фазе с током i, напряжение uLна индуктивности L опережает, а напряжение иCна емкости С отстает от i на p/2 (рисунок 2.14).

Следовательно, напряжение и на зажимах всей цепи равно:
u = Umcos(ωt + j) = RImcosωt + wLImcos(ωt + 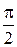 ) +
) +
+ 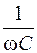 Imcos(ωt-
Imcos(ωt- 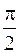 ) = RImcosωt+(wL-
) = RImcosωt+(wL- 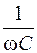 )Imcos(ωt+
)Imcos(ωt+ 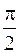 )(2.15)
)(2.15)
Уравнение (2.15) представляет тригонометрическую форму записи второго закона Кирхгофа для мгновенных значений напряжений. Входящая в него величина Х =ХL- ХC= ωL - 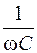 называется реактивным сопротивлением цепи, которое в зависимости от знака может иметь индуктивный (Х > 0) или емкостный (Х < 0) характер. В отличие от реактивного сопротивления Х активное сопротивление R всегда положительно.
называется реактивным сопротивлением цепи, которое в зависимости от знака может иметь индуктивный (Х > 0) или емкостный (Х < 0) характер. В отличие от реактивного сопротивления Х активное сопротивление R всегда положительно.
Для нахождения U и φ воспользуемся векторной диаграммой, соответствующей уравнению (2.15). На рисунке 2.15, а показан случай, когда Х > 0, и на рисунке 2.15, б случай; когда Х < 0.

Падение напряжения от тока в активном и реактивном сопротивлениях изображается катетами прямоугольного треугольника напряжения 0аb, гипотенуза которого изображает напряжение на зажимах цепи. Отсюда
U = 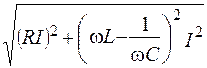
или 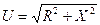 .I
.I
Полученное выражение показывает, что действующие значения (так же, как и амплитуды) напряжения на зажимах цепи и тока, проходящего через данную цепь, связаны соотношением, аналогичным закону Ома:
U = zI; Um = zIm,
где величина z = 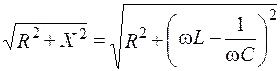 (2.16)
(2.16)
называется полным сопротивлением рассматриваемой цепи.
Активное, реактивное и полное сопротивления относятся к числу основных понятий, применяемых в теории электрических цепей. Из векторных диаграмм следует, что угол фазового сдвига тока i относительно напряжения и равен:
 . (2.17)
. (2.17)
Если задано напряжение u = Umcos(ωt+y) на зажимах цепи с последовательно соединенными R, L и С, то ток определяется по формуле i = 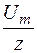 cos(ωt+y-j)Угол φ, равный разности начальных фаз напряжения и тока, отсчитывается по оси ωt в направлении от напряжения к току и является углом острым., прямым или равным нулю |j|
cos(ωt+y-j)Угол φ, равный разности начальных фаз напряжения и тока, отсчитывается по оси ωt в направлении от напряжения к току и является углом острым., прямым или равным нулю |j| 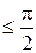 .
.
Угол j положителен при индуктивном характере цепи, т.е. при Х > 0; при этом ток отстает по фазе от напряжения, и φ отсчитывается в положительном направлении: на временной диаграмме вправо от напряжения к току (рисунок 2.16, а), а на векторной диаграмме против хода часовой стрелки от тока 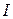 к напряжению U (рисунок 2.15, а).
к напряжению U (рисунок 2.15, а).
Угол j отрицателен при емкостном характере цепи, т.е. при X < 0,при этом ток опережает по фазе напряжение, и φ отсчитывается в отрицательном направлении: на временной диаграмме влево от напряжения к току (рисунок 2.16, б), а на векторной диаграмме - по ходу часовой стрелки от тока I к напряжению U (рисунок 2.15, б).

Итак, следует всегда помнить, что угол j положителен при отстающем и отрицателен при опережающем токе. На временной диаграмме угол отсчитывается от напряжения к току, а на векторной диаграмме - от тока к напряжению.
Ток совпадает с напряжением по фазе при X = XL - xC= 0, т.е. при равенстве индуктивного и емкостного сопротивлений. Такой режим работы электрической цепи называется резонансом напряжений (гл. 7).
Из выражений (2.16) и (2.17) следует, что активное и реактивное сопротивления цепи связаны с полным сопротивлением формулами:
R = zcosj; x = zsinj. (2.18)
Умножив правые и левые части выражений (2.18) на действующее значение токаI, получим действующие значения напряжений на активном и реактивном сопротивлениях, изображаемые катетами треугольника напряжений и называемые активной и реактивной составляющими напряжения:
Ua = RI = zcosjI = Ucosj,
Up = XI = zsinjI = Usinj. (2.19)
Мгновенные значения напряжений на активном и реактивном сопротивлениях, суммирующиеся алгебраически в соответствии с (2.15), имеют фазовый сдвиг p/2. Поэтому непосредственное сложение действующих значений этих функций не дает действующего значения напряжения на всей цепи; как видно из треугольника напряжений и уравнений (2.19), активная и реактивная составляющие напряжения связаны с действующим значением суммарного напряжения формулой
U = 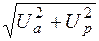 .
.
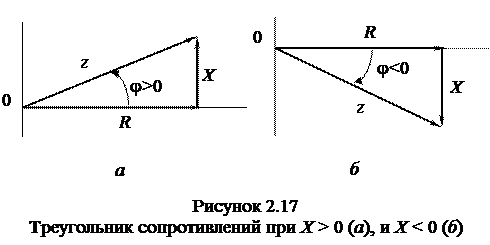
Если все стороны треугольника напряжений разделить на I, то получится прямоугольный треугольник сопротивлений, подобный треугольнику напряжений (рисунок 2.17, а, б).
Треугольник сопротивлений представляет геометрическую интерпретацию уравнений (2.16) и (2.17). Его положение не зависит от начальных фаз напряжения и и тока i: сопротивление R откладывается по горизонтальной оси вправо (в положительном направлении), а реактивное сопротивление X в зависимости от его знака откладывается вверх (X > 0) или вниз (X < 0). Угол j в треугольнике сопротивлений отсчитывается от катета R к гипотенузе z, что соответствует отсчету в треугольнике напряжений от Uа = RI к U = zI.
Для характеристики индуктивных катушек, представляемых цепью с последовательным соединением активного и индуктивного сопротивлений, пользуются понятием добротности катушки QL= XL/R, которое равнозначно тангенсу угла сдвига фаз j для катушки. Чем меньше сопротивление R, тем выше при прочих равных условиях добротность катушки.
Добротность индуктивных катушек, применяемых в диапазоне частот от 1 кГц до 100 МГц, обычно составляет QL= 50…500.
2.9. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕR, L, С
Если к зажимам электрической цепи, состоящей из параллельно соединенных элементов R, L, С (рисунок 2.18), приложено гармоническое напряжение u = Umcosωt, то гармонический ток, проходящий через эту цепь, равен алгебраической сумме гармонических токов в параллельных ветвях (первый закон Кирхгофа): i = iR+ iL+ iC.

Ток iRв сопротивлении R совпадает по фазе с напряжением и, ток iLв индуктивности L отстает, а ток iCв емкости С опережает напряжение на p/2 (рисунок 2.19).
Следовательно, суммарный ток i в цепи равен
i = Imcos(ωt - j) =  Umcosωt +
Umcosωt + 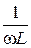 Umcos(ωt -
Umcos(ωt - 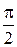 ) +
) +
+ ωСUmcos(ωt + 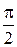 ) =
) =  Umcosωt + (
Umcosωt + ( 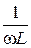 - ωC)Umcos(ωt -
- ωC)Umcos(ωt - 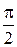 ).(2.20)
).(2.20)

Уравнение (2.20) представляет собой тригонометрическую форму записи первого закона Кирхгофа для мгновенных значений токов. Входящая в него величина b = bL - bC = 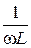 - wC называется реактивной проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b > 0) или емкостный (b < 0) характер. В отличие от реактивной проводимости b активная проводимость g = l/R всегда положительна.
- wC называется реактивной проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b > 0) или емкостный (b < 0) характер. В отличие от реактивной проводимости b активная проводимость g = l/R всегда положительна.
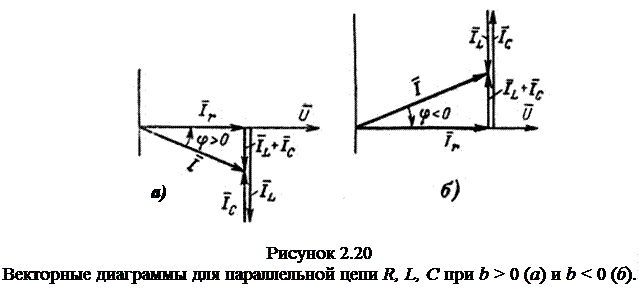
Для нахождения Im и j воспользуемся векторной диаграммой, соответствующей уравнению (2.20) (рисунок 2.20, а и б). Прямоугольный треугольник с катетами IR и [IL+IC] и гипотенузой I называется треугольником токов. Треугольник токов построен на рисунке 2.20, а для b >0, а на рисунке 2.20, б − для b < 0.
Из треугольника токов следует, что 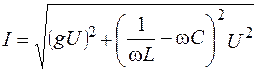 или I = yU; Im=yUm
или I = yU; Im=yUm
Здесь 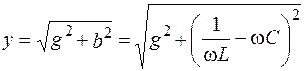 (2.21)
(2.21)
полная проводимость рассматриваемой параллельной цепи.
Активная, реактивная и полная проводимости относятся к числу основных понятий, применяемых в теории электрических цепей.
Угол фазового сдвига тока i относительно напряжения и равен:
j = arctg 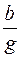 = arctg
= arctg 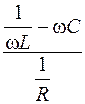 . (2.22)
. (2.22)
Если задано напряжение и = Umcos(ωt + y) на зажимах цепи с параллельно соединенными R, L и С, то ток определяется по формуле
i = yUmcos(ωt + y - j).
Угол j, как и в предыдущем случае, отсчитывается на временной диаграмме ωt от напряжения к току, а на векторной диаграмме - от тока к напряжению; он является острым или прямым углом
|j| 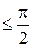 .
.
Угол j положителен при индуктивном характере цепи, т.е. при b > 0; при этом ток отстает по .фазе от напряжения. Угол j отрицателен при емкостном характере цепи, т.е. при b < 0; при этом ток опережает по фазе напряжение. Ток совпадает с напряжением по фазе при b = bR - bC = 0, т.е. при равенстве индуктивной и емкостной проводимостей. Такой режим работы электрической цепи называется резонансом токов.
Из (2.21) и (2.22) следует, что активная и реактивная проводимости цепи связаны с полной проводимостью формулами:
g = ycosj; b = уsinj. (2.23)
Умножив правые и левые части выражений (2.23) на действующее значение напряжения U, получим действующие значения токов в ветвях с активной и реактивной проводимостями изображаемые катетами треугольника токов и называемые активной и реактивной составляющими тока:
| Ia = gU = ycosjU = Icosj; | (2.24) | |
| Ip = bU = ysinjU = Isinj. | ||
Как видно из треугольников токов и уравнений (2.24), активная и реактивная составляющие тока связаны с действующим значением суммарного тока формулой
I = 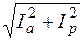 .
.
Разделив стороны треугольника токов на U, получим прямоугольный треугольник проводимостей, подобный треугольнику напряжений (рисунок 2.21, а, б).

Треугольник проводимостей служит геометрической интерпретацией уравнений (2.21) и (2.22); активная проводимость g откладывается по горизонтальной оси вправо, а реактивная проводимость b в зависимости от ее знака откладывается вниз (b > 0) или вверх (b < 0). Угол j в треугольнике проводимостей отсчитывается, от гипотенузы у к катету g, что соответствует отсчету j в треугольнике токов от I = yU к Ia = gU.
Для характеристики конденсаторов, представляемых цепью с емкостной и активной проводимостями, применяется понятие добротность конденсатора QC = b/g = ωCR, которое равнозначно тангенсу угла |j| конденсатора. Обратная величина называется тангенсом угла диэлектрических потерь конденсатора tgd = l/QC (угол диэлектрических потерь d дополняет угол |j| до 90°).
Чем больше сопротивление R, тем больше (при прочих равных условиях) добротность конденсатора и тем меньше угол потерь.
Добротность конденсаторов для разных частот и диэлектриков колеблется в широких пределах, примерно от 100 до 5000. Слюдяные конденсаторы обладают большей добротностью, чем керамические.
Добротность конденсаторов, применяемых в высокочастотной технике, примерно в 10 раз превышает добротность индуктивных катушек.
Дата добавления: 2015-12-16; просмотров: 2760;
