Взаимная индуктивность в электрических цепях. Линейный трансформатор

Электрические цепи могут содержать контуры (два или более), в которых магнитный поток одного из них пронизывает другой, например, в случае двух и более параллельных линий электропередачи. Это явление называется взаимной индукцией между контурами. Если магнитный поток изменяется во времени, то в магнитосвязанных контурах наводятся ЭДС, например, ЭДС в 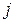- том контуре при изменении тока и пропорционального ему магнитного потока в 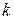- том определяется по формуле

,

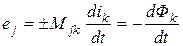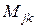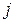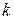где - коэффициент взаимной индукции или взаимная индуктивность между контурами и , характеризует тесноту связи (коэффициент связи) между контурами. Необходимо отметить, что в электрических цепях всегда 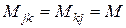. С увеличением расстояния между контурами 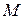уменьшается. Взаимная индуктивность 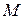, как и собственная индуктивность 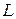, измеряется в генри (Гн).

Знаки «+» и «–» перед 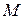означают, что выполнении расчётов цепей необходимо знать не только величину 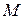, но и её знак, который зависит от взаимного расположения контуров; так как магнитные потоки в контуре, наводимые собственным током и током взаимного контура могут по направлению либо совпадать, либо не совпадать. В связи с этим различают согласное и встречное включение контуров (или обмоток катушек). Для определения знака, с которым добавляется потокосцепление (или поток) взаимной индукци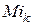и (или 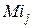) к потокосцеплению самоиндукци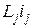и (или 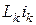), необходимо разметить зажимы ветвей, содержащих индуктивно связанные элементы. Обычно один из зажимов первой ветви произвольно принимают за начало и наносят около него точку; вторая точка ставится у зажима второй ветви так, чтобы магнитное потокосцепление обоих индуктивных элементов увеличивалось бы вследствие взаимной индукции, когда ток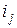и и 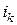одинаково направлены относительно отмеченных зажимов своих элементов (рис.8.15).

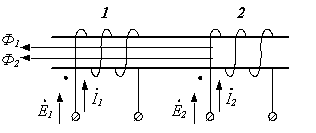
Рисунок 8.15. Согласное включение обмоток

Для установившегося синусоидального режима последнее выражение может быть записано для комплексных амплитуд .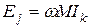

Если поток (потокосцепление) сцеплён только со своей обмоткой, то такой поток называется потоком рассеяния, а соответствующая ему индуктивность называется индуктивностью рассеяния. Величины, характеризующие рассеяние обозначаются индексом .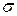

Трансформатор в простейшем случае представляет собой две индуктивно связанные обмотки при сильной связи между ними; для этого они должны быть, надеты на общий ферромагнитный магнитопровод (сердечник). Практическое значение трансформаторов заключается, прежде всего, в возможности изменения величин напряжения. При сильной связи между обмотками почти одинаковый поток 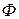пронизывает каждый из витков, поэтому ЭДС, индуктируемые в обмотках, пропорциональны числам витков 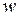обмоток. Если к первой (первичной) обмотке с числом витков 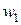приложить напряжение 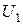, то напряжение 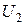на зажимах второй (вторичной) обмотки с числом витков 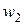можно определить по формуле

.

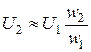Отношение вторичного напряжения к первичному напряжению называется коэффициентом трансформации 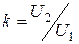. Если 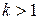, то трансформатор называется повышающим, если 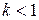- понижающим.

Трансформатор, не имеющий потерь в магнитопроводе в проводах обмоток, называется идеальным. Для идеального трансформатора коэффициент трансформации можно определить как отношение чисел витков обмоток

.

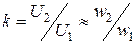Кроме того, трансформатор изолирует первичную и вторичную обмотки в электрическом отношении, сохраняя возможность передачи энергии между обмотками.

Ферромагнитный сердечник может привести к нелинейной зависимости между первичным и вторичным напряжениями. Здесь мы ограничимся анализом работы трансформатора лишь в линейном режиме, когда все потокосцепления прямо пропорциональны токам и могут быть выражены через собственные и взаимные индуктивности, величины которых не зависят от тока. В таком режиме работают измерительные трансформаторы и трансформаторы в системах сигнализации, связи, радиотехнической и телевизионной аппаратуре. В режиме близком к линейному работают силовые трансформаторы в энергосистемах; нелинейность их параметров проявляется практически только в режиме холостого хода и некоторых анормальных режимах.

Основные уравнения и векторная диаграмма линейного трансформатора. Предположим, что первичная обмотка трансформатора подключена и источнику синусоидальной ЭДС 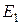. Будем также считать, что числа витков первичной и вторичной обмотки равны 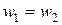, если же 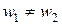, то параметры одной обмотки должны быть приведены ко второй (приведение выполняется через коэффициент трансформации).

Уравнения для первичной и вторичной обмоток запишем на основе второго правила Кирхгофа, используя символический метод (рис.8.16, а).

;

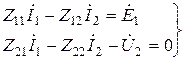где ; ; ;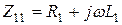

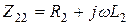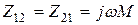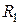и 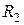- активные сопротивления первичной и вторичной обмоток; 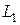, , 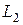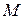- их собственные и взаимная индуктивности соответственно, 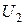- вторичное напряжение, равное напряжению нагрузки.

Рисунок 8.16. Линейный двухобмоточный трансформатор (а) и его Т-образная схема замещения (б)

Для практических расчётов пользуются схемами замещения трансформаторов, в которых магнитная связь между обмотками заменяется электрической. Наиболее часто используется Т-образная схема замещения (рис.8.16, б). Здесь 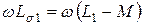и 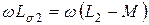- сопротивления рассеяния первичной и вторичной обмоток соответственно, 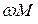- сопротивление ветви намагничивания (в ней протекает ток намагничивания).

Построим качественную векторную диаграмму трансформатора (рис.8.17). Построение начинают с векторов напряжения и тока вторичной цепи, соответственно, 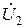и 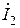. Обычно трансформаторы в электроэнергетических установках имеют активно-индуктивную нагрузку; в этом случае вектор тока 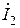отстаёт от вектора напряжения 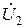на угол 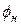, причём 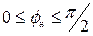. Вектор падения напряжения от вторичного тока на активном сопротивлении 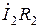совпадает по фазе с вектором тока, а на индуктивном сопротивлении рассеяния 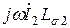- опережает его на 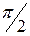. Суммируя геометрически векторы: 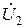, 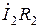и 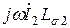получим падение напряжения на ветви намагничивания от тока намагничивания 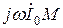. Ток намагничивания равен геометрической разности первичного и вторичного токов

.

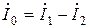Падение напряжения на ветви намагничивания это ЭДС, индуцируемая во вторичной обмотке 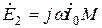,а ток намагничивания отстаёт от неё на 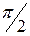. Суммируя геометрически векторы вторичного тока 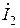и тока намагничивания 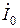получим вектор первичного тока .

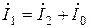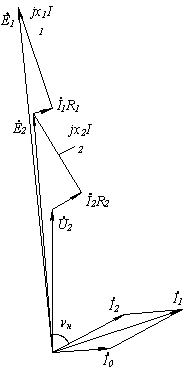
Рисунок 8.17. Векторная диаграмма линейного трансформатора

Падение напряжения от первичного тока на активном сопротивлении 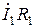совпадает по фазе с вектором тока, а на индуктивном сопротивлении рассеяния 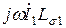- опережает его на 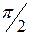. Суммируя геометрически векторы: 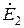, 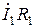и 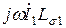получим вектор ЭДС, приложенной к первичной обмотке .

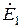8.6. Трёхфазные электрические цепи

Многофазные системы переменных токов впервые были предложены Николой Тесла (1888). Это обеспечило преимущественное развитие энергосистем переменного тока (до Тесла Томас Эдисон создавал энергосистемы постоянного тока). В настоящее время преимущественно используются трёхфазные системы токов.

Трёхфазной электрической цепью называют связную совокупность трёх электрических цепей, в которых действуют синусоидальные ЭДС одной и той же частоты, сдвинутые друг относительно друга по фазе и создаваемые общим источником энергии - трёхфазным генератором. Отдельные цепи, входящие в состав такой цепи, называются фазами и обычно обозначаются буквами A, В, С, а совокупность ЭДС, действующих в этих фазах, а также совокупность токов и напряжений фаз называется трёхфазной системой ЭДС, токов и напряжений. Трёхфазная система ЭДС (токов, напряжений) называется симметричной, если ЭДС (токи, напряжения) всех фаз равны по амплитуде и сдвинуты относительно друг друга по фазе на угол 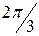, в противном случае трёхфазная система называется несимметричной.

Векторная диаграмма трёхфазной системы ЭДС показана на рис.8.18. Трёхфазная система ЭДС вырабатывается с помощью синхронного трёхфазного генератора.

Рисунок.8.18. Трёхфазная система ЭДС

Трёхфазная система с одной стороны является более экономичной по числу используемых проводников – их три (в двухфазной системе Тесла использовалось четыре провода), с другой стороны – позволяет реализовать простые по конструкции, следовательно, надёжные и дешёвые электрические двигатели – основные потребители электрической энергии (с помощью трёхфазной системы токов создаётся вращающееся магнитное поле, впервые описали Тесла и Феррарис).

На электрической схеме трёхфазный генератор принято изображать в виде трёх обмоток, расположенных под углом 120°. Обмотки генератора могут быть соединены звездой или треугольником.

При соединении звездой одноимённые зажимы трёх обмоток объединяют в одну точку (рис.8.19,а), которую называют нулевой точкой генератора 0. Обмотки генератора обозначают буквами А, В, С.

При соединении обмоток генераторов треугольником (рис.8.19,б) конец первой обмотки соединяют с началом второй, конец второй – с началом третьей, конец третьей – с началом первой. Геометрическая сумма ЭДС в замкнутом треугольнике равна нулю, поэтому если к зажимам генератора А, В, С нагрузка не присоединена, то ток по обмоткам генератора протекать не будет.

.

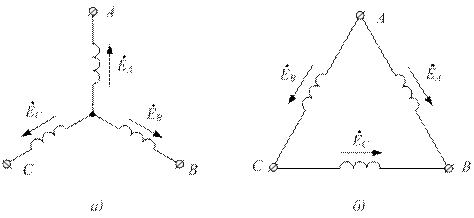
Рисунок 8.19. Соединение обмоток трёхфазного генератора в звезду (а) и треугольник (б)

Пять возможных способов соединения трёхфазного генератора показаны на рис.8.20.

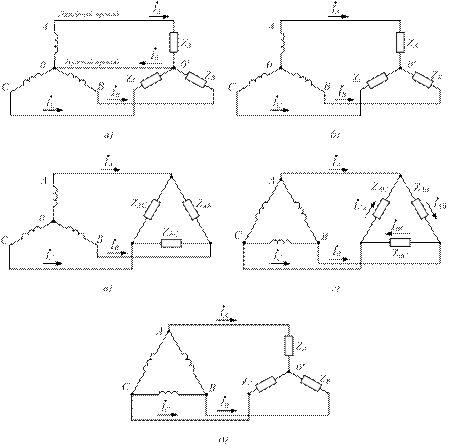
Рисунок 8.20. Схемы соединения обмоток в трёхфазных цепях

Точку, в которой объединены три конца трёхфазной нагрузки при соединении её звездой, называют нулевой точкой нагрузки и обозначают 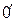. Ток нулевого провода 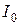имеет положительное направление от точки 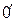к 0. Схемы на рис.8.20 называют: а) звезда-звезда с нулевым проводом, б) звезда-звезда без нулевого провода, в) звезда-треугольник, г) треугольник-треугольник, д) треугольник-звезда.

Напряжения между линейными проводами называют линейными и обозначают, например, 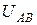(линейное напряжение между фазами А и В); модуль линейного напряжение – .

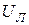Токи в линейных проводах называют линейными, их обозначают 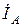, 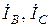. За положительное направление для них принимается направление от генератора к нагрузке. Модули линейных токов обозначают .

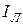Каждую из трёх обмоток генератора называют фазой генератора; каждую из трёх нагрузок – фазой нагрузки; протекающие по ним токи - фазовыми токами генератора 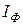или соответственно нагрузки, а напряжения на них – фазовыми напряжениями.

Соотношения между линейными и фазовыми напряжениями и токами. При соединении обмоток генератора в звезду линейное напряжение по модулю в 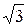раза больше фазового напряжения генератора :

.

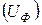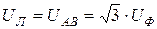Линейный ток 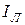при соединении обмоток генератора в звезду равен фазовому току генератора

.

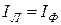При соединении обмоток генератора в треугольник линейное напряжение равно фазовому напряжению

.

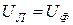При соединении нагрузки в звезду линейный ток равен фазовому ток нагрузки.

При соединении нагрузки в треугольник положительные направления для токов в сторонах треугольника выбирают по часовой стрелке. Индексы у токов соответствуют выбранным для них положительным направлениям: первый индекс для точки, из которой ток вытекает, второй – для точки в которую он втекает

При соединении нагрузки в треугольник линейные токи не равны фазовым токам нагрузки и определяются по первому правилу Кирхгофа

.

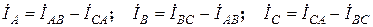Источники ЭДС в трёхфазных цепях являются синусоидальными, поэтому расчёт и исследование процессов в них производится теми же методами, что и однофазных цепей. Для цепей трёхфазного тока также применим символический метод, могут строиться векторные и топографические диаграммы.