Цепи переменного (синусоидального) тока

Синусоидальную ЭДС в любой момент времени можно определить по формуле (в тригонометрической форме)

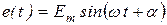, (8.6)

где 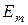- амплитудное значение ЭДС, 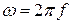- круговая частота, 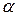- начальная фаза.

Аналогично выражаются и другие синусоидальные величины, например, ток

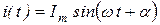. (8.7)

Значения 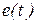, 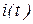называются мгновенными значениями и обозначаются строчными буквами латинского алфавита.

На практике часто синусоидальные величины характеризуются действующими значениями

.

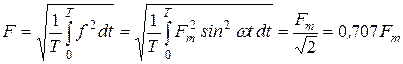Аналогично

, .

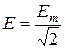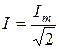Действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток. Действующие и амплитудные значения обозначают прописными буквами. Большинство измерительных приборов показывает действующее значение.

При анализе цепей синусоидального тока часто также пользуются действующими значениями. Так для определения теплового действия тока достаточно знать только его величину. При расчёте взаимодействия двух токов необходимо знать взаимное направление токов.

Для расчётов цепей с синусоидальными источниками ЭДС широко используется символический метод (метод комплексных амплитуд, комплексный метод), введённый в электротехнику инженерами Кеннели и Штейнметцом (1893-1894 гг.). Этот метод основан на представлении гармонических функций в виде проекций вращающихся векторов на комплексной плоскости. Так синусоидальный ток 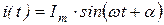может быть представлен мнимой частью 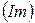вектора 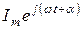, т.е.

.

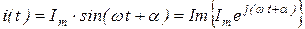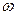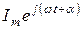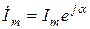Так как скорости вращения векторов определяются круговой частотой , которая для всех векторов одинакова, поэтому все векторы являются неподвижными друг относительно друга, что является основанием для построения векторных диаграмм, при этом вектор равен , где 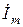– комплексная величина. Таким образом, синусоидальные токи и напряжения могут быть представлены неподвижными векторами 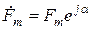, направление которых определяется начальной фазой 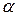, а длина амплитудой. При этом операция взятия производной от действительной функции заменяется умножением на 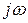её комплексного изображения, а операция интегрирования действительной функции заменяется делением на 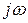её комплексного изображения. Таким образом, комплексный метод является элегантным методом алгебраизации дифференциальных уравнений. Уравнения по первому и второму правилам Кирхгофа будут не дифференциальными, а алгебраическими – аналогичными уравнениям для цепи постоянного тока, что существенно упрощает их решение.

Совокупность векторов токов и напряжений, построенных для электрической цепи, называется векторной диаграммой. Векторные диаграммы широко используются в электроэнергетике при выполнении расчётов и анализе поведения различных электроустановок.

Если в электрическую цепь включены только источники с синусоидальными ЭДС и/или токами, то уравнения связи между напряжениями на элементах и токами в них упрощаются по сравнению с выражениями (8.1) – (8.3).

Если к активному сопротивлению приложено синусоидальное напряжение 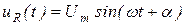, ток через сопротивление также будет синусоидальным

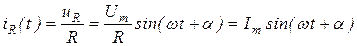. (8.8)

В соответствии с (8.8) ток имеет ту же начальную фазу 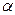, что и напряжение (рис.8.6).

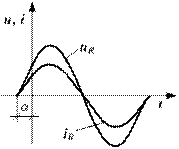
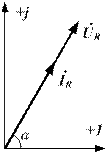
Рисунок 8.7. На активном сопротивлении Рисунок 8.8. Векторная диаграмма тока и ток и напряжение совпадают по фазе напряжения для активного сопротивления

Из (8.8) также следует, что 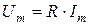и 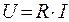. Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам

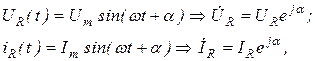
и поделив первый комплекс на второй, получим

.

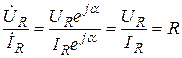Векторная диаграмма тока и напряжения для активного сопротивления представлена на рис.8.8.

Если через индуктивность протекает синусоидальный ток 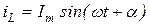, то напряжение на её зажимах

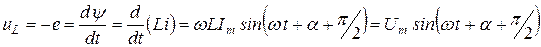. (7.9)

Следовательно, ток в индуктивности отстаёт от напряжения на угол 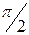(рис.8.9).

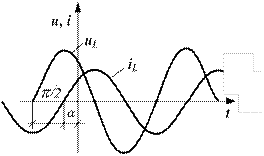
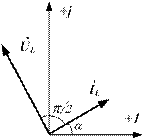
Рисунок 8.9. Ток в индуктивности отстаёт Рисунок 8.10 Векторная диаграмма от напряжения на угол 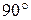тока и напряжения для индуктивности

Из выражения (8.10) следует, что 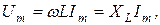где 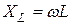– реактивное индуктивное сопротивление катушки; его размерность – Ом. Величина 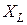линейно зависит от частоты. При 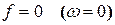, т.е. для постоянного тока 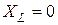, если 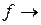¥, то и ¥.

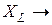Комплексы тока и напряжения имеют вид:

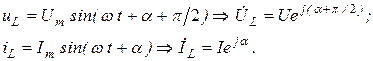
Разделив первый комплекс на второй, получим

,

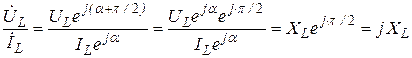или

.

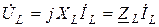Умножение вектора на 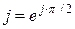соответствует повороту его на угол 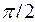в положительном направлении (против часовой стрелки) не изменяя его длины.

Векторная диаграмма тока и напряжения для катушки индуктивности представлена на рис.8.10.

Если к конденсатору приложить синусоидальное напряжение 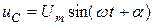, то через него будет протекать ток

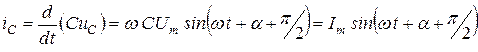. (8.10)

Следовательно, ток в конденсаторе опережает напряжение по фазе на угол 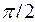(рис.8.11).

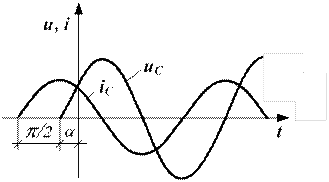
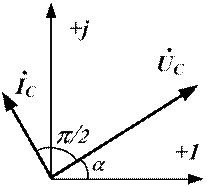
Рисунок 8.11. Ток в конденсаторе опережает Рисунок 8.12. Векторная диаграмма напряжение на угол 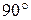тока и напряжения для конденсатора

Из (8.10) следует, что

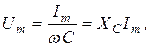
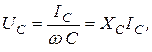
где 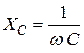– реактивное ёмкостное сопротивление конденсатора; его размерность – Ом.

Величина Х_С с увеличением частоты уменьшается по гиперболическому закону; при 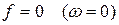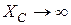, т.е. для постоянного тока конденсатор является разрывом цепи.

Запишем выражения для комплексов напряжения и тока

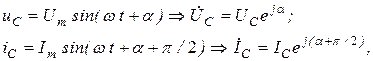
и поделив первый комплекс на второй, получим

,

.

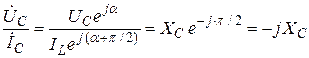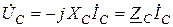Умножение вектора на – 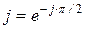означает его поворот его на угол 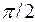в отрицательном направлении (по часовой стрелке) не изменяя длины. Векторная диаграмма для тока и напряжения для конденсатора приведена на рис.8.12.