Частица в бесконечно глубокой потенциальной яме
Потенциал в этой задаче имеет вид:
Такая система соответствует частице, движущейся вдоль прямой линиии отскакивающей от абсолютно отражающих препятствий в точках х = 0и х = l. В область бесконечного потенциала частица проникнуть не мо-жет, следовательно  ?
? 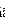 ?
?

(х)=Аsin(kх)+Вcos(кх). Используем сначалапервое граничное условие:
Asin(kx)+Bcos(kx)
или бегущих
Аеiкх+Вei-кх
если 0 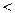 х
х 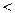 I,если х
I,если х 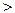 I или х
I или х 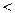 0.
0.
 ?
?  ?
?

(х) = Аsin(кх). Если продолжить нашу аналогию, то можно сказать,что на струне, закрепленной в одной точке, бегущих волн не бывает:отражение от неподвижной точки обязательно порождает стоячую волну.Однако на длину волны никаких ограничений не накладывается: такаяструна также не звучит.
Теперь наложим второе из граничных условий:
 ?
? 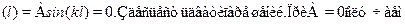 ?
?

(х) = 0, чтоозначает отсутствие частицы в яме (вероятность найти ее всюду равнанулю). Поэтому нас интересует второе решение, когда sin(kl) = 0. Этовозможно лишь при некоторых значениях волнового вектора: kп = 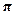 n/1(п = 1, 2, 3,...). Так как энергия частицы связана с волновым вектором,то
n/1(п = 1, 2, 3,...). Так как энергия частицы связана с волновым вектором,то

Мы получили квантование энергии, то есть наша ``струна'', закрепленнаяс обеих сторон, зазвучала, так как появились выделенные частоты.
Подставляя найденные разрешенные значения волнового вектора в вы-ражение для волновой функции, получаем ее в виде:
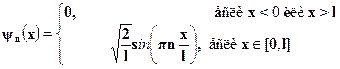
Смысл квантового числа п: оно на единицу больше числа нулей вол-новой функции. Значение постоянной А = у/2/7 определено из условиянормировки (см. задачи в последнем разделе этой главы).
Откуда же берется дискретность уровней энергии, характерная и дляатома? Сравним со свободной частицей: уравнения те же, но с инымиграничными условиями! Здесь возможны две постановки задачи. В пер-вом случае исследуется состояние, которому в классике соответствовалобы инфинитное движение (задача рассеяния). Обычно в таких случаяхрешения возможны при любых значениях энергии Е (как говорят, спектрнепрерывен). Во втором случае исследуется состояние, которому в клас-сикесоответствует финитное движениев ограниченной области про-странства (задача на связанные состояния). Требование конечности вол-новой функции во всем пространстве ведет к квантованию энергии.
Глава 30. Уравнение Шредингера
Подчеркнем: в этом случае стационарное уравнение имеет физическиприемлемые решения не всегда, а лишь при некоторых значениях Е. Какследствие возникает дискретныйспектр энергии системы.
Задача 30.21.Определить разность соседних уровней энергии 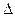 Е длячастицы в бесконечной потенциальной яме при больших значениях п. По-лученный результат использовать для оценки разности соседних уровнеймолекул азота при комнатной температуре Т = 300 К в сосуде. Принятьмассу молекулы т = 2.3 10-26 кг, а линейный размер сосуда l = 0.1 м.Сравнить результат с кинетической энергией поступательного движениямолекул азота.
Е длячастицы в бесконечной потенциальной яме при больших значениях п. По-лученный результат использовать для оценки разности соседних уровнеймолекул азота при комнатной температуре Т = 300 К в сосуде. Принятьмассу молекулы т = 2.3 10-26 кг, а линейный размер сосуда l = 0.1 м.Сравнить результат с кинетической энергией поступательного движениямолекул азота.
Решение.Используя выражение для уровней энергии частицыв потенциальной яме, находим разность энергий соседних уровней
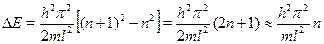
при больших значениях п. Кинетическая энергия поступательного дви-жения молекул азота равна Е = 3 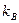 Т/2 ? 6, 21 10-21 Дж. ПриравниваяЕ и выражение для энергии уровней частицы в яме, находим, что такаяэнергия соответствует квантовым числам порядка
Т/2 ? 6, 21 10-21 Дж. ПриравниваяЕ и выражение для энергии уровней частицы в яме, находим, что такаяэнергия соответствует квантовым числам порядка
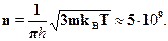
Уже само по себе это число говорит, что мы находимся в области крайневысоких возбуждений, то есть в области справедливости классическихзаконов. Разность соседних уровней получаем, подставляя в формулудля 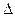 Е найденное выражение для квантового числа п:
Е найденное выражение для квантового числа п:
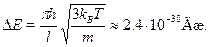
В электронвольтах те же характеристики имеют значения Е 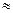 0.039 эВ,
0.039 эВ, 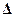 Е
Е 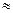 1.5 10-11 эВ. Относительная разность уровней ничтожно мала:
1.5 10-11 эВ. Относительная разность уровней ничтожно мала: 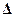 Е/Е
Е/Е 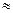 4 10---10, и потому в классической физике квантовой дискретно-стью пренебрегают. ¦
4 10---10, и потому в классической физике квантовой дискретно-стью пренебрегают. ¦
Дата добавления: 2016-01-26; просмотров: 928;
