Высокий бесконечный барьер

Потенциальная энергия имеет тот же вид, но энергия частицы меньшевысоты барьера: Е 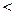U(рис. 30.2). Решение в области 1 остается преж-ним: суперпозиция прямой и отраженной волн. В области же 2 из-заобратного соотношения между энергией частицы и высотой барьера вол-новой вектор становится мнимым:

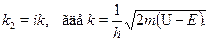
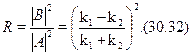
от барьера. Соответственно, величина D = 1 --- R= 4 /( 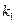+ 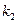)2,

При подстановке мнимого волнового вектора 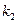= iк в выражение для коэффициента отражения R получаем, что B = 1. Как и в классике,частица с энергией, меньшей высоты бесконечного барьера, наверняка

Глава 30. Уравнение Шредингера

Рис.30.2: Высокий потенциальный барьер

Рис.30.3: Конечный потенциальный барьер

отразится от него. Правда, в классической физике частица вовсе не мо-жет проникнуть под барьер. Наше же решение уравнения Шредингерадля области 2 в случае высокого барьера становится равным

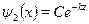
Это уже не совсем волна, а экспоненциально затухающая функция. Каки в случае низкого барьера, отброшено нефизическое решение --- экспо-ненциально растущая функция вида еzх. Под глубиной проникновениячастицы под барьер d принято понимать расстояние, на котором интен-сивность потока (вероятность) ослабевает в е раз. Из выражения для 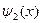следует, что d = 1/(2к).